Випромінювання елемента Гюйгенса (односторонній випромінювач)

З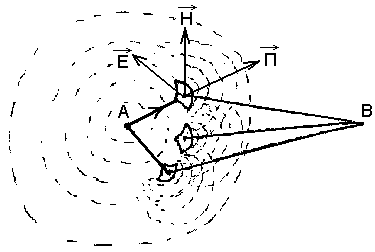 гідно з принципом Гюйгенса: у нас є випромінювач, який випромінює хвилю ; кожний елемент хвилі теж випромінює сферичні хвилі ( їх оживаюча буде наступним фронтом первинного випромінювача):

- дотичні до поверхні (сфери).

Моделлю Гюйгенса може бути сума двох елементарних випромінювачів (електричного і магнітного), які знаходяться під кутом 90 один до одного.

Наша задача : знайти поле, що випромінюється елементом Гюйгенса:

Ц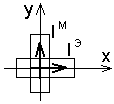 ей розв'язок можна знайти, знаючи крайові умови.

Розглядаємо тепер таку задачу:

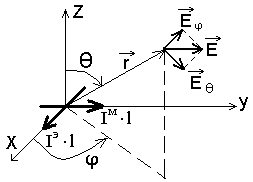- моменти

Постановка задачі: на початку сферичної системи координат є два елементарних випромінювача (по осі у - , по осі х - ).

Знайти поле в дальній зоні.

Задача розв'язується методом суперпозиції двох розв'язків, які нам відомі (будуть складові тільки по  і , r - не буде при r>>).

;

Кожна з цих складових ( і ) буде теж суперпозицією полів від кожного елементарного випромінювача окремо:

Аналогічно для :

В тих розв'язках, що в нас є, необхідно повернути систему координат так, як нам потрібно (тобто записуємо ті розв'язки, що є в новій повернутій системі координат).

Запишемо зразу кінцевий вигляд:

Для H записувати не будемо.

Введемо безрозмірний коефіцієнт:

Винесемо магнітний струм за дужки:

Візьмемо випадок, коли m = 1 :

Знаходимо поле (модуль вектора електричного поля):

Точно так же можна знайти і Н , поставивши перед Z.

kr - це фаза.

- по такому закону змінюється поле в дальній зоні.

- діаграма спрямованості елемента Гюйгенса (нашої антени)

- діаграма спрямованості тільки при m = 1, якщо m  1, то вона буде якась інша.

Будуємо її:

при  = 0 маємо 1

 = 90 маємо 1/2

 = 180 маємо 0

Т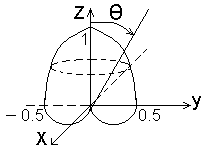 обто форма - кардіоїда. Максимум випромінювання буде  площині XOY (максимум буде  напрямку хвилі):

Всі характеристики елементарного випромінювача (його діаграма направленості і т.д.) використовуються для розрахунку апертурних антен (наприклад, рупорна антена).

П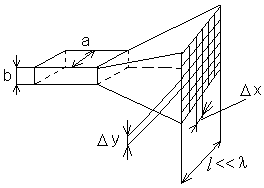 оле в даній точці простору знаходимо як суперпозицію від кожного випромінювача окремо (на які ми розбиваємо апертуру антени так, щоб і ).

Другий приклад: антена для "полювання на лисиць"

Розглянувши всі 3 елементи випромінювача можна зробити висновки про поширення електромагнітного поля в просторі:

1. Напруженість поля пропорційна швидкості зміни струму (тобто частоті)

2. Вектори поля і в дальній зоні спадають по закону і поширюються на далекі відстані (тобто вони існують самостійно у вигляді електромагнітної хвилі)

3. Вектори і завжди взаємно  .

4. Відношення 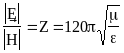, тобто відношення між амплітудами дорівнює хвильовому опору середовища.

5. Діаграма спрямованості : в електричних і магнітних випромінювачах sin, а в елементі Гюйгенса .

6. Швидкість поширення електромагнітних хвиль в просторі залежить від параметрів середовища  і  і дорівнює:

фазова швидкість:

(у вакуумі )

Для будь-якого випромінювача в ізотропному однорідному середовищі сукупність точок, куди приходить хвиля при  = const буде складати сферу:

 = kr = const

r = const

7. Таким чином фронт електромагнітної хвилі, випромінюваної елементарним випромінювачем, в дальній зоні сферичний (r = const). А якщо взяти нескінченно довгий провідник, який складається з багатьох елементарних випромінювачів, з електричним або магнітним струмом:

то ми маємо циліндричні хвилі (бо випромінювання вздовж немає, а є тільки у всі сторони  провіднику).

Якщо взяти нескінченно велику площину, на якій розміщені тісно елементарні випромінювачі (в ній рівномірно розподілені струми), то ми отримаємо плоску хвилю.

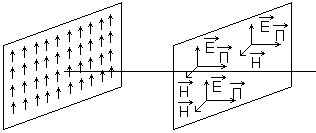Плоскої електромагнітної хвилі - це така хвиля, фронт якої є нескінчена кількість точок з однаковою фазою і вона є безмежною площиною.

Якщо ми маємо до того ж однакові амплітуди і , то ми маємо плоску однорідну електромагнітну хвилю.

Якщо амплітуди і змінюються в площині, то ми маємо плоску неоднорідну електромагнітну хвилю. Енергія поширюється  до площини поширення хвилі (це вектор Пойнтінга). А вектори і лежать в площині поширення цієї плоскої хвилі.