Матерія. Поле. Речовина.

Поле, як і речовина, має масу, момент кількості руху. Тощо.

Світло тисне на пластину, тобто світло має інерційну масу. Світловий промінь притягується масивними космічними тілами, значить світло має гравітаційну масу.

В нашому курсі ми будемо вивчати макроскопічну електродинаміку.

М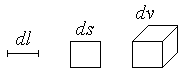 іж атомами в кристалічній решітці існує проміжок, він доволі великий. Приймемо, що dt – період обертання електронів навколо ядра.

Математичний апарат, який ми будимо застосовувати залежить від співвідношення L та , де - довжина хвилі.

Випадки:

1. L<< (теорія кіл з зосередженими параметрами) – розглядаємо по усім

координатам.

2. Вважаємо, що магнітна складова зосереджена в L (індуктивність). А електричне поле – тільки в С (електричним полем навколо С нехтуємо, бо за межами конденсатора воно швидко спадає).

В опорі R відбувається перетворення електромагнітної енергії в теплову.

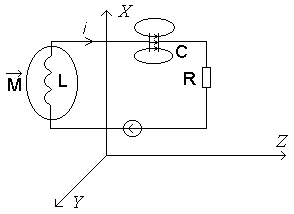
Електричне коло може бути представлене скалярними величинами U_L,U_C,U_R,I.

Будемо вважати, що I_LI_CI_R, тоді струми залежать лише від часу, а від координат не залежать:

I=i(t)

U=u(t)

Якщо L,C,R=const, тоді ми маємо лінійні диференційні рівняння; якщо вони залежать від і та u - нелінійні диференційні рівняння; якщо R,L,C залежать від часу, то це параметричні дифф. рівняння.

1. L_X,Y<< , L_Z  (наприклад довга лінія)

Д вохпровідна довга лінія:

- магнітне поле, в данному випадку воно розподілене, тому індуктивнність L теж розподілена вздовж усієї довжини. .

- електричне поле, розподілена ємність. ,

Провідність між провідниками

Струм і напруга залежать від двох координат:

i=i(z, t)

u=u(z, t)

-тут використовуються дифф. рівняння в часткових похідних (лінійні, нелінійні, параметричні).

2. L_X,Y,Z

Н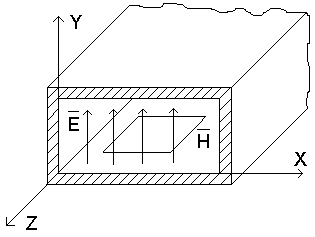 априклад, прямокутний хвилевід:

Тут вводити поняття струму і напруги недоцільно, тому що їх важко поміряти, тому введемо поняття поля. R,L,C розподілені згідно з координатами.

Електричне поле буде максимальне між широкими сторонами. Магнітне поле замикається вздовж ліні передачі.

Струми тут є і вони течуть і вздовж і впоперек.

Максимальне поле в центрі, а мінімальне біля стінок, тобто воно розподілене за синусоїдальним законом:

В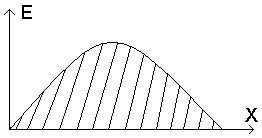 даному випадку немає сенсу вимірювати струм або напругу, доцільніше буде знати тільки поля, які будуть функціями чотирьох координат:

Маємо векторні величини: , .

В математичному апараті маємо такі похідні:

Адекватний математичному аналізу – векторний аналіз.

3. L>> (по усім координатам).

Прикладом такої системи може бути оптичний апарат ( -(довжина хвилі) вимірюється в нанометрах, величина самого приладу набагато більша ніж довжина хвилі).

В важаємо, що елктро-магнітне поле еквівалентно світловим променям:

Основні форми, в яких застосовуються диф. рівняння в мат. аналізі.

Існують фізичні та математичні поля.

Фізичне поле – це простір, в кожній точці якого задана фізична величина (наприклад: електричне поле, магнітне поле, температура, тиск)

Розглянемо математичні (абстрактні) поля:

1. Скалярне поле - в кожній точці задана якась математична величина.

Е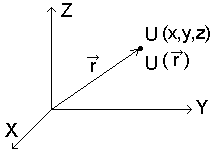 квівалентна поверхня: U=const.

Приклад: поверхня над рівнем моря:

2. В екторне поле –задана векторна величина в кожній точці.

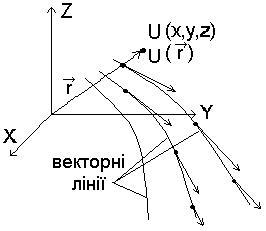
Чим більше вектор, тим густіше проходять векторні лінії.

Векторна величина має модуль і напрямок. Поле характеризується такими величинами: градієнт, дивергенція, ротор, потік.

Ротор характеризує роботу.

- щільність (густина) об’ємного заряду.

Дивергенція – це величина, яка показує де починаються або закінчуються векторні лінії (тобто де існує заряд) там div0, в інших місцях вона дорівнює нулю.

Н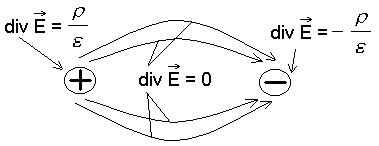 а малюнку показане електростатичне поле ( не вихрове).

Поля поділяються на потенціальні та соленоїдальні.