7.. Дианмич-я модель дпт нв и его структурная схема

Для получения уравнений динамической механической ха­рактеристики двигателя постоянного тока можно непосред­ственно воспользоваться преобразованными уравнениями обоб­щенной машины в осях , :

(3.1)

В соответствии с рис. 3.1,6 в (3.1) можно принять

Показанные на рис. 3.1,б обмотки машины, расположенные на статоре по оси , непосредственно в процессе электро­механического преобразования энергии не участвуют. Обмотка ДП обтекается током якоря и обеспечивает вблизи оси щеток , т. е. в зоне, где осуществляется коммутация тока в про­водниках обмотки якоря, магнитное поле такого направления и значения, при котором процессы коммутации протекают наиболее благоприятно. Компенсационная обмотка КО явля­ется распределенной обмоткой, закладываемой в пазы на главных полюсах аналогично якорной обмотке. Вследствие про­текания по ней тока якорной цепи она создает МДС, ком­пенсирующую МДС реакции якоря по поперечной оси . В машинах без компенсационной обмотки эта реакция якоря искажает форму поля под главными полюсами и в связи с насыщением магнитопровода создает размагничивающую продольную составляющую. Благодаря действию КО влияние поперечной реакции якоря на поле главных полюсов суще­ственно уменьшается. С учетом сказанного можно выразить потокосцепления обмоток через токи:

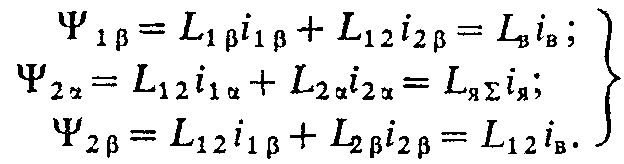(3.2)

Здесь Lв — полная индуктивность обмотки возбуждения, а L_я — суммарная индуктивность рассеяния обмоток ЯО, ДП и КО, так как основная МДС обмотки ЯО по оси  компенсируется МДС компенсационной обмотки. Соответственно со­противление R_я включает в себя все сопротивления обмоток якорной цепи двигателя. С учетом введенных обозначении и (3.2) система уравнений (3.1) запишется в виде

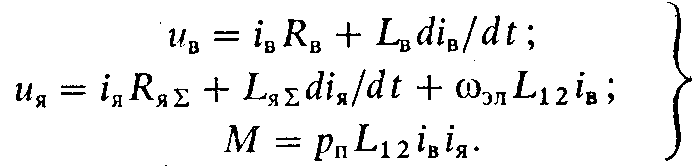(3.3)

Нетрудно видеть, что первые два уравнения полученной системы представляют собой уравнения Кирхгофа для цепей возбуждения и якоря машины, причем последний член урав­нения для цепи якоря есть ЭДС двигателя:

(3.4)

где k = p_nN/2а - конструктивный коэффициент; N - число активных проводников; а — число параллельных ветвей якор­ной обмотки. Момент в (3.3) с учетом (3.4) определяется соотношением

(3.5)

Следовательно, для записи уравнений механической харак­теристики двигателя постоянного тока можно, как это принято, непосредственно использовать схему его цепей на постоян­ном токе, приведенную на рис. 3.2. На этой схеме и в дальней­шем изложении вспомогательные обмотки ДП и КО не пока­зываются, а их сопротивления и индуктивности рассеяния учитываются в R_я и L_я. Получение уравнений (3.3) из урав­нений обобщенной машины, выполненное здесь, имеет целью показать универсальные возможности методики описания дина­мических процессов преобразования энергии. С учетом (3.4) и (3.5) систему (3.3) можно представить в виде

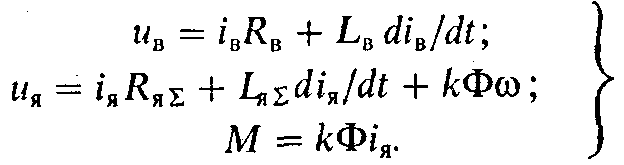(3.6)

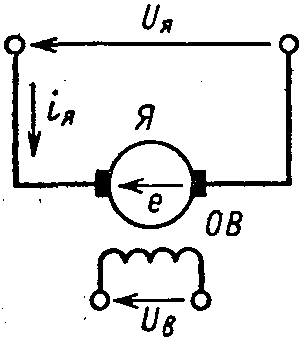
Рис. 3.2. Естественная схема включения двигате­ля с независимым возбуждением

Математическое описание механической характеристики двигателя постоянного то­ка (3.6) при переменном потоке нелинейно в связи с тем, что ЭДС двигателя е и электромагнитный момент М пропорциональны произведениям потока соответственно на скорость и ток якоря. Во многих случаях двигатель с независимым возбуждением работает при постоянном потоке Ф = const, при этом уравнения механи­ческой характеристики линеаризуются и после преобразова­ний математическое описание динамических процессов преоб­разования энергии в двигателе с независимым возбуждением представляется в виде следующего уравнения механической характеристики:

(3.7)

Подстановка М=kФi_я в (3.7) дает уравнение электромеха­нической характеристики:

(3.8)

Как частный результат полученного математического опи­сания могут быть определены уравнения статических электро­механической и механической характеристик двигателя. При постоянном потоке уравнения этих характеристик с помощью (3.7) и (3.8) при dM/dt = di_я/dt = 0 записываются в виде

(3.9)

(3.10)

Рассматривая полученные уравнения, можно заключить, что при Ф = const электромеханическая и механическая харак­теристики двигателя с независимым возбуждением линейны. Поэтому положение каждой характеристики может быть оха­рактеризовано двумя точками: точкой идеального холостого хода, в которой I_я=0; М = 0, и точкой короткого замыкания, в которой  = 0. В соответствии с (3.9) и (3.10) первой из них соответствует скорость идеального холостого хода:

(3.11)

Второй соответствуют момент М_кз и ток I_кз короткого за­мыкания. Их можно определить, решив (3.9) и (3.10) относи­тельно тока и момента:

(3.12)

(3.13)

Положим в этих уравнениях  = 0, получим

(3.14)

Важным показателем электромеханических свойств двига­теля является модуль статической жесткости механической ха­рактеристики _ст. Зависимость _ст от параметров двигателя получим, продифференцировав в соответствии с (2.48) уравне­ние (3.13) по скорости:

(3.15)

Следовательно, модуль статической жесткости определяется соотношением

(3.16)

С помощью (3.11) и (3.16) уравнение статической механи­ческой характеристики двигателя с независимым возбуждением может быть записано в следующих формах:

(3.17)

(3.18)

(3.19)

где

Уравнение электромеханической характеристики с учетом (3.11) и (3.14) может иметь следующие формы записи:

(3.20)

(3.21)