Лекция 8. Геометрические и механические приложения определенного интеграла. Вычисление площадей плоских фигур в прямоугольных и полярных координатах. Вычисление объемов тел по известным площадям параллельных сечений. Вычисление поверхностей и объемов тел вращения. Вычисление длин дуг плоских и пространственных кривых. Вычисление работы переменной силы.

Пискунов Н.С. Дифференциальное и интегральное исчисление.М.,2000.Гл.12, && 1-8.

Бугров Я.С., Никольский С.М.Высшая математика, Т.2 Дифференциальное и интегральное исчисление. М., Дрофа, 2003Гл.7, && 1-3, 5.

И.П. Натансон. Краткий курс высшей математики.,М.,Лань.2005.Гл.6

Геометрические приложения определенного интеграла

Цель сегодняшней лекции состоит не в том, чтобы привести несколько формул для решения конкретных задач, а в том, что бы научить вас использовать данный математический аппарат в решении конкретных задач. Поэтому я буду иногда пренебрегать абсолютной строгостью математического изложения, обращая больше внимания на то, каким образом в решении конкретных задач возникает определенный интеграл.

Геометрические приложения определенного интеграла

Площадь криволинейной трапеции.

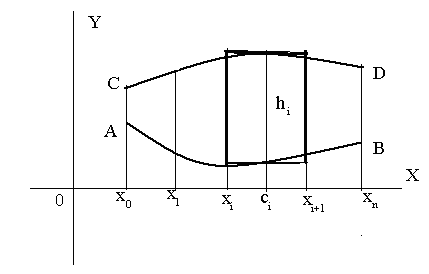
Криволинейной трапецией назовем область, ограниченную линиями: , - кривая АВ, - кривая CD. При этом предполагаем, что при .

Разобьем отрезок на частей точками ( ). Обозначим , где - длина отрезка .

Площадь части криволинейной трапеции, ограниченной линиями обозначим . Тогда полная площадь всей криволинейной трапеции S равна .

Оценим значение величины . Для этого на отрезке выберем произвольную точку . Вычислим значения функций и в этой точке - . Обозначим . Интуитивно понятно, что величина при малом значении будет не очень сильно отличаться от площади криволинейной трапеции, ограниченной линиями , то есть .

Тогда сумма таких площадей по всем отрезкам разбиения

будет близка к площади S криволинейной трапеции, ограниченной линиями:

, то есть .

Понятно, что чем мельче будут отрезки разбиения, тем меньше будет погрешность. Теперь попытаемся перейти немного к более строгим рассуждениям. Полученная сумма является интегральной суммой для функции на отрезке . Следовательно, предел этой суммы при неограниченном уменьшении длин отрезков разбиения равен определенному интегралу от данной функции по отрезку . Таким образом .

Замечание. Если добиваться полной строгости, то мы сначала должны решить вопрос, а что мы будем называть площадью криволинейной трапеции. Что такое площадь прямоугольника – это понятно, а вот что такое площадь произвольной фигуры, мы еще должны определить. При этом наше определение должно быть таким, что бы оно совпадало, по возможности, с нашим интуитивным понятием о площади. В некотором смысле площадью криволинейной трапеции мы и называем предел суммы , и уже потом показываем, что этот предел равен определенному интегралу.

Пример. Найти площадь фигуры, ограниченной линиями , , .

Очевидно, что при имеем . Тогда

.

Пример. Найти площадь фигуры, ограниченной линиями:

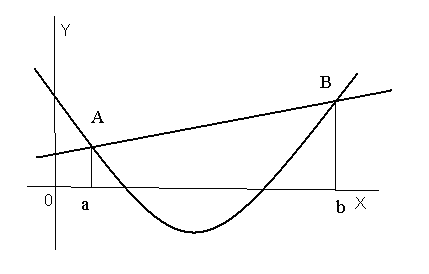
В этом примере значения не указаны. Попробуем нарисовать кривые. Сначала сделаем грубый рисунок. Первая кривая – это парабола, ветви которой направлены вверх, а вторая – это прямая с положительным угловым коэффициентом. Для того чтобы найти значения , мы должны определить точки пересечения кривых. Для этого решаем систему уравнений

Получаем .

То есть .

Теперь более точно нарисуем графики функций, хотя для решения задачи вычисления площади в этом уже необходимости нет.

Следовательно

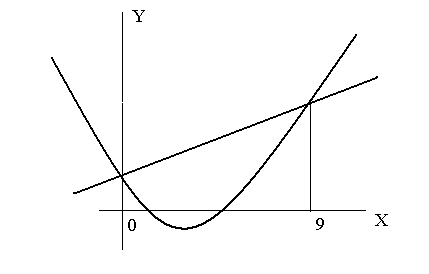
Пример. Найти площадь фигуры, ограниченной линиями:

Решение. Найдем точки пересечения кривых. Для этого решаем систему уравнений.

.

Получаем: .

Схематично фигура изображена на рисунке.

Следовательно

= .

Теперь рассмотрим пример вычисления площади криволинейной трапеции, ограниченной линиями , в случае, когда кривая задана не в явном виде, а параметрически , где , . При этом предполагаем, что функции непрерывны на отрезке , а функция монотонна и имеет непрерывную производную на этом отрезке.

Тогда для вычисления площади имеем соотношение

.

В полученном определенном интеграле сделаем замену переменных

. Тогда , . Пределы интегрирования заменяются соответственно: на ; на .

Получаем .

Пример. Найти площадь фигуры, ограниченной линиями

Поскольку x и y неотрицательны, то параметр изменяется на отрезке .

Схематично фигура изображена на рисунке.

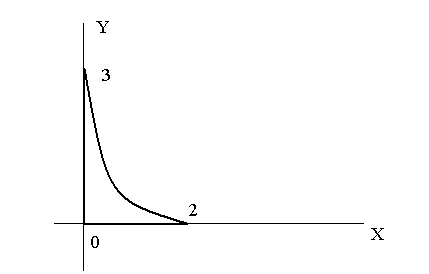
Выражение для площади имеет вид .

Делая замену переменных , получаем , . Из условия : получаем ; при получаем .

Тогда

Воспользуемся формулами косинуса двойного угла

= =

+ = =

= .

Пример. Найти площадь эллипса .

Эллипс с полуосями - фигура, симметричная относительно всех координатных осей, поэтому достаточно найти площадь в первой координатной четверти.

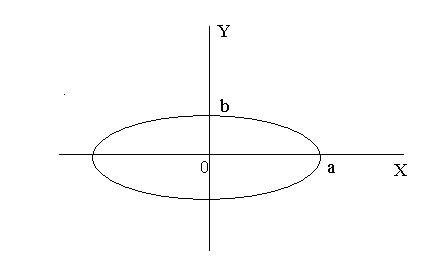
В первой четверти зададим эллипс параметрически

Тогда значению соответствует , значению соответствует . Следовательно

= .

Рассмотрим задачу о вычислении площади криволинейного сектора.

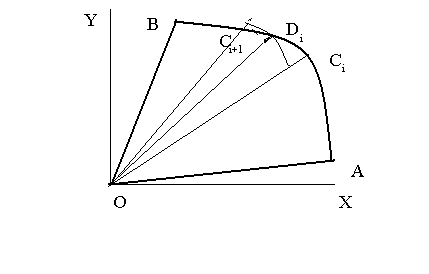
Криволинейным сектором называется область, ограниченная линиями, уравнения которых в полярной системе координат ( ) имеют вид: 1)два луча ; 2)линия .

На рисунке (предполагается, что ось X совпадает с полярной осью) лучу соответствует ОА (угол AOX равен α), лучу соответствует ОВ (угол ВOX равен β), линии соответствует кривая АВ.

Разделим область на части лучами , ,…, (луч ), (луч ),…, . Обозначим . Площадь криволинейного сектора обозначим .

Тогда полная площадь S криволинейного сектора ВОА может быть представлена в виде .

Оценим значение , предполагая, что - достаточно малая величина. Выберем значение угла , где (луч ). Заменим криволинейный сектор круговым сектором радиуса , где . При малом значении есть все основания полагать, что их площади отличаются незначительно. Соответствующая площадь кругового сектора радиуса равна . Тогда имеем .

Полученная сумма является интегральной суммой для функции на отрезке . Переходя к пределу, при стремлении максимального значения к нулю, получаем

.

Замечание.

Пусть область ограничена линиями, уравнения которых в полярной системе координат ( ) имеют вид:

1)два луча ;

2)линии , где при .

Тогда ее площадь вычисляется по формуле

Пример. Найти площадь фигуры, ограниченной линией:

Данная фигура схематично изображена на рисунке

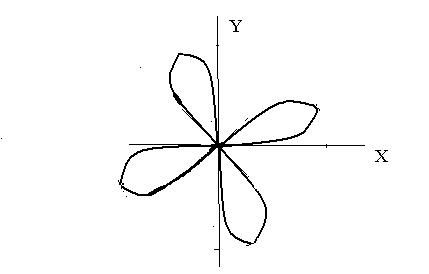
Данный «цветок» состоит из четырех совершенно одинаковых «лепестков». (Напомним, что по смыслу полярной системы координат значение , поэтому для тех значений угла , при которых , точек на линии не существует). Поэтому достаточно найти площадь одного лепестка и умножить ее на четыре. «Первый лепесток» ограничен лучами и кривой . Следовательно

.

Пример. Найти площадь фигуры, ограниченной линиями:

Данная фигура схематично изображена на рисунке.

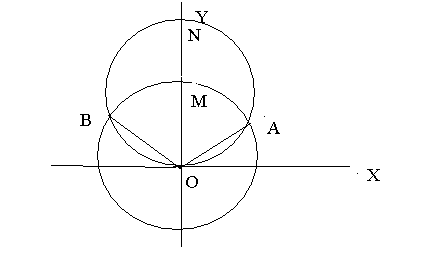
Она ограничена кривыми BNA и BMA . Найдем точки пересечения кривых . Получаем . На отрезке уравнение имеет два корня , . Следовательно, в полярной системе координат луч ОА имеет уравнение , луч ОВ - , кривая BNA - , кривая BMA - .

Тогда =

= .

Вычисление объема тела по известным площадям параллельных сечений.

Пусть имеется некоторое тело в пространстве. Обозначим - площади его сечений плоскостями, перпендикулярными оси Z. Требуется определить объем тела.

Будем предполагать, что плоскости пересекают данное тело при значениях z, лежащих на отрезке [a;b]. Разобьем отрезок [a;b] на n частей точками ( =a), , …, , ,…, ( =b). Обозначим: , - объем слоя толщины , заключенного между сечениями z= и z= . Если достаточно мало, то приближенно этот объем можно оценить как объем цилиндра высоты и площади основания , где , то есть .

Тогда полный объем V приближенно равен

.

Полученная сумма является интегральной суммой для функции Q(z) на отрезке [a;b]. Окончательная формула для объема имеет вид

Замечание. В частности, если тело получено вращением относительно оси X криволинейной трапеции, ограниченной линиями: , , , где при , то площадь сечения равна Q(x)= и объем соответственно равен .

.

Пример. Найти объем эллипсоида .

Рассмотрим сечения данного эллипсоида плоскостями, перпендикулярными оси Z. Преобразуем уравнение эллипсоида

.

Следовательно, сечением эллипсоида является эллипс с полуосями , . Как было показано ранее, площадь эллипса с полуосями равна . Следовательно, площадь сечения эллипсоида Q(z) выражается формулой , где .

Тогда .

Пример. Найти объем тела, полученного вращением вокруг оси ОХ криволинейной трапеции, ограниченной линиями.

Решение. .

Вычисление длин кривых.

Предположим, что в пространстве (X,Y,Z) параметрически задана кривая . Требуется определить длину дуги данной кривой, если

значения параметра t при этом изменяются на отрезке [a;b]

(дуга АВ на рисунке).

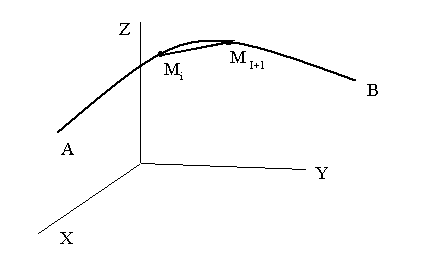
Относительно функций будем предполагать, что они являются непрерывными и имеют непрерывные производные на отрезке [a;b].

Разобьем отрезок [a;b] на n частей точками ( =a), , …, , ,…, ( =b). Обозначим: , - длина дуги , где координаты точек соответственно равны , . Если достаточно мало, то приближенно - длину дуги можно заменить величиной - длиной секущей . Рассмотрим вектор = , где , , .

Значение равно модулю вектора , то есть

.

Согласно теореме Лагранжа

, , , где точки лежат на отрезке .

Тогда L - длина дуги АВ приближенно равна

.

Полученная сумма не является интегральной суммой, поскольку точки не обязаны совпадать. Однако, поскольку лежат на отрезке длиной , то можно показать, что ее предел при стремлении к нулю максимального значения равен пределу интегральной суммы для функции на отрезке [a;b] .

Следовательно .

С точки зрения математики вопрос о длине кривой, это не совсем простой вопрос. Фактически мы определяем длину кривой, как предел длин секущих и показываем, что этот предел равен полученному определенному интегралу.

Замечание 1. Если кривая задана параметрически на плоскости , где , то ее длина вычисляется по аналогичной формуле

.

Замечание 2. Если кривая на плоскости задана уравнением , где , то можно считать, что роль параметра играет независимая переменная . Тогда длина кривой вычисляется по формуле .

Пример. Найти длину кривой, заданной уравнением:

Решение. =

= .

Пример. Найти длину кривой, заданной уравнениями:

Решение. =

= .

Пример. Найти длину кривой, заданной уравнениями:

Решение. =

= .

Замечание. Если кривая задана уравнением в полярной системе координат , где , то, поскольку , ее можно рассматривать как заданную параметрически ,

где роль параметра играет угол φ ( ). Тогда длина кривой вычисляется по формуле

.

Поскольку , , то

Пример. Найти длину кривой, заданной уравнением , где .

Решение.

.