15.7. Трансформатор с ферромагнитным сердечником

Э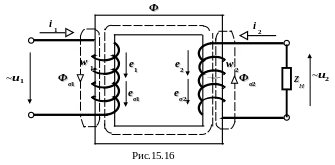 лектромагнитные явления в трансформаторе со стальным сердечником по­добны явлениям в воздушном трансформаторе, но магнитный поток, который пронизывает обе обмотки, замыкается не по воздуху, а через стальной сердечник (рис.15.16).

При нагрузке трансформатора существуют три магнитных потока: Ф – ос­новной в сердечнике, Ф_σ1 – рассеяния, связанный только с первичной обмоткой, Ф_σ2 – рассеяния, связанный только со вторичной обмоткой.

Основной магнитный поток наводит в первичной и вторичной обмотках э.д.с. соответственно е₁ и е₂. Магнитные потоки рассеяние Ф_σ1 и Ф_σ2 наводят в первич­ной и вторичной обмотках э.д.с. соответственно е_σ1 и е_σ1.

Напряжение u₁, приложенное к первичной обмотке, уравновешивается паде­нием напряжения на активном сопротивлении обмотки и электродвижущими си­лами е_σ1 и е_σ1, т.е.

,

(15.17)

где L_σ1 – индуктивность, обусловленная магнитным потоком рассеяния Ф_σ1, Гн.

Знайдемо діюче значення е.р.с. самоіндукції:

;

,

де

.

Тоді

.

(15.16)

15.7. Трансформатор з феромагнітним осердям

Електромагнітні явища в трансформаторі зі сталевим осердям подібні явищам у повітряному трансформаторі, але магнітний потік, який пронизує обидві обмотки, замикається не по повітрю, а через сталеве осердя (рис.15.16).

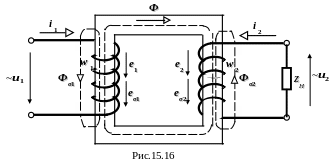
При навантаженні трансформатора існують три магнітних потоки: Ф – основний у осерді, Ф_σ1 – розсіювання, зв'язаний тільки з первинною обмоткою, Ф_σ2 – розсіювання, зв'язаний тільки з вторинною обмоткою.

Основний магнітний потік наводить у первинній і вторинній обмотках е.р.с. відповідно е₁ і е₂. Магнітні потоки розсіювання Ф_σ1 і Ф_σ2 наводять у первинній і вторинній обмотках е.р.с. відповідно е_σ1 і е_σ1.

Напруга u₁, прикладена до первинної обмотки, врівноважується спаданням напруги на активному опорі обмотки та електрорушійними силами е_σ1 і е_σ1, тобто

,

(15.17)

де L_σ1 – індуктивність, обумовлена магнітним потоком розсіювання Ф_σ1, Гн.

Во вторичной обмотке э.д.с., которые наводятся магнитными потоками Ф и Ф_σ2, уравновешивается падениями напряжений на активном сопротивлении об­мотки и сопротивлении нагрузки, т.е.

или

,

(15.18)

где L_σ2 – индуктивность, обусловленная магнитным потоком рассеяния Ф_σ2, Гн.

Заменим реальный трансформатор эквивалентным (рис.15.17).

Трансформатор с зажимами 1–2 и 1′–2′ называется идеальным трансформа­тором.

Коэффициент трансформации трансформатора

.

(15.19)

Рассмотрим сначала идеальный трансформатор, в котором r₁ = 0; x_σ1 = 0; r₂ = 0; x_σ2 = 0; w₁ = w₂.

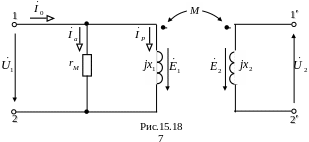
При холостом ходе такой трансформатор не отличается от обычной идеальной катушки и может быть изображён схемой замещения (рис.15.18).

r_м

1

2

М

1’

2’

Рис.15.187

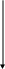
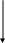
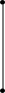
У вторинній обмотці е.р.с., яка наводяться магнітними потоками Ф і Ф_σ2, врівноважується спаданням напруг на активному опорі обмотки та опорі навантаження, тобто

або

,

(15.18)

де L_σ2 – індуктивність, обумовлена магнітним потоком розсіювання Ф_σ2, Гн.

Замінимо реальний трансформатор еквівалентним (рис.15.17).

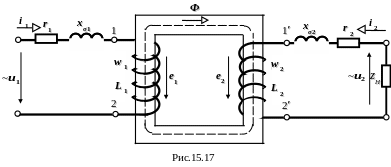
Трансформатор із затисками 1–2 і 1′–2′ називається ідеальним трансформатором.

Коефіцієнт трансформації трансформатора

.

(15.19)

Розглянемо спочатку ідеальний трансформатор, у якому r₁ = 0; x_σ1 = 0; r₂ = 0; x_σ2 = 0; w₁ = w₂.

При холостому ході такий трансформатор не відрізняється від звичайної ідеальної котушки і може бути зображений схемою заміщення (рис.15.18).

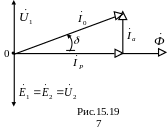
Построим векторную диаграмму идеального трансформатора при холостом ходе (рис.15.19).

Намагничивающая сила при холостом ходе

,

(15.20)

где Z_м – комплекс магнитного сопротивления сердечника, 1/Гн;

– комплекс основ­ного магнитного потока, Вб.

Уравнение для первичного контура:

.

(15.21)

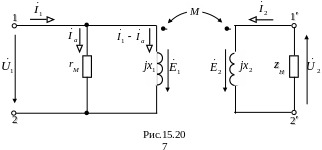
Составим теперь схему замещения идеального трансформатора при его на­грузке (рис.15.20).

Если к зажимам вторичной обмотки подключить нагрузку с сопротивлением Z_н, то в ней будет проходить ток , который, в свою очередь, будет стремиться уменьшить магнитный поток , а это приведёт к уменьшению э.д.с. , вследст­вие чего ток возрастёт до такой величины, при которой магнитный поток при­обретёт первоначальное значение и будет выполняться уравнение (15.21). Та­ким образом, появление тока во вторичном контуре приводит к увеличению тока в первичном контуре.

Побудуємо векторну діаграму ідеального трансформатора при холостому ході (рис.15.19).

Намагнічующа сила при холостому ході

,

(15.20)

де Z_м – комплекс магнітного опору осердя, 1/Гн;

– комплекс основного магнітного потоку, Вб.

Рівняння для первинного контуру:

.

(15.21)

Складемо тепер схему заміщення ідеального трансформатора при його навантаженні (рис.15.20).

Якщо до затисків вторинної обмотки підключити навантаження з опором Z_н, то в ній буде проходити струм , який, у свою чергу, буде намагатися зменшити магнітний потік , а це приведе до е.р.с. , внаслідок чого струм зросте до такої величини, при якій магнітний потік набуде початкового значення і буде виконуватися рівняння (15.21). Таким чином, поява струму у вторинному контурі приводить до збільшення струму в первинному контурі.

В нагруженном трансформаторе магнитный поток в сердечнике равен маг­нитному потоку при холостом ходе, т.е. всегда Ф = const.

При нагрузке магнитный поток создаётся под действием намагничиваю­щих сил первичной и вторичной обмоток:

.

(15.22)

Сравнив (15.20) и (15.22), находим:

.

(15.23)

При равенстве количества витков первичной и вторичной обмоток

,

(15.24)

откуда

.

(15.25)

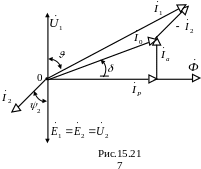
Построим векторную диаграмму идеального трансформатора при нагрузке (рис.15.21).

Преобразуем схему замещения идеального трансформатора, для чего изба­вимся от индуктивной связи. Если соединить одноимённые зажимы обмоток трансформатора между собой, то режим работы трансформатора не изменится.

Рассмотрим сначала индуктивно связанные элементы, которые теперь имеют общую точку. Коэффициент связи двух элементов в данном случае равен единице, поскольку весь магнитный поток полностью сцеплен с витками первичной и вто­ричной обмоток, т.е.

,

(15.26)

У навантаженому трансформаторі магнітний потік у осерді дорівнює магнітному потоку при холостому ході, тобто завжди Ф = const.

При навантаженні магнітний потік створюється під дією намагнічующих сил первинної і вторинної обмоток:

.

(15.22)

Порівнявши (15.20) і (15.22), знаходимо:

.

(15.23)

При рівності кількості витків первинної і вторинної обмоток

,

(15.24)

звідки

.

(15.25)

Побудуємо векторну діаграму ідеального трансформатора при навантаженні (рис.15.21).

Перетворимо схему заміщення ідеального трансформатора, для чого розв'яжемо індуктивний зв'язку. Якщо з'єднати однойменні затиски обмоток трансформатора між собою, то режим роботи трансформатора не зміниться.

Розглянемо спочатку індуктивно зв'язані елементи, які тепер мають загальну точку. Коефіцієнт зв'язку двох елементів у даному випадку дорівнює одиниці, оскільки весь магнітний потік повністю зчеплений з витками первинної і вторинної обмоток, тобто

,

(15.26)

поэтому, учитывая, что w₁ = w₂, находим:

.

(15.27)

Заменим теперь часть схемы с индуктивно связанными элементами с общей точкой (рис.15.22а) на эквивалентную схему без индуктивной связи (рис.15.22б).

Теперь

;

;

.

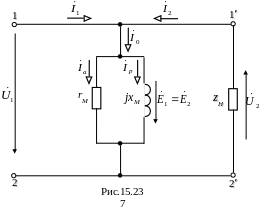
С учётом найденного схема принимает вид, показанный на рис.15.22в, а схема замещения идеального трансформатора – вид, изображённый на рис.15.23.

тому, з огляду на те, що w₁ = w₂, знаходимо:

.

(15.27)

Замінимо тепер частину схеми з індуктивно зв'язаними елементами з загальною точкою (рис.15.22а) на еквівалентну схему без індуктивного зв'язку (рис.15.22б).

Тепер

;

;

.

З урахуванням знайденого схема приймає вигляд, показаний на рис.15.22в, а схема заміщення ідеального трансформатора – вигляд, зображений на рис.15.23.

Если теперь учесть активные и индуктивные сопротивления рассеяния обеих обмоток, то для трансформатора, у которого w₁ = w₂, получим схему замещения, приведенную на рис.15.24.

Запишем уравнения первичного и вторичного контуров цепи:

;	(15.28)
.	(15.29)

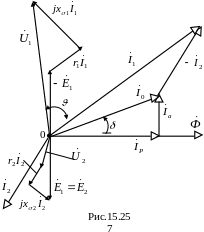
Построим векторную диаграмму цепи (рис.15.25).

Якщо тепер врахувати активні й індуктивні опори розсіювання обох обмоток, то для трансформатора, у якого w₁ = w₂, одержимо схему заміщення, приведену на рис.15.24.

Запишемо рівняння первинного і вторинного контурів кола:

;	(15.28)
.	(15.29)

Побудуємо векторну діаграму кола (рис.15.25).