Тема 14

Нелинейные цепи переменного тока

15.1. Общие положения

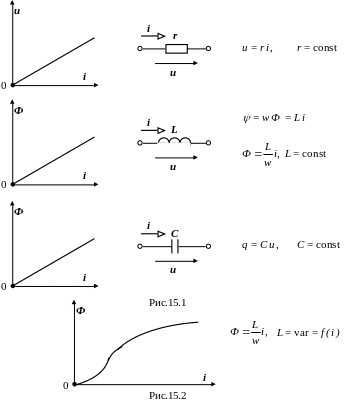
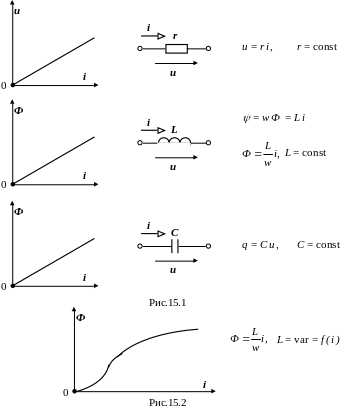
Для линейных цепей переменного тока зависимости между напряжением и током в активном сопротивлении u(i), между магнитным потоком и током в ин­дуктивности Ф(i), между зарядом и напряжением в ёмкости q(u) имеют линейный ха­рактер (рис.15.1), а для нелинейных цепей – нелинейный характер, например, на рис.15.2.

Тема 15

НЕЛІНІЙНІ кола зМІННОГО струму

15.1. Загальні положення

Для лінійних кіл змінного струму залежності між напругою і струмом в активному опорі u(i), між магнітним потоком і струмом в індуктивності Ф(i), між зарядом і напругою в ємності q(u) мають лінійний характер (рис.15.1), а для нелінійних кіл – нелінійний характер, наприклад, на рис.15.2.

15.2. Нелинейная индуктивность

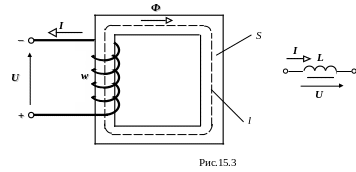
Рассмотрим катушку с ферромагнитным сердечником, включённую в цепь постоянного тока. При этом будем считать, что магнитный поток, который замыкается час­тично по воздуху (поток рассеяния), равен нулю (рис.15.3).

Запишем основные соотношения, полученные ранее:

;	;	;
.			(15.1)

Найдём зависимость Ф(I). Известно, что , . Поскольку S, w, l – величины постоянные, то зависимость Ф(I) аналогична зависимости В(Н), т.е. повторяет кривую намагничивания (рис.15.4).

15.2. Нелінійна індуктивність

Розглянемо котушку з феромагнітним осердям, включену в коло постійного струму. При цьому будемо вважати, що магнітний потік, який замикається частково по повітрю (потік розсіювання), дорівнює нулю (рис.15.3).

Запишемо основні співвідношення, одержані раніше:

;	;	;
.			(15.1)

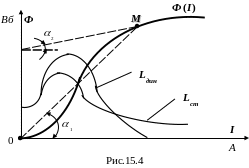
Знайдемо залежність Ф(I). Відомо, що , . Оскільки S, w, l – величини постійні, то залежність Ф(I) аналогічна залежності В(Н), тобто повторює криву намагнічування (рис.15.4).

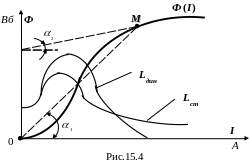
Индуктивность катушки, как видно из формулы, зависит только от перемен­ной части . Если ток увеличивать, то увеличится напряжённость магнит­ного поля , а соответственно и магнитная индукция В. Но магнитная индук­ция на нелинейной части характеристики увеличивается не пропорцио­нально напряжённости. Так, в области, близкой к насыщению, магнитная индук­ция увеличивается меньше по сравнению с увеличением напряжённости, т.е. маг­нитная проницаемость уменьшается, а это значит, что уменьшается и индук­тивность L.

Каждой точке характеристики Ф(I) соответствует определённое значение статической индуктивности

(15.2)

и динамической индуктивности

,

(15.3)

где m_L – масштаб индуктивности, Гн/мм.

15.3. Идеальная катушка с ферромагнитным сердечником в цепи переменного тока

Подключим идеальную катушку с ферромагнитным сердечником к источнику пе­ременного синусоидального тока. При этом будем считать, что идеальная катушка с ферромагнитным сердечником не имеет петли гистерезиса, активное сопротив­ление её равно нулю, магнитный поток рассеяния отсутствует (рис.15.5).

Індуктивність котушки, як видно з формули, залежить тільки від змінної частини . Якщо струм збільшувати, то збільшиться напруженість магнітного поля , а відповідно і магнітна індукція В. Але магнітна індукція на нелінійній частині характеристики збільшується не пропорційно напруженості. Так, в області, близької до насичення, магнітна індукція збільшується менше в порівнянні зі збільшенням напруженості, тобто магнітна проникність зменшується, а це значить, що зменшується й індуктивність L.

Кожній точці характеристики Ф(I) відповідає певне значення статичної індуктивності

(15.2)

і динамічної індуктивності

,

(15.3)

де m – масштаб індуктивності, Гн/мм.

15.3. Ідеальна котушка з феромагнітним осердям у колі змінного струму

Підключимо ідеальну котушку з феромагнітним осердям до джерела змінного синусоїдного струму. При цьому будемо вважати, що ідеальна котушка з феромагнітним осердям не має петлі гістерезиса, активний опір її дорівнює нулю, магнітний потік розсіювання відсутній (рис.15.5).

Запишем основные соотношения для этого случая:

;	;	;
.			(15.4)

Зависимость Ф(i) для катушки с ферромагнитным сердечником такая же, как и Ф(I) (см. рис.15.4).

Рассмотрим форму кривой тока в цепи с нелинейной индуктивностью при синусоидальном напряжении источника. Предположим, что напряжение источ­ника

.

(15.5)

Пренебрегая активным сопротивлением катушки с ферромагнитным сердеч­ником и магнитным потоком рассеяния, можем записать:

u = – e;

;

,

откуда

;
.	(15.6)

Таким образом, при синусоидальном напряжении магнитный поток также синусоидальный.

Д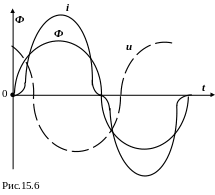 ля нахождения кривой тока в катушке с ферромагнитным сердечником, воспользуемся зависимостями Ф(t) и Ф(i) и построим зависимость i(t) графиче­ским способом (рис.15.6).

Запишемо основні співвідношення для цього випадку:

;	;	;
.			(15.4)

Залежність Ф(i) для котушки з феромагнітним осердям така ж, як і Ф(I) (див. рис.15.4).

Розглянемо форму кривої струму в колі з нелінійною індуктивністю при синусоїдній напрузі джерела. Припустимо, що напруга джерела

.

(15.5)

Зневажаючи активним опором котушки з феромагнітним осердям і магнітним потоком розсіювання, можемо записати:

u = – e;

;

,

звідки

;
.	(15.6)

Таким чином, при синусоїдній напрузі магнітний потік також синусоїдний.

Д ля знаходження кривої струму в котушці з феромагнітним осердям, скористаємося залежностями Ф(t) і Ф(i) та побудуємо залежність i(t) графічним способом (рис.15.6).

Итак, кривая тока несинусоидальна. Заменим её эквивалентной синусоидой:

;
;	,

где I – действующее значение несинусоидального тока, А;

;

.

П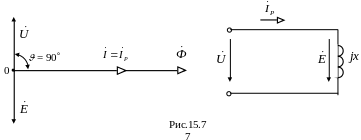 остроим векторную диаграмму идеальной катушки с ферромагнитным сер­дечником и составим её схему замещения (рис.15.7).

Запишем уравнение для катушки:

.

(15.7)

где I_p – реактивный (намагничивающий) ток, А;

x = wL – индуктивное сопротивле­ние, Ом,

L – эквивалентная индуктивность, Гн.

Потокосцепление катушки

.

(15.8)

Р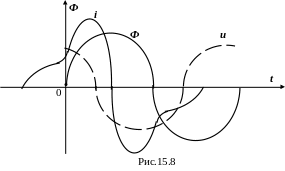 ассмотрим теперь катушку с ферромагнитным сердечником с учётом петли гистерезиса. Если построить кривую тока в этом случае на базе зависимостей Ф(t) и Ф(i), которая имеет форму петли гистерезиса, то получим несинусоидальную форму кривой тока, рис.15.8.

Отже, крива струму несинусоїдна. Замінимо її еквівалентною синусоїдою:

;
;	,

де I – діюче значення несинусоїдного струму, А;

;

.

П обудуємо векторну діаграму ідеальної котушки з феромагнітним осердям та складемо її схему заміщення (рис.15.7).

Запишемо рівняння для котушки:

.

(15.7)

де I_p – реактивний (намагнічующий) струм, А;

x = w – індуктивний опір, Ом,

L – еквівалентна індуктивність, Гн.

Потокозчеплення котушки

.

(15.8)

Р озглянемо тепер котушку з феромагнітним осердям з урахуванням петлі гістерезиса. Якщо побудувати криву струму в цьому випадку на базі залежностей Ф(t) і Ф(i), яка має форму петлі гистерезиса, то одержимо несинусоїдну форму кривої струму, рис.15.8.

Если несинусоидальную кривую тока заменить эквивалентной синусоидой, то можно записать:

;

, где ;

;

.

Построим векторную диаграмму катушки и составим её схему замещения для этого случая (рис.15.9). На схеме I_а – активная составляющая тока, I_p – реактивная составляющая тока.

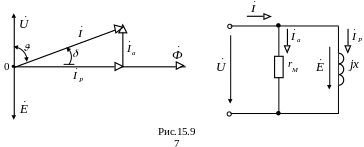
Появление в схеме активного сопротивления r_м (активное сопротивление ка­тушки равно нулю) обусловлено потреблением катушкой с ферромагнитным сер­дечником активной мощности, которая тратится на гистерезис и вихревые токи.