14.9. Расчёт разветвлённых магнитных цепей

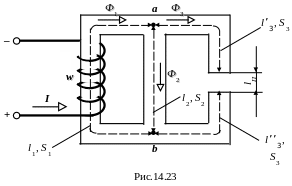
Для заданной магнитной цепи (рис14.23) известны геометрические размеры магнитопровода, кривая намагничивания, магнитный поток Ф₃. Необходимо найти намагничивающую силу F.

Порядок расчёта:

1. Составляем эквивалентную расчётную схему магнитной цепи и выбираем условно положительные направления магнитных потоков (рис.14.24).

2. Будуємо залежність Ф = f (F) (рис.14.22).

3. Відклавши значення заданої намагнічующої сили, за допомогою кривої Ф = f (F) визначаємо відповідне значення магнітного потоку Ф.

14.9. Розрахунок розгалужених магнітних кіл

Для заданого магнітного кола (рис.14.23) відомі геометричні розміри магнітопровіда, крива намагнічування, магнітний потік Ф₃. Необхідно знайти намагнічующу силу F.

Порядок розрахунку:

1. Складаємо еквівалентну розрахункову схему магнітного кола і вибираємо умовно позитивні напрями магнітних потоків (рис.14.24).

2. Для нахождения намагничивающей силы запишем уравнения по второму закону Кирхгофа для первого контура:

F = R_м1Ф₁ + R_м2Ф₂ или F = H₁l₁ + U_м.ab.

Таким образом, задача сводится к нахождению H₁ и U_м.ab.

3. Магнитное напряжение на участке ab:

U_м.ab = R_м3Ф₃ + R_мпФ₃

или

U_м.ab = H₃l₃ + H_пl_п ,

где

l₃ = l’₃ + l’’₃.

Зная Ф₃, определяем , а потом с помощью кривой намагничивания находим H₃. Поскольку , то подставив значения, находим U_м.ab.

4. Напряжённость H₁ находим с помощью кривой намагничивания, определив сначала магнитную индукцию . Магнитный поток Ф₁ = Ф₂ + Ф₃. При этом Ф₂ = В₂S₂. Для определения магнитной индукции В₂ сначала находим напряжённость магнитного поля на участке l₂, воспользовавшись законом Ома:

U_м.ab = R_м2Ф₂ = H₂l₂ .

2. Для визначення намагнічующої сили запишемо рівняння за другим законом Кірхгофа для першого контуру:

F = R_м1Ф₁ + R_м2Ф₂ або F = H₁l₁ + U_м.ab.

Таким чином, задача зводиться до визначення H₁ та U_м.ab.

3. Магнітна напруга на ділянці ab:

U_м.ab = R_м3Ф₃ + R_мпФ₃

або

U_м.ab = H₃l₃ + H_пl_п ,

де

l₃ = l’₃ + l’’₃.

Знаючи Ф₃, визначаємо , а потім за допомогою кривої намагнічування знаходимо H₃. Оскільки , то підставивши значення, знаходимо U_м.ab.

4. Напруженість H₁ знаходимо за допомогою кривої намагнічування, визначивши спочатку магнітну індукцію . Магнітний потік Ф₁ = Ф₂ + Ф₃. При цьому Ф₂ = В₂S₂. Для визначення магнітної індукції В₂ спочатку знаходимо напруженість магнітного поля на ділянці l₂, скориставшись законом Ома:

U_м.ab = R_м2Ф₂ = H₂l₂ .

откуда

.

С помощью кривой намагничивания находим магнитную индукцию В₂ и рассчитываем магнитный поток Ф₂. После чего определяем магнитную индукцию В₁ по формуле и напряжённость Н₁ с помощью кривой намагничивания.

5. По найденным значениям рассчитываем намагничивающую силу F.

Пусть теперь заданы все геометрические размеры магнитопровода, кривая намагничивания и намагничивающая сила. Необходимо найти все магнитные потоки в ветвях цепи.

Порядок расчёта:

1. Составляем расчётную схему цепи и выбираем условно положительные направления магнитных потоков.

2. Для узла а записываем уравнение по первому закону Кирхгофа:

Ф₁ – Ф₂ – Ф₃ = 0 .

или

Ф₁ = Ф₂ + Ф₃ .

3. Поскольку цепь нелинейная, задачу решаем графо-аналитическим методом. Для этого сначала строим вспомогательные характеристики:

Ф₁ = f(U_м.ab);

Ф₂ = f’(U_м.ab);

Ф₃ = f’’(U_м.ab).

3.1. Для первой ветви по закону Ома можем записать:

,

откуда

U_м.ab = F – R_м1Ф₁.

или

U_м.ab = F – H₁l₁ .

звідки

.

За допомогою кривої намагнічування знаходимо магнітну індукцію В₂ та розраховуємо магнітний потік Ф₂. Після чого визначаємо магнітну індукцію В₁ за формулою та напруженість Н₁ за допомогою кривої намагнічування.

5. За знайденими значеннями розраховуємо намагнічующу силу F.

Нехай тепер задані всі геометричні розміри магнітопровіда, крива намагнічування і намагнічующа сила. Необхідно знайти всі магнітні потоки в розгалуженнях кола.

Порядок розрахунку:

1. Складаємо розрахункову схему кола і вибираємо умовно позитивні напрями магнітних потоків.

2. Для вузла а записуємо рівняння за першим законом Кірхгофа:

Ф₁ – Ф₂ – Ф₃ = 0 .

або

Ф₁ = Ф₂ + Ф₃ .

3. Оскільки коло нелінійне, задачу вирішуємо графо-аналітичним методом. Для цього спочатку будуємо допоміжні характеристики:

Ф₁ = f(U_м.ab);

Ф₂ = f’(U_м.ab);

Ф₃ = f’’(U_м.ab).

3.1. Для першого розгалуження за законом Ома можемо записати:

,

звідки

U_м.ab = F – R_м1Ф₁.

або

U_м.ab = F – H₁l₁ .

Чтобы построить вспомогательную характеристику Ф₁ = f(U_м.ab), задаёмся рядом значений магнитной индукции В₁, определяем с помощью кривой намагничивания напряжённость магнитного поля Н₁, потом магнитное напряжение U_м.ab и соответствующие значения магнитного потока Ф₁.

3.2. Для второй ветви по закону Ома можем записать:

,

откуда

U_м.ab = R_м2Ф₂.

или

U_м.ab = H₂l₂ .

Чтобы построить вспомогательную характеристику Ф₂ = f’(U_м.ab), задаёмся рядом значений магнитной индукции В₂, определяем с помощью кривой намагничивания напряжённость магнитного поля Н₂, потом магнитное напряжение U_м.ab и соответствующие значения магнитного потока Ф₂.

3.3. Для третьей ветви по закону Ома можем записать:

,

откуда

U_м.ab = R_м3Ф₃ + R_м.пФ₃.

или

U_м.ab = H₁l₁ + H_пl_п .

Чтобы построить вспомогательную характеристику Ф₃ = f’’(U_м.ab), задаёмся рядом значений магнитной индукции В₃, определяем с помощью кривой намагничивания напряжённость магнитного поля Н₃, потом магнитное напряжение U_м.ab и соответствующие значения магнитного потока Ф₃.

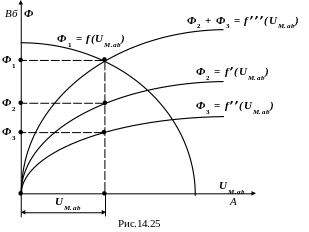
Все полученные зависимости наносим на одну плоскость (рис.4.25).

По первому закону Кирхгофа Ф₁ = Ф₂ + Ф₃. Поэтому строим вспомогательную характеристику Ф₂ + Ф₃ = f’’’(U_м.ab). Точка пересечения а кривых Ф₁ = f(U_м.ab) и Ф₂ + Ф₃ = f’’’(U_м.ab) определяет магнитное напряжение U_м.ab. Потом определяем магнитные потоки Ф₁, Ф₂, Ф₃.

Щоб побудувати допоміжну характеристику Ф₁ = f(U_м.ab), задаємося кількома значеннями магнітної індукції В₁, визначаємо за допомогою кривої намагнічування напруженість магнітного поля Н₁, потім магнітну напругу U_м.ab та відповідні значення магнітного потоку Ф₁.

3.2. Для другого розгалуження за законом Ома можемо записати:

,

звідки

U_м.ab = R_м2Ф₂.

або

U_м.ab = H₂l₂ .

Щоб побудувати допоміжну характеристику Ф₂ = f’(U_м.ab), задаємося кількома значеннями магнітної індукції В₂, визначаємо за допомогою кривої намагнічування напруженість магнітного поля Н₂, потім магнітну напругу U_м.ab та відповідні значення магнітного потоку Ф₂.

3.3. Для третього розгалуження за законом Ома можемо записати:

,

звідки

U_м.ab = R_м3Ф₃ + R_м.пФ₃.

або

U_м.ab = H₁l₁ + H_пl_п .

Щоб побудувати допоміжну характеристику Ф₃ = f’’(U_м.ab), задаємося кількома значеннями магнітної індукції В₃, визначаємо за допомогою кривої намагнічування напруженість магнітного поля Н₃, потім магнітну напругу U_м.ab та відповідні значення магнітного потоку Ф₃.

Всі отримані залежності наносимо на одну площину (рис.4.25).

За першим законом Кірхгофа Ф₁ = Ф₂ + Ф₃. Тому будуємо допоміжну характеристику Ф₂ + Ф₃ = f’’’(U_м.ab). Точка перетинання а кривих Ф₁ = f(U_м.ab) та Ф₂ + Ф₃ = f’’’(U_м.ab) визначає магнітну напругу U_м.ab. Потім визначаємо магнітні потоки Ф₁, Ф₂, Ф₃.