22.Нормированное уравнение плоскости.

Г де:

-углы, образуемые нормальным вектором плоскости с осями координат; p- расстояние от начала координат до плоскости.

Приведение общего уравнения плоскости к нормальному виду:

З десь

нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если произвольно, если D = 0 .

23.Прямая в пространстве. Общее уравнение прямой

П рямая в пространстве может быть задана также как пересечение двух плоскостей, если плоскости не параллельны:

Все формы задания прямой в пространстве взаимосвязаны.

24.Параметрическое и Каноническое уравнение прямой.

Параметрическое:

Векторное уравнение (13.2) в координатной форме представляется следующим образом

Каноническое:

Исключив t из уравнения (13.3), разрешив их сначала относи-тельно t, а затем, приравняв правые части равенств, имеем:

Если какая – либо координата направляющего вектора равна нулю, то равен нулю и числитель дроби.

26.Угол между прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых.

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами s1 и s2. Так как

т о по формуле для косинуса угла между векторами получим:

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов s1 и s2:

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. L1параллельна L2тогда и только тогда, когда s1 параллелен

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:

28 Условие принадлежности двух прямых одной плоскости

|	x-x1	y-y1	z-z1	|
|	l1	m1	n1	|	= 0
|	l2	m2	n2	|

Если это условие выполняется, прямые или параллельны или пересекаются

41 Координаты вектора в данном базисе

Любой вектор  плоскости единственным образом выражается в виде: , где  – числа, которые называются координатами вектора в данном базисе. А само выражение  называется разложением вектора  по базису

46 Кольцо линейных преобразований Обратное преобразование

Линейные преобразования образуют кольцо линейх преобразований .Между кольцом матриц и кольцом линейных преобразований существует взаимно-однозначное соответствие.Сохраняет свои свойства при сложении и умножении на скаляр.

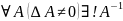
Матрица обратного преобразования является матрицей обратная исходной.

47 Понятие характеристического многочлена и числа Характеристические многочлены подобных матриц

Определение

Для данной матрицы  ,  , где Е — единичная матрица, является многочленом от  , который называется характеристическим многочленом матрицы A(иногда также "вековым уравнением" (secular equation)).

Ценность характеристического многочлена в том, что собственные значения матрицы являются его корнями. Действительно, если уравнение   имеет не нулевое решение, то  , значит матрица   вырождена и ее определитель   равен нулю.