4. Оптические волны в комплексных средах

Изучение комплексных сред или сред с комплексным показателем преломления интересно с теоретической и практической точек зрения. Для современных направлений развития оптики (биомедицина, нанооптика, фотоника) основными изучаемыми и рабочими средами являются комплексные среды. Например, в фотонике все активные оптические среды, на основе которых строятся оптоэлектронные устройства, являются комплексными. В комплексных средах в отличие от идеальных диэлектриков имеет место поглощение света и ряд других особенностей. Эти особенности связаны, прежде всего, с интерференционными эффектами, сопровождающими процесс распространения излучения в таких средах [6].Для практики в комплексных средах интерференционные потоки встречных волн можно использовать для просветления поглощающих слоев конечной толщины.

Отражение и поглощение света в слоистых средах с комплексным показателем преломления

Рассмотрим кратко основные закономерности распространения оптической волны в слоистой среде с комплексным показателем преломления.

Дисперсионное уравнение для распространения световых волн в комплексной среде можно записать, как:

,

где n=n₀-jk – комплексный показатель преломления среды; n₀- показатель преломления для ; k- показатель поглощения; - электропроводность среды; -круговая частота электромагнитной волны; - диэлектрические и магнитные проницаемости среды и вакуума соответственно; c- скорость света электромагнитной волны в вакууме. Реальная и мнимая части показателя преломления связаны между собой, как [7]:

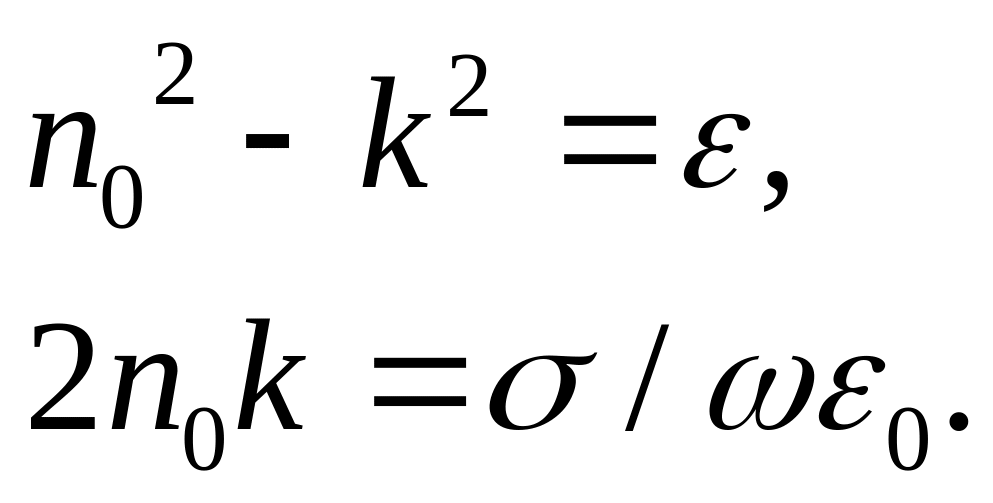
При этом мощность лазерного излучения, проникающая в среду, описывается законом Буггера- Беера-Ламберта:

,

где - показатель поглощения; - длина оптической волны, нм; - коэффициент поглощения, нм^-1.

Пусть оптическая волна падает на границу раздела двух сред под углом и преломляется под углом к оси Z, совпадающей по направлению с нормалью к границе раздела внутри среды. Тогда для TE™ волны с s(p) поляризацией соответственно считается, что электрическая составляющая поля E_x(E_y) перпендикулярна плоскости падения, а вектор H_x(H_y) лежит в плоскости падения волны. Для оптической волны с s(p)- поляризацией коэффициент отражения обозначим как R_n (R_p). Показатель преломления оптической волны в среде выражается через углы падения и преломления с помощью соотношения:

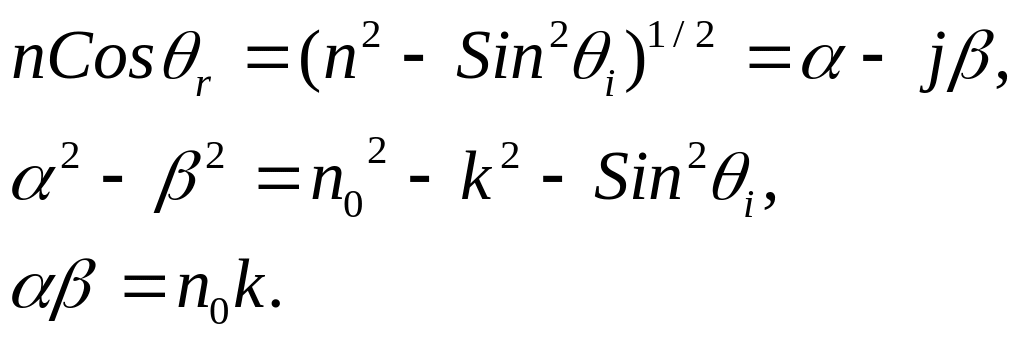(1.38)

Тогда коэффициенты отражения R_n и R_p можно записать как:

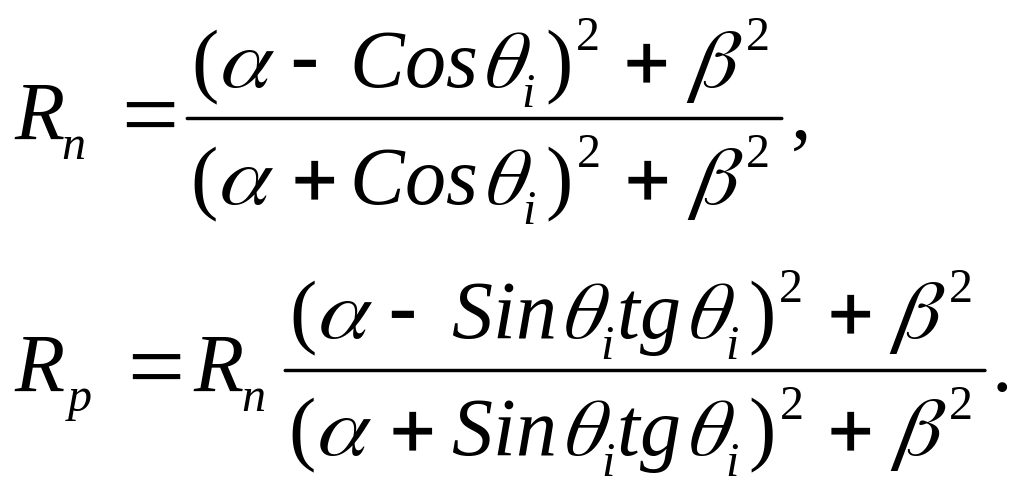(1.39)

Для n₀²>>K² и n₀²>> _{ }значения .

В случае распространения оптической волны внутри более плотной среды под некоторым углом к поверхности раздела сред происходит утечка части энергии этой волны в менее плотную среду. Расстояние h, на котором происходит уменьшение амплитуды волны в e раз, определяется из уравнения, как:

,

где n₁ и n₂ показатели преломления более плотной и менее плотной среды соответственно.

Рассмотрим отражение оптических волн в слое с плоскими параллельными границами. Примером такой среды может служить резонатор Фабри- Перо толщиной в несколько длин волн. На рис. 1.6 показан основной ход оптических лучей в таком слое. Пусть оптическая волна с амплитудой равной единице падает из воздуха на границу резонатора в виде слоя толщиной d. Показатель преломления слоя обозначим, как n₁ . Вторая граница резонатора связана со средой с показателем преломления n₂. Предположим, что n₁>n₂ и изменение фазы происходит только в отраженной волне. Обозначим такой коэффициент отражения , как r₁. Введем следующие обозначения: r₂- коэффициент отражения от нижней границы внутри резонатора; t₁- пропускание через верхнюю границу резонатора; t₂- пропускание из резонатора через нижнюю границу во вторую среду; t₁₁- пропускание волн из резонатора в первую среду.

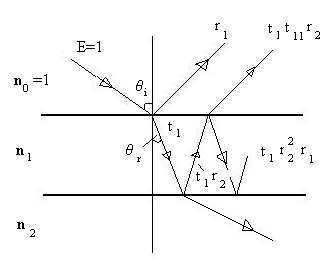
Рис. 1.6. Многократное отражение оптической волны в резонаторе Фабри-Перо

с высоким показателем преломления n₁ (n₁ >n₂>n₀ )

Изменение фазы волны при однократном прохождении слоя определится, как:

(1.40)

где - угол преломления в резонаторе; - толщина слоя.

Считаем, что слой с показателем преломления является поглощающим. Тогда (1.39) можно переписать в виде , где и .

Применяя методику, изложенную в работе [7], коэффициент отражения r и коэффициент пропускания t резонатора Фабри-Перо можно записать, как:

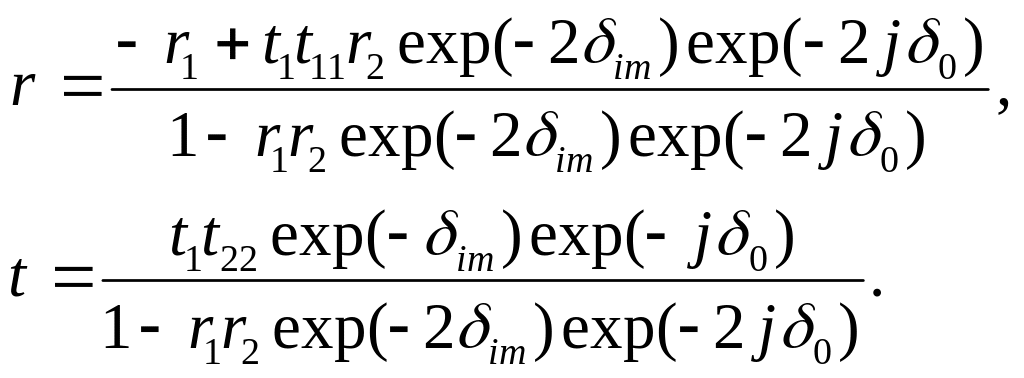(1.41)

Пропускание резонатора максимально, когда разность хода при однократном прохождении оптической волны равно целому числу полуволн, т.е. и . Максимальное отражение имеет место, когда при и , где N=1,2,3,… .

Заметим, что четкость интерференционных полос зависит от степени контраста , т.е. от отношения , где . При наличии поглощения в слое интенсивность света в максимуме и минимуме интерференционной картины меньше, чем для среды без потерь.

Рассмотрим формирование потока оптической энергии, переносимой вне и внутри слоя с комплексным показателем преломления. Переносимая энергия, усредненная за период, в виде вектора Умова-Пойтинга . Для области вне слоя z<0 и z>d получаем . Коэффициенты отражения R и пропускания T определяются , как . Потоки энергии внутри слоя с учетом (1.39) могут быть записаны в виде:

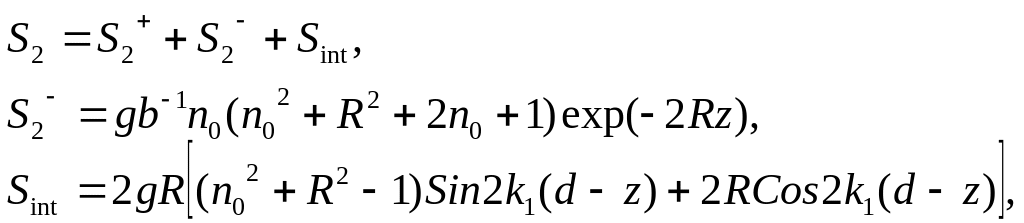(1.42)

где

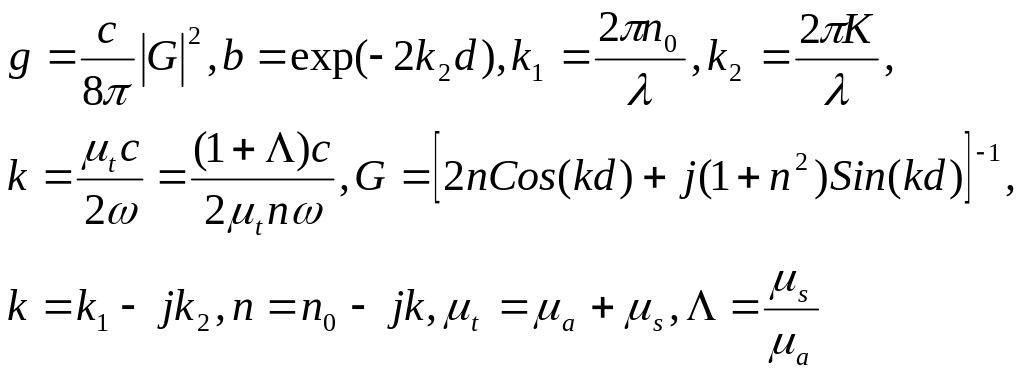
Потоки определяют перенос энергии от одной границы слоя к другой вдоль и против оси z соответственно. Следует отметить особенность формирования интерференционного потока в поглощающей среде двумя встречными потоками в отличие от однонаправленного волнового формирования в среде без потерь. Из соотношений (1.41) следует, что существующий внутри слоя интерференционный поток существенно зависит от потерь энергии оптической волны, связанных с поглощением и рассеянием фотонов в слое. Анализ формирования интерференционного потока показывает, что для тонких слоев с толщиной меньше толщины скин слоя, зависимость S₂(z) практически линейная. С ростом толщины распределение S ₂ (z) становится нелинейной. При z=0 поток S₂ равен сумме потоков падающей и отраженной волны. При z=d поток S₂ равен энергии, прошедшей через слой. Напротив, для толстых слоев вся энергия, переносимая через слой, связана с интерференционным потоком, т.е. S₂(d)=S_int .