
- •Предисловие
- •1. Распространение оптических волн в комплексных и периодических средах
- •1.1. Уравнения Максвелла и граничные условия
- •Гармонические колебания и комплексные амплитуды
- •1.2. Теорема Умова-Пойтинга и законы сохранения
- •1.3. Волновое уравнение и плоские волны
- •Волновые пакеты
- •1.5. Поляризация волн
- •Вектор Джонса
- •Формализм матриц Джонса
- •Оптические волны в комплексных средах
- •Отражение и поглощение света в слоистых средах с комплексным показателем преломления
- •1.7 Оптические волны в периодических средах
- •Одномерные периодические среды
Гармонические колебания и комплексные амплитуды
Как известно
свет можно представить в виде потока
фотонов (квантово - механическое
представление) и в виде волн (волновая
оптика). В таких волнах электрическое
и магнитное поле изменяется по
синусоидальному закону с одинаковой
частотой
![]() .
Однако, здесь мы сразу сталкиваемся с
допущением далеким от действительности.
Дело в том, что область определения
гармонических функций безгранична и
простирается от
.
Однако, здесь мы сразу сталкиваемся с
допущением далеким от действительности.
Дело в том, что область определения
гармонических функций безгранична и
простирается от
![]() до
до
![]() .
Данное допущение не учитывает ограниченных
во времени реальных переходных процессов.
Поэтому гармонические колебания – это
всего лишь математическая модель. А что
же представляют собой реальные сигналы?
Уравнения Максвелла линейны. Поэтому
можно применять преобразования Фурье,
с помощью которых реальный сигнал может
быть представлен в виде линейной
комбинации бесконечного числа
гармонических составляющих. Важно
знать, что каждая гармоническая
составляющая не может существовать
отдельно от гармонического пакета.
.
Данное допущение не учитывает ограниченных
во времени реальных переходных процессов.
Поэтому гармонические колебания – это
всего лишь математическая модель. А что
же представляют собой реальные сигналы?
Уравнения Максвелла линейны. Поэтому
можно применять преобразования Фурье,
с помощью которых реальный сигнал может
быть представлен в виде линейной
комбинации бесконечного числа
гармонических составляющих. Важно
знать, что каждая гармоническая
составляющая не может существовать
отдельно от гармонического пакета.
В произвольной точке пространства компоненты электромагнитного поля (E,H) можно записать в виде:
![]()
Здесь уместно
ввести удобную запись гармонического
колебания в комплексной форме в виде
комплексной амплитуды
![]() .
Поскольку все операторы линейны, можно
оперировать в расчетах с комплексными
амплитудами, в конце вычислений физические
поля определять в виде:
.
Поскольку все операторы линейны, можно
оперировать в расчетах с комплексными
амплитудами, в конце вычислений физические
поля определять в виде:
![]() .
.
Выбор знака в показателе экспоненты – простая условность. В дальнейшем будем брать знак плюс.
На основании выше сказанного уравнения Максвелла в комплексной форме будут выглядеть как:
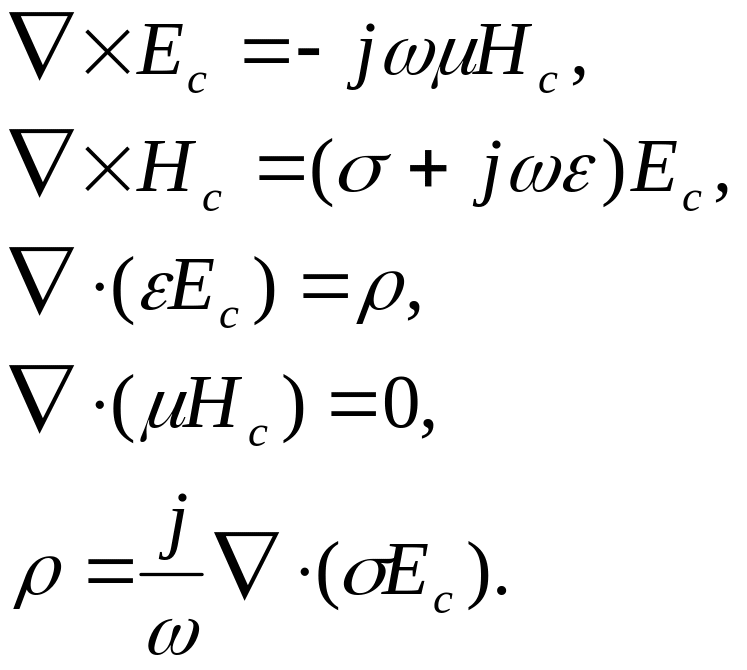 (1.12)
(1.12)
1.2. Теорема Умова-Пойтинга и законы сохранения
Энергия
электромагнитного поля, запасаемая в
единице объема
![]() ,
представляет собой сумму энергии
электрического поля
,
представляет собой сумму энергии
электрического поля
![]() и магнитного поля
и магнитного поля
![]() .
Тогда полную энергию электромагнитного
поля в объеме V
запишем в виде:
.
Тогда полную энергию электромагнитного
поля в объеме V
запишем в виде:
![]() ,
(1.13)
,
(1.13)
где
![]() ,
,
![]() .
.
Энергия
электромагнитного поля W,
запасенная в объеме V
в единицу
времени, может быть затрачена на излучение
из объема и наведение токов проводимости,
если есть в объеме проводники. Потери
на излучение с элемента поверхности
![]() характеризуются
вектором Умова-Пойтинга -
характеризуются
вектором Умова-Пойтинга -
![]() ,
а омические потери – законом Ома -
,
а омические потери – законом Ома -
![]() .
Вектор Умова-Пойтинга определяется как
векторное произведение напряженностей
электрического и магнитного поля.
Физически модуль вектора Умова-Пойтинга
представляет собой интенсивность
излучаемого электромагнитного поля I
(Вт/м2).
Другими словами модуль вектора
Умова-Пойтинга представляет собой
энергию поля, запасаемую в единицу
времени в объеме в виде цилиндра с
площадью основании в 1 м2
и образующей равной
.
Вектор Умова-Пойтинга определяется как
векторное произведение напряженностей
электрического и магнитного поля.
Физически модуль вектора Умова-Пойтинга
представляет собой интенсивность
излучаемого электромагнитного поля I
(Вт/м2).
Другими словами модуль вектора
Умова-Пойтинга представляет собой
энергию поля, запасаемую в единицу
времени в объеме в виде цилиндра с
площадью основании в 1 м2
и образующей равной
![]() м.
м.
![]()
С учетом этих двух механизмов потерь нетрудно записать закон сохранения для электромагнитного поля, запасенного в объеме V в единицу времени, как:
![]() .
(1.14)
.
(1.14)
Средняя по времени электрическая энергия, фиксируемая приемником:
![]() .
.
Составляющие
с частотой
![]() равны нулю. Тогда:
равны нулю. Тогда:
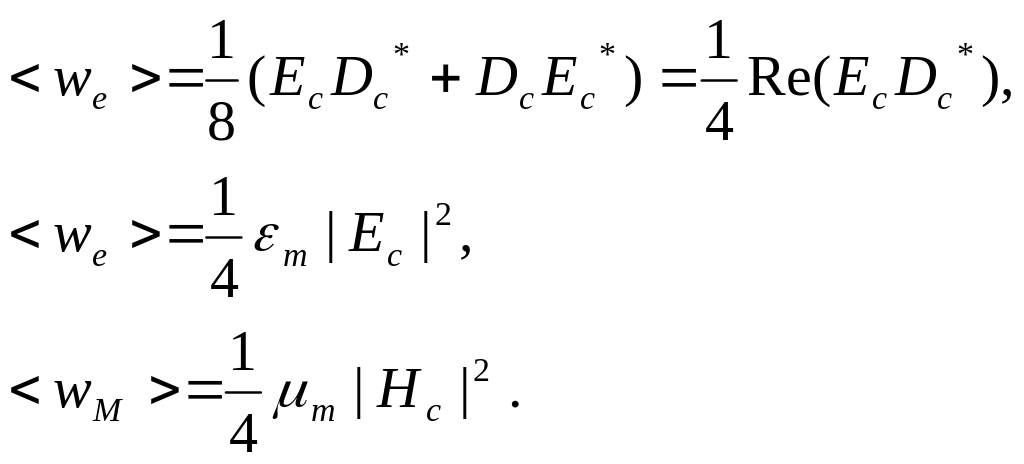 (1.15)
(1.15)
Аналогично для вектора Умова-Пойтинга среднее значение:
![]() .
(1.16)
.
(1.16)
В случае
«идеальной» среды (![]() )
поток вектора Умова-Пойтинга постоянен:
)
поток вектора Умова-Пойтинга постоянен:
![]() (1.17)
(1.17)
Для электрического поля скалярный потенциал U связан с напряженностью электрического поля E:
![]() .
(1.18)
.
(1.18)
Для магнитного поля векторный потенциал A:
![]() .
(1.19)
.
(1.19)
Подставляя (1.19) в (1.2) при M = 0 получим:
![]() .
(1.20)
.
(1.20)
