Анализ простой схемы выхода

При анализе необходимо помнить, что все элементы ЦС имеют конечную добротность и, следовательно, обладают потерями. На рисунке представлена обобщенная простая схема выхода, учитывающая потери в элементах схемы. Для всех элементов схемы, кроме нагрузки, справедливо следующее неравенство

.

Нагрузка этому неравенству не подчиняется. Наиболее удобно нагрузку представить в виде параллельного соединения активной и реактивной составляющих. В конкретной нагрузке соотношение между X_н и может быть любым, т.е.

.

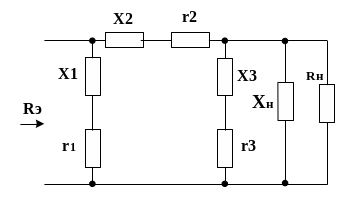
Поскольку X3 и X_н имеют одинаковый знак реактивности, то приведенную схему целесообразно привести к виду, изображенному ниже

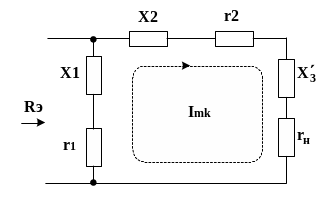
В этой схеме

.

Формулы получены в предположении, что влияние сопротивления потерь элемента на связь нагрузки с контуром ничтожно мало.

Понятие полного сопротивления контура.

Полным сопротивлением контура является сопротивление, полученное при последовательном обходе контура путем суммированием сопротивлений всех элементов

.

Обозначим , .

Наличие в контуре сопротивления говорит о том, что контур нагружен. Если добротность нагруженного контура

,

то входное сопротивление контура в точках подключения АЭ можно рассчитать по формуле

.

После подстановки в формулу соответствующих значений, получим

Для нормальной работы ЦС контур простой схемы выхода необходимо настроить в резонанс.

Если контур настроить в резонанс, обеспечив равенство

,

то входное сопротивление контура будет чисто активной величиной

,

где входное сопротивление контура при холостом ходе. Коэффициент получил название степень связи нагрузки с контуром.

КПД простой схемы выхода при условии ее работы на резонансе рассчитывается по формуле

.

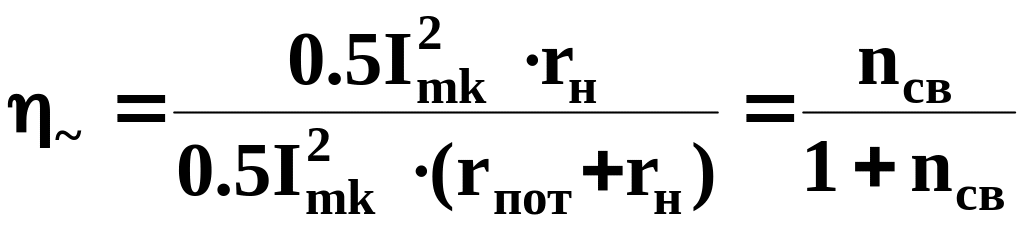На ниже приведенном рисунке представлены графики изменения сопротивления нагрузки на АЭ ГВВ и КПД ЦС при изменении степени связи с нагрузкой и при условии сохранения в контуре резонанса

Из графиков и приведенных формул следует, что, подбирая связь с нагрузкой, можно добиться требуемого согласования ГВВ с оконечной нагрузкой и обеспечить передачу мощности в нагрузку с высоким КПД. Причем КПД ЦС будет тем выше, чем больше будет нагрузочная способность контура ЦС. Под нагрузочной способностью контура ЦС понимают отношение

График зависимости КПД ЦС от степени связи показан на выше приведенном рисунке.

Фильтрующая способность простой схемы выхода

Схемотехническая реализация простой схемы выхода ограничена 6-ю возможными вариантами, из которых 3 схемы используются при емкостном характере нагрузки и 3 схемы – при индуктивном характере нагрузки. Чтобы оценить фильтрующие возможности простой схемы выхода целесообразно остановиться на схеме с наиболее хорошей фильтрующей способностью. Такая схема приведена на рисунке.

Коэффициент фильтрации такой схемы выхода оценивается по формуле

,

где n – номер гармоники, подлежащий фильтрации, Q_хх – добротность ненагруженного контура ( ). В зависимости от рабочей частоты Q_хх принимает значения от 50 до 350 единиц.

Рассмотрим пример. Пусть Q_хх= 200, n = 2, . Коэффициент фильтрации в этом случае будет равен . Это соответствует ослаблению второй гармоники всего на 38 дБ при требовании ГОСТ не менее 60 дБ. Следовательно, простая схема выхода с лучшими фильтрующими способностями не в состоянии обеспечить высоких требований по подавлению гармоник в оконечной нагрузке. По этой причине применение простой схемы выхода в ВУМ весьма ограничено. Чаще одноконтурная резонансная ЦС находит применение в ПУМ, но ее не именуют схемой выхода.