Алгоритм применения необходимых условий экстремума в задаче (23)
Записать систему уравнений Эйлера-Пуассона (24).
Найти общее решение системы (24)
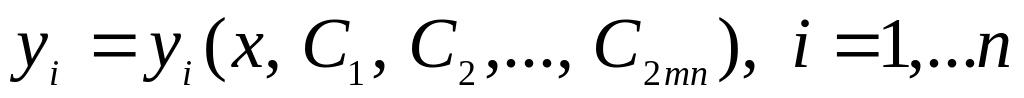.Определить постоянные
из граничных условий и записать выражения
для экстремали
.
Пример. Найти экстремаль функционала
,
удовлетворяющую
граничным условиям:
,
,
,
,
,
,
,
,
,
.
Решение.
Запишем систему уравнений Эйлера-Пуассона.
Учтем, что порядок старшей производной
функции
равен двум, а функции
- трем. Так как
,
,
,
,
,
,
,
,
,
,
,
,
,
,
то получаем
,
.
Решим систему уравнений Эйлера-Пуассона:
,
,
,
,
,
.
Решаем уравнение
.
Заметим, что оно имеет вид
и поэтому может быть переписано в форме
.
Отсюда
.
Обозначим
.
Тогда имеем
,
.
Это линейное неоднородное дифференциальное уравнение. Поэтому сначала решаем соответствующее однородное уравнение:
.
Очевидно, оно является уравнением с разделяющимися переменными:
.
Интегрируя обе части уравнения, получаем
или
.
Решая неоднородное
уравнение, получим решение
.
Переходим к переменной
.
Имеем
.
Отсюда
.
Определим постоянные интегрирования из граничных условий:
,
,
,
,
,
,
,
отсюда
,
.
Находим постоянные
интегрирования
из условий:
,
,
,
.
Имеем:
,
.
Запишем уравнение экстремали
,
.