Теорема 2

Пусть - решение уравнения Эйлера . Если функция имеет непрерывные частные производные до второго порядка включительно, то во всех точках , где функция имеет непрерывную вторую производную.

4. Уравнения Эйлера интегрируются в квадратурах лишь в исключительных случаях. Приведем некоторые простейшие случаи интегрируемости уравнения Эйлера.

Первый случай. Функция не зависит от явно: . Уравнение Эйлера (5) принимает вид и, следовательно,

(7)

Соотношение (7) называется первым интегралом уравнения Эйлера.

Второй случай. Функция не зависит от и явно: . Уравнение Эйлера (6) записывается в форме . Его общее решение имеет вид

(8)

так как а условие дает обыкновенное дифференциальное уравнение первого порядка. Если уравнение имеет один или несколько действительных корней вида то получаем однопараметрическое семейства прямых содержащиеся в двухпараметрическом семействе (8).

Третий случай. Функция не зависит от и явно: или не зависит от явно: . Задача (3) в общем случае решения не имеет, так как уравнение Эйлера (5) принимает вид

(9)

и не является дифференциальным, т.е. его решение не содержит элементов произвола и поэтому не удовлетворяет граничным условиям. Однако, если решение уравнения проходит через граничные точки и , экстремаль существует.

Четвёртый случай. Функция имеет вид .

Уравнение Эйлера записывается в форме

(10)

Это уравнение не является дифференциальным. Его решение удовлетворяет граничным условиям, то экстремаль существует. Если , то под знаком интеграла (2) находится полный дифференциал и, следовательно, величина интеграла не зависит от пути интегрирования, а вариационная задача теряет смысл.

Пятый случай. Функция не зависит от явно: . Уравнение Эйлера (6) имеет вид

,

так как . Если умножить левую и правую части уравнения на , то левая часть превращается в производную .

Поэтому уравнение Эйлера может быть записано в виде и имеет первый интеграл

(11)

Заметим, что часто непосредственное применение уравнения Эйлера (5) оказывается проще использования первых интегралов.

Алгоритм применения необходимых условий экстремума в задаче (3).

1. Найти 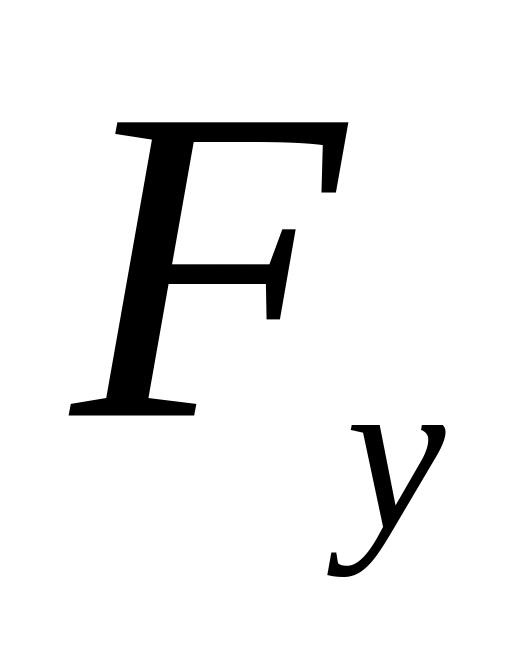, , 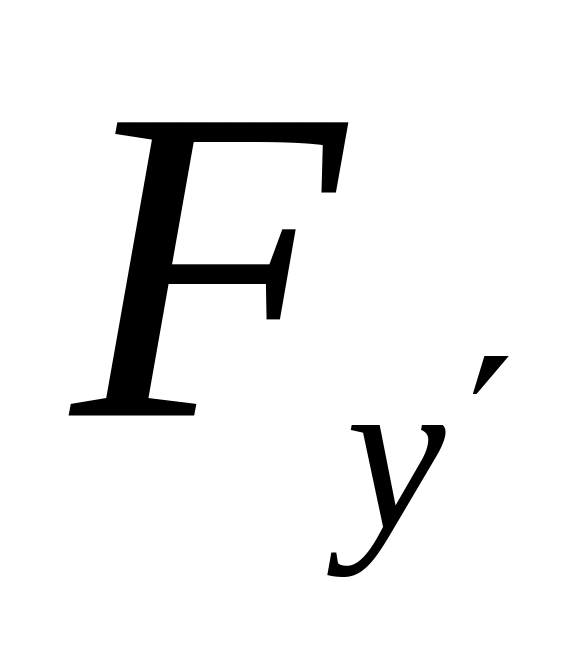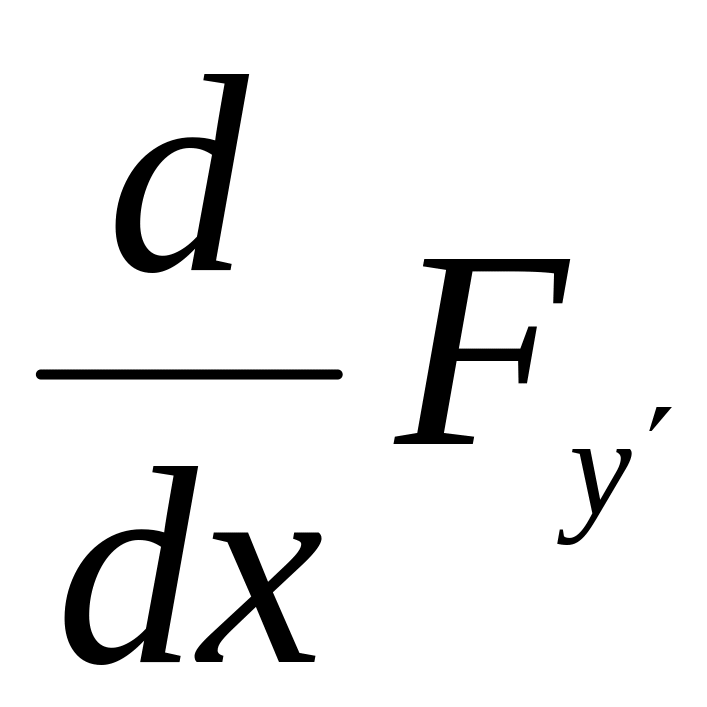и записать уравнение Эйлера

.

Если функция соответствует какому-либо случаю интегрируемости, можно использовать соотношения (7) – (11).

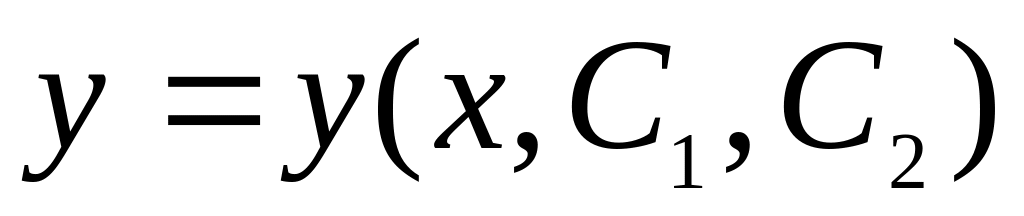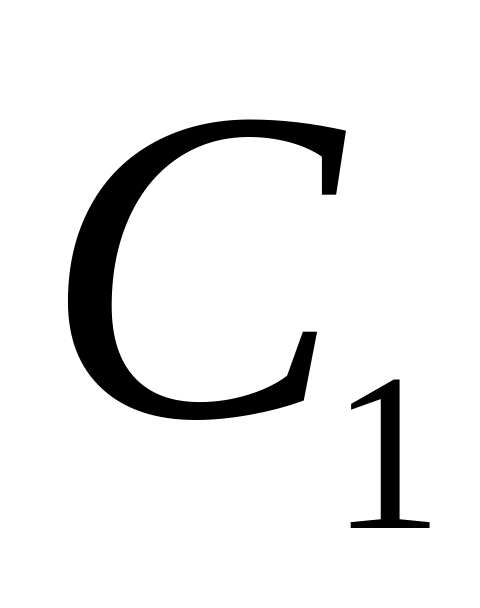2. Найти общее решение уравнения Эйлера , где и 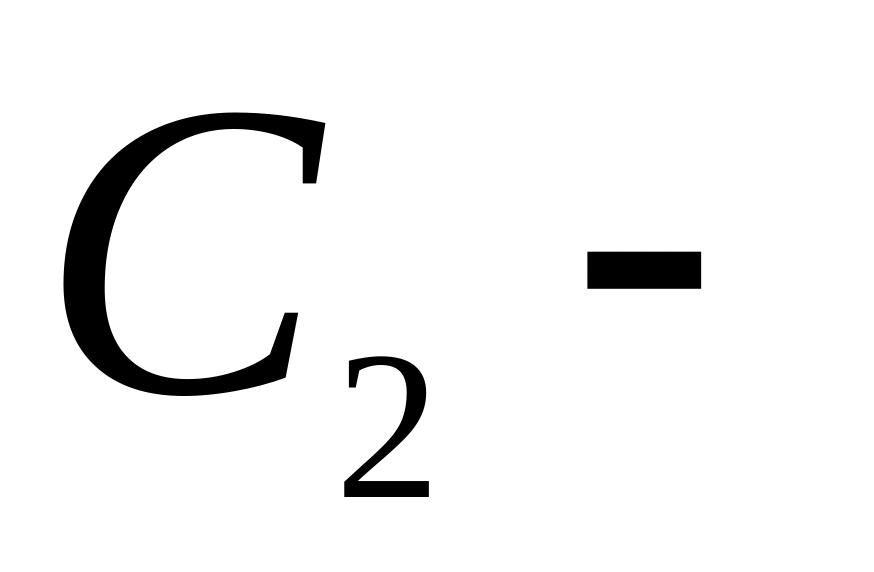произвольные постоянные.

3. Определить постоянные и 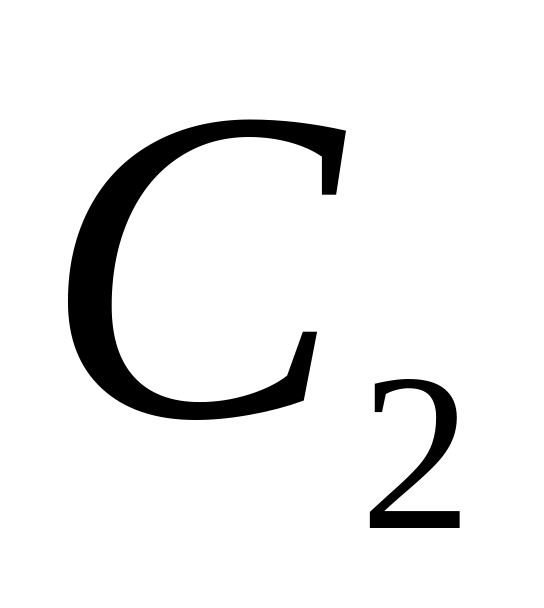из граничных условий, решая систему

В результате получить экстремаль , на которой может достигаться экстремум функционала.

Пример. Найти экстремаль функционала

удовлетворяющую граничным условиям , .

Решение.

1. Запишем уравнение Эйлера (5). Так как , , , , то получаем или .

1. Найдем общее решение уравнения Эйлера. Оно является однородным с постоянными коэффициентами, поэтому составим характеристическое уравнение 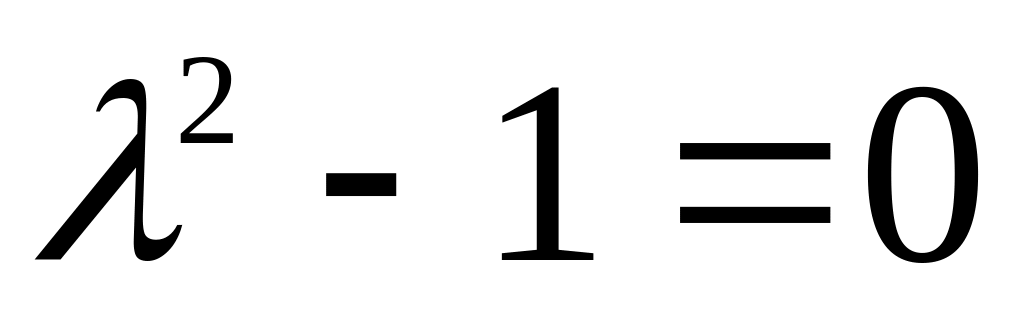. Его корни 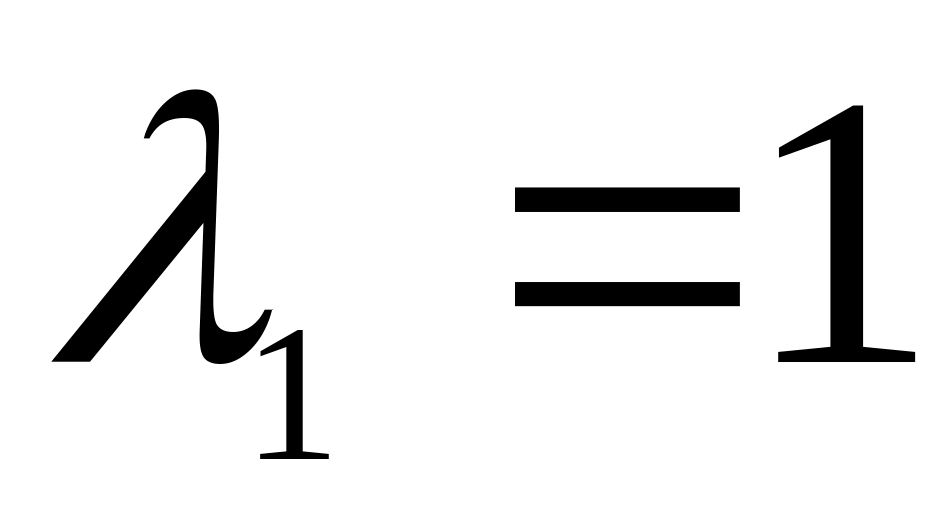, 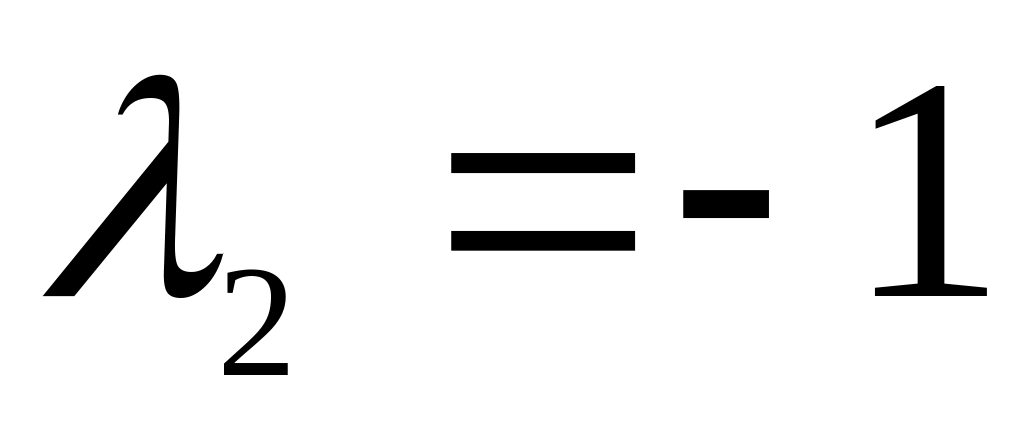- действительные разные. Общее решение однородного уравнения имеет вид

.

2. Определим коэффициенты и из граничных условий:

,

.

Отсюда , . В результате получаем экстремаль .