22

Вариационное исчисление

Вариационное исчисление Понятие функционала

Если каждой функции из некоторого множества поставлено в соответствие некоторое число , то говорят, что на этом множестве задан функционал и пишут . Множество функций , на котором определен функционал , называется областью определения функционала, а число – значением функционала.

Приведем примеры функционалов.

1. Длина плоской кривой, заданной уравнением , :

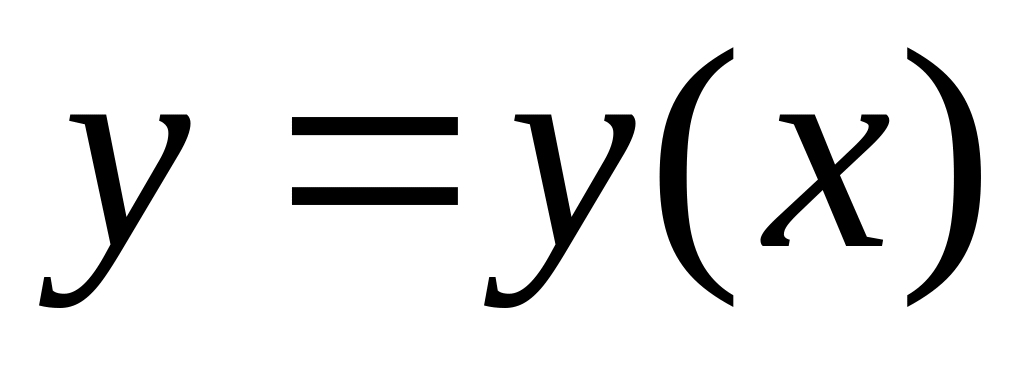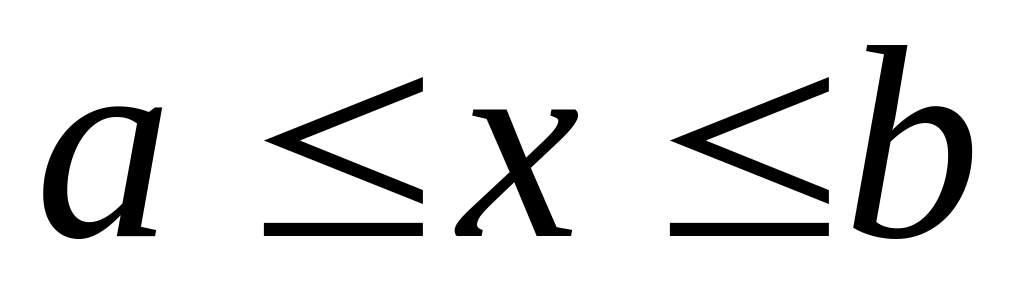2. Вообще, любой определенный интеграл

3. Стоимость проезда по дорогам, имеющим вид кривых, соединяющих пункты А и В.

Основная задача вариационного исчисления – исследование функционалов на экстремум и отыскание тех функций, на которых этот экстремум достигается.

Приведем примеры таких задач.

1. Из всех кривых на плоскости, соединяющих точки А и В, найти ту, которая имеет наименьшую длину.

2. Из различных дорог, соединяющих пункты А и В, выбрать ту, по которой стоимость проезда из А в В минимальна.

Пример. Найти значение функционала на следующих кривых, образующих класс : , , .

Решение. Все кривые проходят через точки , , т.е. удовлетворяют граничным условиям , . Найдем значения функционала, соответствующие каждой кривой из класса :

Функционал называется непрерывным, если малому приращению функции соответствует малое изменение функционала.

Будем полагать, что функционал определен на элементах линейного нормированного пространства функций, в котором каждому элементу поставлено в соответствие действительное число , называемое нормой элемента, при этом выполняются следующие условия:

1. и тогда и только тогда, когда (0 – нулевой элемент).

2. .

3.

для любых элементов , , принадлежащих пространству, и любого действительного числа .

Предметов нашего рассмотрения являются пространства , .

Пространство состоит из непрерывных функций (кривых) , определенных на отрезке . В пространстве норма вводится следующим образом .

Пусть и – произвольное число.

окрестностью нулевого порядка кривой называется совокупность кривых , такая, что

.

Это означает, что расстояние от кривой до кривых мало.

Пространство состоит из непрерывных функций (кривых) , определенных на отрезке и имеющих на этом отрезке непрерывную производную. В пространстве норма вводится следующим образом:

.

Пусть и – произвольное число.

окрестностью первого порядка кривой называется совокупность кривых , такая, что

.

Это означает, что у кривых и кривой близки не только ординаты, но и значения производных. Отсюда следует, что кривая, принадлежащая окрестности первого порядка, принадлежит и окрестности нулевого порядка, но не наоборот.

Аналогично вводится норма в пространстве функций, имеющих производные до порядка включительно, т.е.

.

Пример. Найти расстояния , между кривыми и , в пространствах и .

Решение.

Найдем расстояние в пространстве :

.

Из необходимого условия экстремума получаем и , . Вторая производная в точке отрицательна, поэтому в ней достигается локальный максимум. На концах промежутка функция обращается в нуль. Следовательно, в точке - глобальный максимум и можно подсчитать значение расстояния в этой точке, равное .

Найдем расстояние в пространстве :

.

Так как максимум первого слагаемого уже известен, то исследуем второе слагаемое. Необходимое условие экстремума дает . Так как вторая производная отрицательна, то в точке - локальный максимум. Значение функции на границе равны: 0 и 1, а значение в точке равно . Поэтому максимум функции достигается в точке и равен 1. Отсюда .

Кривые на которых сравниваются значения функционала, называются допустимыми кривыми или кривыми сравнения.

Обозначим через допустимую кривую, на которой функционал достигает экстремума, а через произвольную допустимую кривую. Разность называется вариацией кривой .

Вариация есть функция и принадлежит тому же функциональному пространству, что и функция . Используя вариацию , можно представить любую допустимую кривую в виде

.

Однако используется и другая запись .

В выражении – фиксированная функция, а числовой параметр. Очевидно, что при справедливо .

Назовем приращением функционала разность

.

Линейным функционалом называется функционал , удовлетворяющий следующим условиям:

,

где с – произвольная постоянная, и

.

Если приращение функционала можно представить в виде

,

где - линейный по отношению к функционал, - максимальное значение и при , то главная, линейная по отношению к часть приращения функционала, т.е. , называется первой вариацией функционала.

Можно дать другое определение первой вариации, используя (?)