МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНОЙ РАБОТЕ №1

«ИССЛЕДОВАНИЕ ГЕНЕРАТОРА»

Новосибирск 2008

1 Цель работы

Исследование работы автогенератора:

1. Исследование вольтамперной характеристики электронного прибора;

2. Определение условий возникновения автоколебаний, устойчивости в установившемся режиме работы, частоты и амплитуды автоколебания;

3. Исследование кварца и кварцевого резонатора;

4. Исследование синхронизации автогенератора.

2 Литература

[1] Каганов В.И. Радиотехника + компьютер + MathCAD. М.: Горячая линия - Телеком, 2001г. – С. 94 – 114.

[2] Баскаков С.И. Радио/технические цепи и сигналы. М.: Высшая школа, 2003г. – C. 364 – 378.

3 Порядок выполнения работы

3.1 Исследование вольтамперной характеристики электронного прибора.

3.1.1 Ознакомиться с емкостной и индуктивной принципиальными схемами трехточечных автогенераторов (рисунок 3.1)

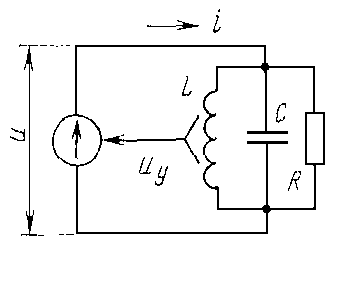
Эквивалентная схема автогенератора

Рисунок 3.1 – Принципиальные схемы автогенератора

3.1.2 Проанализировать вольтамперную характеристику и нелинейную проводимость автогенератора при изменении основных параметров.

Для тока в общей цепи контура запишем

, (3.1)

где - вольтамперная характеристика электронного прибора, т. е. нелинейная зависимость его тока от напряжения.

После дифференцирования (3.1) получим:

, (3.2)

где .. - частота близкая к частоте автоколебаний.

Функцию можно представить в виде суммы членов степенного ряда n-го порядка. Для опреде­ленности примем n=3 и с учетом (3.1) запишем для функции и ее производной:

(3.3)

(3.4)

Подставив (3.4) в уравнение (3.2), после простых преобразований получим обобщенное дифференциальное уравнение, описывающее рабо­ту автогенератора:

(3.5)

где имеем:

, (3.6)

, (3.7)

, (3.8)

, (3.9)

(3.10)

где - волновое сопротивление контура; Q - добротность;

k - коэффициент обратной связи.

Определим коэффициенты, входящие в (3.5). По­скольку есть нелинейная зависимость тока от напряжения, то ее производная есть нелинейная проводимость двухполюсника, которую можно представить в виде:

, (3.11)

где G₀ - отрицательная активная проводимость эквивалентной схемы генераторного диода, подключенного параллельно контуру.

С учетом (3.11) имеем:

(3.12)

(3.13)

(3.14)

3.1.3 Изменить коэффициенты дифференциального уравнения, по заданию преподавателя, в соответствии с таблицей 3.1:

Таблица 3.1 Изменяемые параметры

Номер	а0	а1	а2	а3	G0
1	0	20	0.05	0.1	5
2	3	18	0.03	0.12	8
3	5	15	0	0.15	10

3.1.4 Пример

№1, а0=0, а1=20, а2=0,05, а3=0,1, G0=5

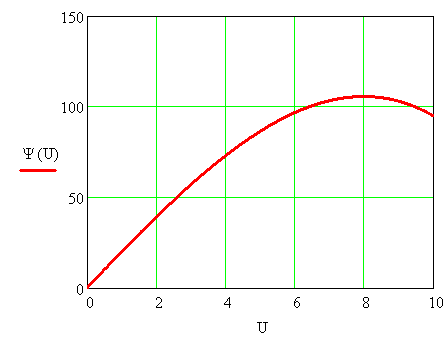
Рисунок 3.2 – Вольтамперная характеристика

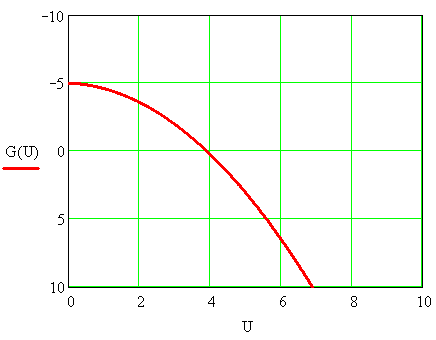
Рисунок 3.3 – Нелинейная проводимость двухполюсника

Наличие в графике (рисунок 3.2) участка насыщения, определяемого нелинейны­ми членами, предотвращает неограниченное возрастание амплитуды ав­токолебаний, что в реальных схемах приводило бы к пробою p-n перехода полупроводникового прибора и выходу его из строя.

3.1.5 Зарисовать полученные характеристики. Характеристики получаются автоматически в соответствии с составленной программой в среде MathCAD.

3.2 Исследование условий возникновения автоколебаний, устойчивости в установившемся режиме, частоты и амплитуды автоколебаний, времени переходного процесса.

3.2.1 Изучить двухконтурную схему автогенератора (рисунок 3.4)

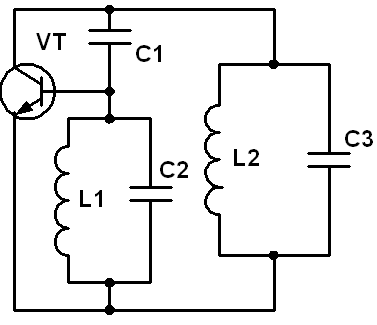
Рисунок 3.4 – Двухконтурная схема автогенератора.

3.2.2 Проанализировать график переходного процесса и его фазовую траекторию.

На основании полученного выше нелинейного дифференциального урав­нения автогенератора составим с помощью математического пакета«Mathсad» программу, позволяющую исследовать работу автогенератора в широком диапазоне изменения его параметров: определять условия возникновения автоколебаний, их устойчивость в установившемся режиме работу, частоту и амплитуду автоколебаний, время переходного процесса.

Заметим, что аналитическое исследование уравнения вида (3.5), называемое уравнением Ван-дер-Поля, возможно только при малом значе­нии параметра (поэтому называют "малым" параметром). Компьютерный метод анализа в среде «Mathсad» позволяет снять данное ограничение и исследовать разно­образные режимы работы автогенератора.

В составляемой программе решение нелинейного диффе­ренциального уравнения (3.5) проводится с помощью метода Рунге-Кутта 4-го порядка путем обращения к функции rkfixed.

Само дифференциальное уравнение 2-го порядка (3.5) записано в программе в виде двух уравнений 1-го порядка:

, (3.15)

где , - функция и ее производная.

В составляемой программе приняты следующие обозначения для нормированного времени или фазы колебаний , функции и ее производной:

, , . (3.16)

Результаты расчета по рассчитываемой программе в виде графика переходного процесса и фазовых траекторий.

3.2.3 Изменить коэффициенты дифференциального уравнения, по заданию преподавателя, в соответствии с таблицей 3.2:

Номер		b	g	Амплитуда
1	0.1	1	0.1	6
2	0.1	1	1	2
3	1	1	0.1	15

Таблица 3.2 Изменяемые параметры

3.2.4 Пример

№1 = 0,1, b = 1, g = 0,1 , амплитуда =6

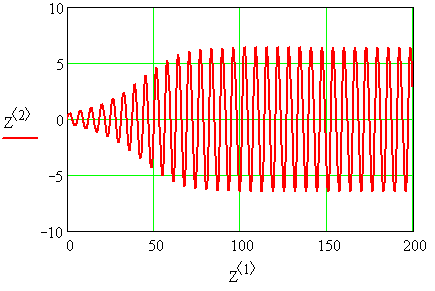
Рисунок 3.5 – График переходного процесса

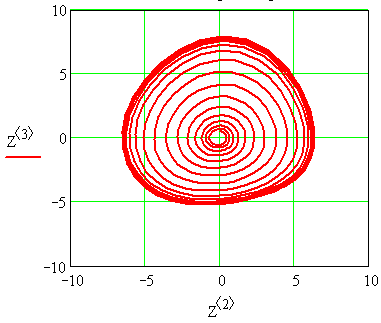
Рисунок 3.6 – Фазовые траектории

3.2.5 Зарисовать полученные характеристики. Характеристики получаются автоматически в соответствии с составленной программой в среде MathCAD.

3.3 Исследование параметров кварца и кварцевого резонатора.

3.3.1 Изучить схемы эквивалентного электрического контура и кварцевого автогенератора (рисунок 3.7)

а)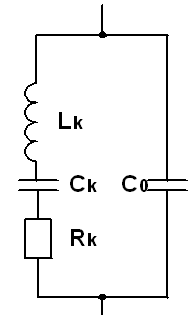 б)

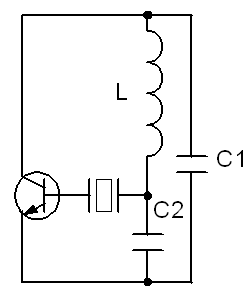
Рисунок 3.7 – а) Эквивалентная схема электрического контура;

б) кварцевой автогенератор

3.3.2 Проанализировать схему электрического контура и кварцевой генератор. Для определения основных параметров и зависимости эквивалентного сопротивления кварца от частоты воспользуемся следующим уравнением:

(3.17)

Для эквивалентного сопротивления кварца из (4.3) получим:

, (3.18)

где С – емкость кварца; L – индуктивность кварца; r – сопротивление кварца; С₀ – емкость резонатора.

3.3.3 Изменить параметры уравнения (3.18) в соответствии с таблицей 3.3:

Таблица 3.3 Изменяемые параметры

Номер	C	L	r	C0
1	0.25	0.2	100	8
2	0.2	0.25	120	10
3	0.2	0.3	125	7

3.3.4 Пример

№1 C = 0.25, L = 0.2, r = 100, C0 = 8

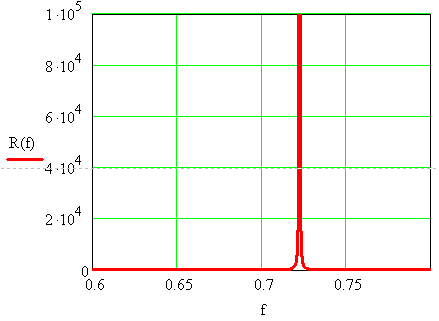
Рисунок 3.8 – Активная составляющая сопротивления

Рисунок 3.9 – Реактивная составляющая сопротивления

Рисунок 3.10 – Фазовый угол

3.3.5 Зарисовать полученные характеристики. Характеристики получаются автоматически в соответствии с составленной программой в среде MathCAD.

3.4. Исследование синхронизации автогенераторов.

3.4.1 Изучить эквивалентную схему диодного СВЧ автогенератора (рисунок 3.11)

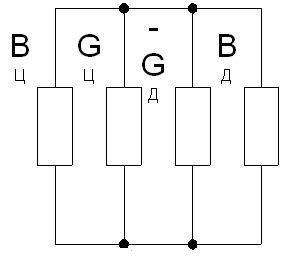
Рисунок 3.11 – Эквивалентная схема диодного СВЧ автогенератора

3.4.2 Проанализировать схему автогенератора. Такой процесс можно представить в виде:

, (3.20)

где , b, g – коэффициенты дифференциального уравнения;

y – начальное условие; U – амплитуда внешнего сигнала;

- нормированная частота внешнего сигнала

3.4.3 В соответствии с таблицей 3.1 изменить параметры

Таблица 3.4 Изменяемые параметры

Номер		b	g		U
1	0.1	0.5	1	1	1
2	0.3	0.25	0.25	4	4
3	0.5	0.3	1	1.5	5

3.4.4 Например

= 0,1; b = 0,5; g = 1; = 1; U = 1

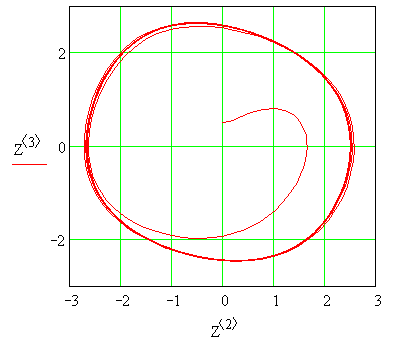
Рисунок 3.12 – Фазовая траектория

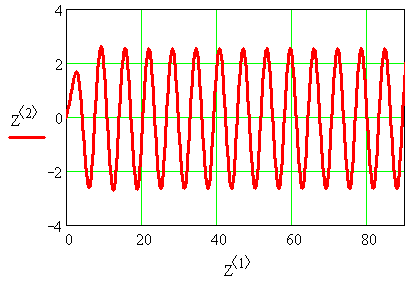
Рисунок 3.13 – Переходный процесс

3.4.5 Зарисовать полученные характеристики. Характеристики получаются автоматически в соответствии с составленной программой в среде MathCAD.

4 Контрольные вопросы

1. Как различают устойчивые и неустойчивые стационарные режимы автогенераторов?

2. Жесткие и мягкие режимы самовозбуждения.

3. Условие самовозбуждения индуктивной трехточки.

4. Почему в автогенераторах в качестве колебательной системы используют кварц?

5. Каким уравнением описывается работа автогенератора в режиме синхронизации?

6. Как, зная вольт-амперную характеристику нелинейного активного элемента, определить границу между мягким и жестким режимами самовозбуждения?

7. Изобразите принципиальные схемы автогенераторов, собранных по схемам индуктивной и емкостной трехточек.

8. От чего зависит устойчивость стационарных режимов?

9. Классификация автогенераторов.

10. Зависимость режима автогенератора от выбора точки.

5 Содержание отчета: Отчет должен содержать: цель работы, исследуемые схемы, графики результатов расчета программы, выводы по полученным результатам.

Приложение 1

1 Режим малого сигнала

Часто в активных радиотехнических цепях возникают периодические автоколебания. Так принято называть колебательные процессы, существующие без внешнего периоди­ческого воздействия. Устройства, генерирующие автоколебания, называют автоколебательными системами, или автогенераторами. Работа любого автогенератора основана на том, что энергия от источника питания через управляемый элемент, например транзистор, подается в колебательную систему. Сигнал, управляющий транзистором, с этой же колебательной системой и подается на электрод транзистора через цепь обратной связи.

При соответствующем выборе параметров такая система становится неустойчивой. Амплитуды любых малых колебаний, вызванных, например, тепловыми шумами, неограниченно возрастают. Однако по мере роста амплитуды, существенную роль начинают играть нелинейные свойства управляемого элемента. Это ведет к тому, что амплитуда автоколебаний достигает некоторого установившегося значения и в дальнейшем остается практически постоянной, Говорят, что при этом автогенератор работает в стационарном режиме.

При анализе и расчете автогенераторов возникают две основные задачи:

1) выяснить, при каких условиях устройство с обратной связью становится неустойчивым, т.е. само возбуждается;

2) определить амплитуду и частоту автоколебаний в стационарном режиме.

Первую из этих задач решить относительно несложно, поскольку при малых амплитудах автоколебаний на начальном этапе процесса нелинейный управляемый элемент может быть эквивалентно заменен линейной схемой замещения. Намного сложнее решить вторую задачу, состоящую в исследовании системы с обратной связью при условии, что нелинейными эффектами пренебречь нельзя.