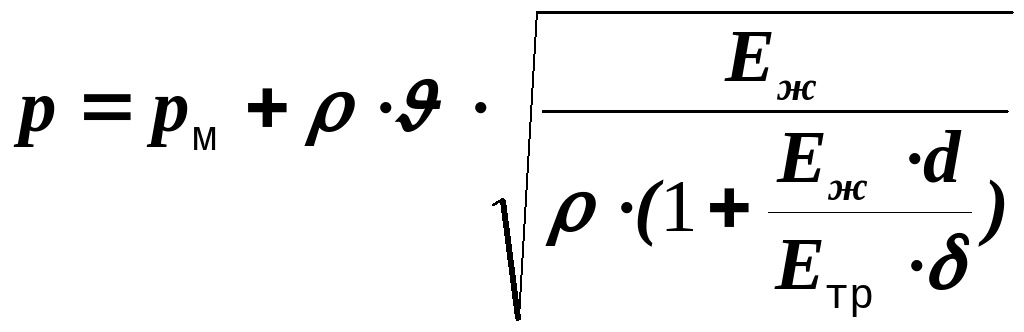3.2. Определение максимального расхода жидкости во всасывающем трубопроводе

Определим максимально возможный расход жидкости во всасывающем трубопроводе заданного диаметра d = 200 мм (пример 1.4) из условия отсутствия кавитации. Для этого в уравнении Бернулли (51) обозначим:

(52)

Уравнение (52) решено графическим способом с помощью Microsoft Excel.

расход Q	0,00001	20	40	60	80	100	120
число Re	1,08E-01	2,16E+05	4,32E+05	6,48E+05	8,64E+05	1,08E+06	1,30E+06
l	5,51E-01	2,53E-02	2,50E-02	2,49E-02	2,48E-02	2,48E-02	2,47E-02
f(Q)	0,00	0,25	0,98	2,21	3,93	6,13	8,83

Определение максимального расхода во всасывающем трубопроводе

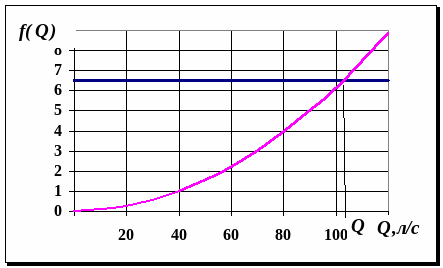
Рис.27.

Из Рис.27 следует, что Q_max=104 л/с.

3.3. Определение максимального коэффициента сопротивления фильтра или максимально возможной высоты всасывания

Анализируя уравнение (51), замечаем, что при заданных значениях параметров Q и d давление на входе в насос может стать меньше давления насыщенного пара при условии, если:

1. Высота всасывания h_вс превысит допускаемую ;

2. Засорится фильтр 4 и коэффициент сопротивления фильтра превысит свое предельно возможное значение.

Расчет предельных значений h_вс или z_ф производится непосредственно по уравнению (51) при р₂=р_н.п. и не вызывает затруднений.

Глава 4
	Расчеты на прочность элементов гидравлической сети

Гидравлическая сеть представляет собой систему трубопроводов и резервуаров, соединенных между собой определенным образом. Стенки трубопроводов, равно как и стенки закрытых резервуаров, могут находиться под действием высоких избыточных давлений. При этом возникают большие разрывающие усилия, которые могут превысить предельно допускаемые для данной конструкции из условий прочности.

Для предотвращения аварийных ситуаций необходимо прогнозировать максимально возможные давления в системе и определять предельные значения конструктивных элементов гидравлической сети. В данном разделе показано, как это делается.

4.1. Определение минимальной толщины стенки из условия прочности при гидравлическом ударе

На практике в трубопроводе возможно резкое повышение давления (гидравлический удар) вследствие внезапного торможения движущейся в нем жидкости. Это явление возникает, например, при быстром закрытии различных запорных устройств, устанавливаемых на трубопроводах (задвижка, кран), клапанов, внезапной остановке насосов, перекачивающих жидкость и др. Гидравлический удар может привести к повреждениям мест соединения отдельных труб (стыки, фланцы), разрыву стенок трубопровода, поломке насосов.

Повышение давления при гидравлическом ударе определяется по формуле Н. Е. Жуковского :

Dр = r× с×J ,

(53)

где: r - плотность жидкости, J - скорость движения жидкости в трубопроводе до удара, с - скорость распространения волны гидравлического удара.

,

(54)

где: E_ж - модуль упругости жидкости (справочная величина, Приложение 6), E_тр - модуль упругости материала стенок трубопровода (Приложение 7), d- внутренний диаметр трубопровода, d- толщина стенки трубопровода.

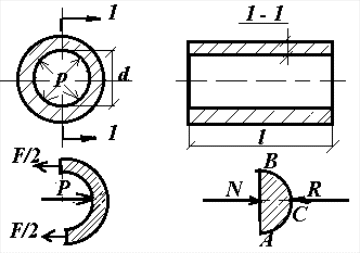
При резком закрытии крана 5 на напорном трубопроводе (Рис.13) происходит гидравлический удар, и давление р перед краном становится равным:

р = рм +Dр

(55)

где р_м - давление на выходе из насоса в момент удара, Dр - повышение давления при гидравлическом ударе.

Определим разрывную силу P, которая будет действовать на стенки трубопровода при гидравлическом ударе. Для этого рассмотрим равновесие жидкости в объеме полуцилиндра ABC (Рис.28).

Иллюстрация к расчету толщины стенки трубопровода

Условие равновесия жидкости в объеме полуцилиндра ABC: R = N, где R - реакция полуцилиндрической поверхности ABC. Она равна по величине и противоположна по направлению искомой разрывающей силе P. N - реакция сжатой жидкости, находящейся слева от поверхности AB.

Рис.28.

Сила N равна силе давления жидкости на поверхность прямоугольника с размерами d, l.

Учитывая, что N=p×d×l , получим:

R =N= P = p×d×l

(56)

Разрывающая сила P вызывает появление силы сопротивления F в материале стенки трубопровода и внутренних растягивающих напряжений, связанных с силой F следующим уравнением:

F = s× 2× d × l

(57)

В момент разрыва s = [s ] - допускаемому напряжению на разрыв, а толщина стенки d при этом минимальна, d = d_min.

Приравнивая в этой ситуации силы P и F, получим:

p×d×l = [s]× 2× dmin × l ,

откуда:

dmin = p×d / 2[s]

(58)

Из зависимостей (53), (54) и (55) имеем:

(59)

Подставляя (59) в (58), получим уравнение для определения d_min:

(60)

Зависимость (60) есть трансцендентное уравнение относительноd_min.

Это уравнение можно решить графическим способом или с помощью ЭВМ одним из известных численных методов (итераций, половинного деления и др).

Графический способ подробно изложен в Разделе 3. Здесь покажем, как решается трансцендентное уравнение на ЭВМ методом итераций.

Для использования этого метода необходимо представить исходное уравнение в виде: параметр равен функции от параметра. Уравнение (60) уже имеет такой вид: d = f (d).

Графическое изображение левой и правой частей уравнения (60) показано на Рис.29.

Иллюстрация метода итераций

1.Задаемся любым значением параметра d, например, dн . 2. Определяем при этом значении параметра значение функции f( dн ). 3. Присваиваем значение функции значению параметра d1. 4. Находим при d1 значение f( d1) и так далее до тех пор, пока последующее и предыдущее значение функции не совпадут с заданной точностью.

I - изображение левой части уравнения (60)- f_л = d ; 2 - изображение правой части уравнения (60)- f_пр = f( d); d ₀- решение уравнения (60).

Рис.29.