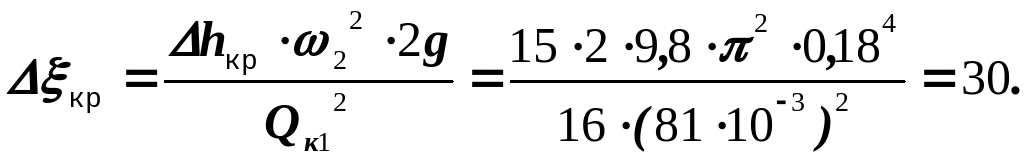2.1 Изменение характеристики сети

Уменьшить подачу насоса можно при более крутой характеристике

сети, а увеличить при более пологой характеристике сети.

На практике чаще всего уменьшают подачу насоса, закрывая кран на напорной магистрали. При открытии крана подача насоса увеличивается (характеристика сети становится более пологой).

Если кран открыт полностью и диапазон регулирования с его помощью уже исчерпан, можно присоединить к трубопроводу параллельно еще одну трубу (лупинг), при этом гидравлическое сопротивление системы уменьшается, а расход в сети увеличивается.

2.1.1. Расчет коэффициента сопротивления регулировочного крана Постановка задачи

Для примера расчета, изложенного в разделе 1.4, определить степень

открытия крана 5, при которой расход жидкости в системе уменьшается на 10 %

Решение задачи заключается в вычислении коэффициента сопротивления крана. Затем из Приложения 9 можно определить степень его открытия.

Последовательность решения задачи.

1. Определяем необходимый расход жидкости в системе и отмечаем на характеристике насоса новую рабочую точку К₁ (Рис.16).

Q_к1 = Q_к × 0,9 = 90×10^-3 ×0,9 = 81×10^-3 м³/с.

К определению коэффициента сопротивления крана

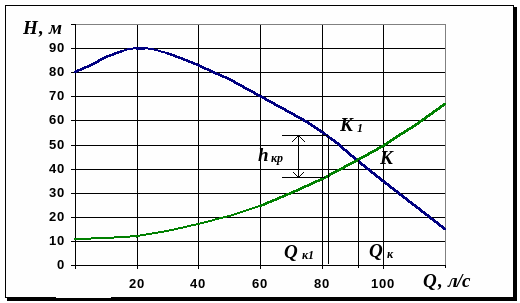
Рис.16.

2. Определяем по графику величину дополнительных потерь напора в кране при его закрытии: Dh_кр= 15м.

3. Определяем дополнительный коэффициент сопротивления крана при его закрытии из формулы Вейсбаха:

Откуда:

4.0пределяем суммарный коэффициент сопротивления крана:

xкрå =Dxкр + xкр =30 +2 =32.

Отметим, что перед регулированием системы на новый расход кран

уже был частично закрыт, и его коэффициент сопротивления был равен

двум.

5. Используя Приложение 9, определяем степень открытия n крана, при которой в данной сети будет проходить расход Q_к1 . Для этого строим график зависимости x_кр =f(n). Из Рис.17 следует, что при x_кр =30 степень открытия n =0,22.

Определение степени открытия крана

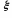
Рис.17.

2.1.2. Расчет параметров лупинга

Лупинг - вспомогательный трубопровод, присоединяемый параллельно к основному трубопроводу на некоторой длине l₂ (Рис. 18).

Название лупинга происходит от английского слова loop, что означает петля.

Иллюстрация к расчету параметров лупинга

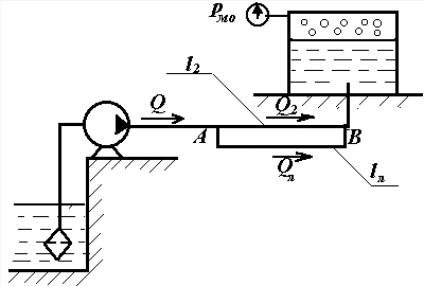
Рис.18.

Пусть к участку АВ нагнетательного трубопровода присоединен лупинг длиной l_л и диаметром d_л. При этом расход жидкости Q, который перемещался по нагнетательному трубопроводу, в точке А разделяется на две в общем случае неравные части Q₂ и Q_л , причем Q₂+ Q_л = Q_..

Закон сохранения энергии, примененный последовательно к сечениям А и В основного трубопровода и лупинга, имеет вид:

	- для основного трубопровода
	- для лупинга

Поскольку в одной точке не может быть двух разных давлений, то:

(рА - рВ )2 =(рА - рВ )л

Следовательно: потери напора на участке основного трубопровода равны потерям напора в лупинге.

При определении потери энергии на единицу веса (потери напора) для всего нагнетательного трубопровода необходимо определить потери напора на разветвленном участке АB:

Таким образом:

При определении потерь напора в нагнетательном трубопроводе с параллельными участками в уравнение Бернулли следует подставлять потери напора только в одном параллельном участке.

Вследствие того, что расход на участке нагнетательного трубопровода длиной l₂ стал меньше, потери на этом участке уменьшились и, следовательно, уменьшились потери напора на всем трубопроводе. При этом характеристика сети (Рис.19) стала более пологой и расход в системе увеличился.