1.5 Область пространства, существенная при ррв

Областью пространства, существенной при РРВ, называют область, в которой распространяется основная часть передаваемой мощности сигнала.

Эта область играет определяющую роль при РРВ. Для определения существенной области обратимся к известному принципу волновой оптики – принципу Гюйгенса – Френеля.

Согласно этому принципу каждую точку на произвольно замкнутой поверхности охватывающей излучатель , можно считать источником вторичных сферических волн, а поле в точке можно определить в результате векторного суммирования полей от всех вторичных излучателей (рис. 1.3)

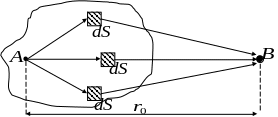
Рисунок 1.3

Границы существенной области пространства проще всего определить, рассмотрев случай дифракции сферической волны на круговом отверстии в бесконечном экране с использованиям принципа Гюйгенса- Френеля (рис.1.4).

Экран - бесконечно больших размеров. Экран радионепрозрачный, т.е. ЭМВ через него не проходят. Экран выбран в качестве поверхности, на которой рассматриваются вторичные элементарные излучатели.

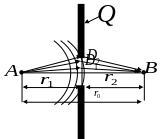
Рисунок 1.4 – Сечение экрана плоскостью проходящей через линию

В экране сделаем отверстие радиусом с центром по линии . Напряженность поля в точке определяется результатом векторного суммирования полей элементов Гюйгенса, находящихся только в пределах отверстия.

Если отверстия в экране нет, то из-за бесконечных размеров и непрозрачности поле в точке будет равно нулю.

Проделаем теперь отверстие в экране площадью . За счет излучения вторичных излучателей на поверхности в точке появится некоторая напряженность поля , имеющая модуль и фазу .

Последовательно увеличивая отверстие, получим векторную диаграмму рис.1.5.

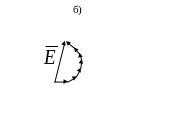
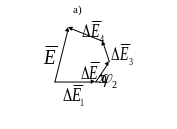
Рисунок 1.5 – Геометрическое суммирование полей от различных участков отверстия при скачкообразном (а) и плавном (б) изменении его диаметра.

Рисунок 1.6- Векторная диаграмма при диаметре отверстия, соответствующего первой зоне Френеля.

По мере увеличения площади отверстия наступит такой случай, когда поля от вторичных источников периферийной линии отверстия окажутся в противофазе с полем, обусловленным вторичным излучением центра отверстия. Это как видно из рис.1.4 будет соответствовать разности хода .

Отверстие, при котором удовлетворяется это условие, носит название первой зоны Френеля. При этом напряженность поля в точке получается наибольшим.

При дальнейшем увеличении площади отверстия напряженность поля в точке начнет уменьшаться вследствие того, что поля от вновь получаемых кольцеобразных поверхностей отверстия будут уже в противофазе с полями, обусловленными излучением кольцеобразных поверхностей первой зоны Френеля (рис. 1.7). Это соответствует второй зоне Френеля. Разность хода при этом . Напряженность поля в этом случае минимальна.

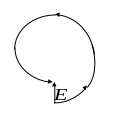
Рисунок 1.7 – Векторная диаграмма, соответствующая второй зоне Френеля.

Если плавно увеличивать площадь отверстия и дальше, то получим векторную диаграмму в виде закручивающейся спирали (рис.1.8).

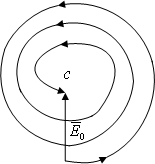
Рисунок 1.8

Спираль закручивается вокруг точки . Вектор , соединяющий начало спирали с точкой будет равен напряженности поля при отсутствии экрана. Максимальные и минимальные значения напряженности поля в точке будут при выполнении условия

(1.25)

где - целое число. При - нечетных будет максимум, при - четных – минимум.

Отсюда следует, что напряженность поля в точке приема носит осциллирующий характер. Это можно проиллюстрировать с помощью рис.1.9.

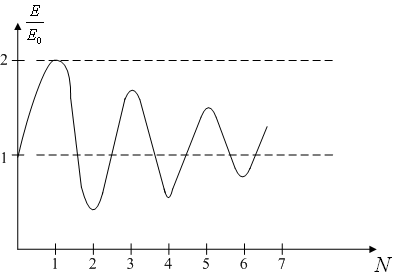
Рисунок 1.9

На рис. 1.9 - номер зоны Френеля. В нечетных зонах Френеля напряженность поля выше, чем в четных. Знание такой закономерности позволяет правильно выбрать высоты подвеса приемной и передающей антенны. На плоскости существенная область представляет собой эллипс с фокусами в точках и (рис. 1.10).

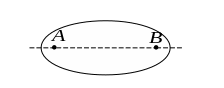
Рисунок 1.10

Существенная область пространства в однородной среде представляет собой эллипсоид вращения с фокусами в точках и . Существенной областью считают ту, что охватывает (8…12) зон Френеля. Поперечное сечение существенной области представляет собой круг радиусом .

Кроме существенной области и области первого эллипсоида Френеля при расчете радиолиний используется понятие минимальной области распространения радиоволн. При этом .

Поперечные размеры минимальной области определяются радиусом соответствующей минимальной зоны .

, (1.26)

где - длина волны;

- относительная координата препятствия ( или );

- расстояние между точками передачи и приема (рис.1.11).

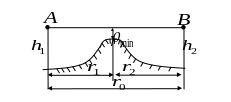Рисунок 1.11

Для обеспечения устойчивой связи необходимо выбрать высоты подвеса антенн и такими, чтобы просвет между наивысшей точкой препятствия и линией был больше или равен .