1.3 Выбор и обоснование схемы ракеты

Выбор схемы ракеты предусматривает решение следующих задач:

– выбор типа двигателя;

– выбор типа старта;

– выбор конструктивно-компоновочной схемы;

– выбор конструкторских материалов;

– выбор программы полета;

– выбор проектных параметров.

Тип двигателя существенно влияет на конструкцию ракеты в целом. Наиболее широкое применение тактических и оперативно-тактических ракет находят в настоящее время ракетные двигатели твердого топлива. Этот тип двигателя по сравнению с жидкостными двигателями обладает следующими достоинствами: простота конструкции; надежность и безотказность; постоянная готовность к действию; простота эксплуатации.

Исходя из этого в дипломной работе предпочтение отдано твердотопливному ракетному двигателю.

Тип старта во многом предопределяет конструкцию пусковой установки, а так же влияет на конструкцию и характеристики ракеты. Для неуправляемых баллистических ракет может применяться только наклонный старт, для управляемых – как наклонный, так и вертикальный. Влияние типа старта на конструкцию ракеты проявляется через схему ее нагружения при старте, через устройство узлов взаимодействия ракеты с направляющей. Кроме того, тип старта в значительной степени предопределяет значение начальной тяговооруженности n₀. При наклонном старте тяговооруженность двигателя должна быть больше, чем при вертикальном старте.

Для проектируемой ракеты целесообразно выбрать наклонный старт, т.к. дальность пуска составляет 310 км, откуда напрашивается вывод о том, что масса проектируемой ракеты будет незначительной.

К онструктивно-компоновочная схема влияет на массовые и геометрические характеристики ракеты, находя отражение в коэффициентах весовых уравнений.

При выборе ККС необходимо принять решение о количестве ступеней, способах установки составных частей ракеты, типе органов управления, например для управляемой ракеты системы разделения ступеней и отделения БЧ и пр.

Количество ступеней ракеты во многих случаях принимается априорно. Для ракет с дальностью пуска до 500 км применяется, как правило, одноступенчатая схема ракеты. Функциональное назначение отсеков ракеты, а для твердотопливной ракеты таковыми являются БЧ, приборный отсек, двигательная установка с РДТТ, хвостовой отсек, а также органы управления и стабилизации, предопределяет их взаимное расположение.

Факел пламени, вытекающий из ракетного двигателя, вынуждает располагать выходной (сопловой) блок двигателя в заднем (т.е. хвостовом) отсеке. Таким образом, часто при выборе ККС приходиться решать вопрос о взаимном расположении БЧ и приборного отсека.

Принципиально возможно и допустимо переднее расположение приборного отсека. Тогда его корпус должен иметь коническую или коническо-цилиндрическую форму. Однако с целью уменьшения инерциальных нагрузок, усложняющих работу чувствительных элементов приборов СУ, последние целесообразно располагать вблизи ЦМ ракеты. Для этого наиболее целесообразным является расположение приборного отсека за БЧ. Чаще всего для твердотопливной УБР с одной ступенью используется следующая компоновка: БЧ – приборный отсек – двигательная установка – хвостовой отсек. При этом часть приборов СУ размещается в хвостовом отсеке. Для проектируемой ракеты выбрана аналогичная ККС, представленная на рисунке 1.2.

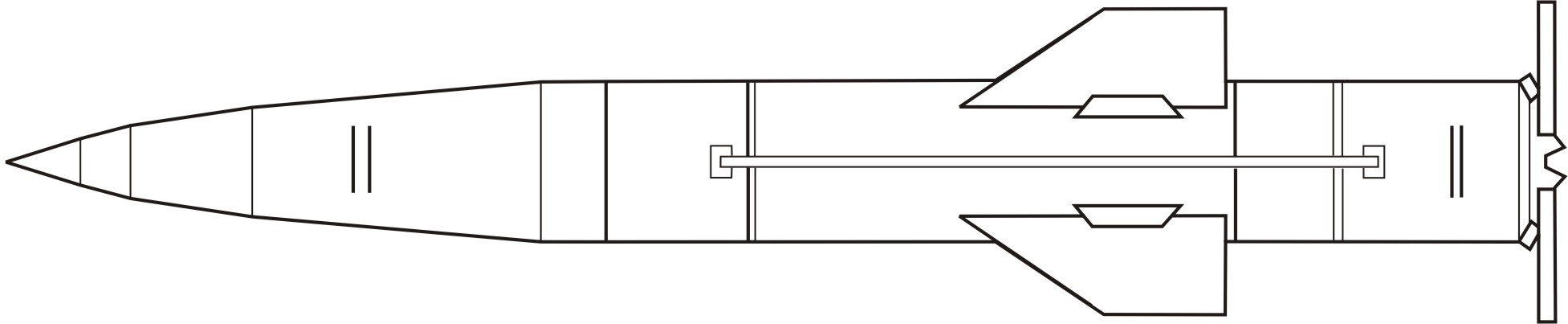
Рисунок 1.2 – Конструктивно-компоновочная схема проектируемой ракеты

Органы управления могут выполняться в виде аэродинамических и газодинамических рулей, отдельных рулевых двигателей, а также поворачивающихся или разрезных сопел и др. В качестве органов управления проектируемой ракеты выбираем газодинамические рули.

Несмотря на то, что отделяемая в полете БЧ за счет введения системы отделения усложняет конструкцию ракеты и снижает ее надежность, при дальности пуска более 300 км просто необходимо применять вариант ракеты с отделяемой БЧ. Эта необходимость диктуется в основном зависимостью величин аэродинамических и тепловых нагрузок пассивного участка траектории от дальности полета.

Известно, что чем больше дальность полета, тем большую скорость должна иметь ракета в конце активного участка траектории. В этом случае в плотные слои атмосферы на пассивном участке ракета будет входить с большей скоростью (относительно скорости активного участка траектории), а аэродинамические нагрузки, которые действуют на ракету в процессе ее полета в плотных слоях атмосферы, пропорциональны квадрату скорости.

Для схемы ракеты с отделяющейся БЧ корпус ракетной части должен быть рассчитан на максимальные нагрузки активного участка траектории. Они мало зависят от дальности полета (ракета плотные слои атмосферы проходит примерно с одной и той же скоростью и разгоняется до требуемой скорости уже в разреженных слоях). В итоге, несмотря на то, что система отделения обладает собственной (т.е. дополнительной) массой, стартовая масса такой ракеты с большей дальностью полета оказывается меньше по сравнению с ракетой меньшей дальности с неотделяемой БЧ в своем составе.

Т аким образом, можно сделать вывод о том, что при значительных дальностях полета отделение БЧ не только целесообразно, но и необходимо.

Выбор материала конструкции является важным шагом поиска конструктивного решения, поскольку от выбора материала зависят массовые, технологические, эксплуатационные и другие свойства конструкции. При выборе материала необходимо учитывать следующие факторы:

– массовые и простые характеристики;

– свариваемость;

– пластичные свойства;

– антикоррозийные свойства;

– недефицитность и стоимость.

Перечисленные свойства не всегда оптимально сочетаются в одном материале, поэтому, в зависимости от назначения конструктивного элемента, для которого осуществляется выбор материала, выделяют определенные требования, выполнение которых должно быть обеспечено в первую очередь.

Как правило, определяющим требованием является требование минимальной массы при условии обеспечения неразрушимости конструкции под действием эксплуатационных нагрузок. Можно показать, что данное требование предопределяет выбор материала с высоким значением:

– удельной прочности для отсеков ракеты с наиболее вероятным разрушением из-за потери прочности (например, камера РДТТ);

– удельной жесткости для отсеков ракеты с возможной потерей устойчивости (общей или местной).

В настоящее время для изготовления отдельных частей корпуса ракеты находят применение высокопрочные стали различных марок, алюминиевые и титановые сплавы, а также композиционные материалы (стеклопластик, углепластик, органопластик, боропластик, боролюминий). Поэтому для проектируемой ракеты выбраны материалы, перечень (с основными механическими свойствами) которых приведены в таблице 1.1.

Таблица 1.1 – Основные механические свойства некоторых конструкционных материалов при нормальной температуре

Материалы	Марка	Характеристики
		GB, МПа	Е, ГПа	, кг/м3	, Нмкг	, Нмкг
Сталь	4340	1950	203	7800	250	26,0
Алюминиевые сплавы	В95Т	700	71	2700	259	26,3

Выбор приближенной программы движения управляемой баллистической ракеты является одной из частных задач баллистического проектирования.

Под программой полета понимается одна из зависимостей

, или ,

где , , углы тангажа, наклона вектора скорости и атаки соответственно, которые связаны между собой очевидным соотношением (рисунок 1.3)

.

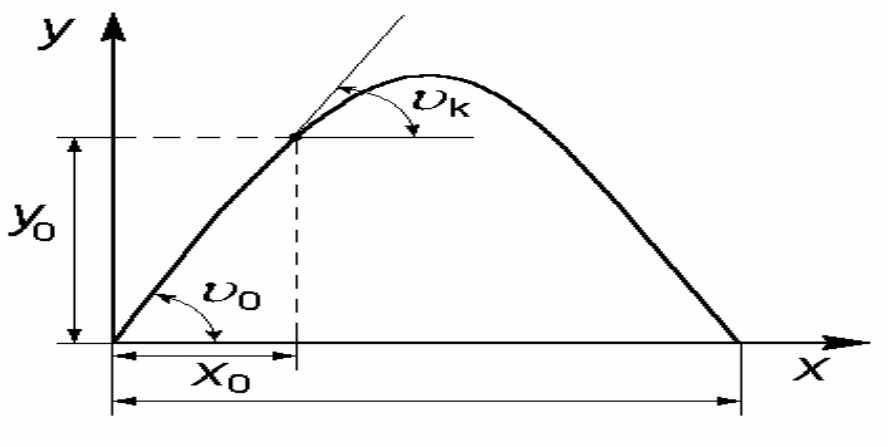
Рисунок 1.3 – Траектория полета ракеты

В точной постановке задача выбора оптимальной программы по тангажу (t) очень сложна и практически не имеет аналитического решения. Однако для целей баллистического проектирования можно ограничиться несколькими приближенными программами.

Например, для управляемой баллистической ракеты близкой к оптимальной является программа, описываемая соотношением

(1.1)

где угол старта ракеты;

значение угла тангажа в конце активного участка траектории;

текущее значение относительной массы ракеты, равное

.

Начальное значение угла тангажа следует выбирать в пределах

.

Значение соответствует вертикальному старту. Оптимальное значение угла тангажа в конце активного участка близко к . Если пренебречь высотой конца активного участка траектории по сравнению с радиусом Земли, то более точное значение можно определить из условия

, (1.2)

где коэффициент, показывающий во сколько раз полная (максимальная) дальность больше дальности пассивного участка траектории, т.е.

. (1.3)

З начение коэффициента зависит от дальности , причем, чем больше дальность полета, тем меньше значение . Для предварительных расчетов можно принять . При расчетах с использованием ЭВМ эту неопределенность с коэффициентом можно практически исключить.

С учетом изложенного алгоритм определения значения угла тангажа в конце активного участка траектории следующий: задавшись из рекомендуемого диапазона конкретным значением по формуле (1.2) найти значение , решить уравнение движения ракеты и получить соотношение полной дальности полета и дальности пассивного участка траектории, т.е. найти .

В соответствии с формулой (1.2) скорректировать значение угла и вновь провести интегрирование уравнений движения. При необходимости эту процедуру можно повторить, хотя уточнения при повторе будут незначительными.

Проведенные расчеты показывают, что для обеспечения доставки ракеты на максимальную дальность с учетом исходных данных необходимо обеспечить в конце активного участка траектории угол тангажа, равный .

Выбор топлива при проектировании имеет особое значение, т.к. природа топлива и его свойства практически полностью определяют тип двигателя, систему проектных параметров, массу, габариты и баллистические возможности ракеты. Следует также иметь в виду то, что в тактических и оперативно-тактических ракетах около 50 % стартовой массы приходится на долю топлива.

Наконец, структура, состав, надежность и боеготовность ракетного комплекса зависят от эксплуатационных свойств топлива. Выбор топлива производится по следующим основным показателям:

– величина удельного импульса и плотность ρ_Т;

– скорость горения u;

– чувствительность скорости горения к изменению давления в камере сгорания p_K и температуры заряда Т_з;

– физико-механические свойства.

Ч ем больше I_У и ρ_Т, тем меньше масса и габариты ракеты. Поэтому наивыгоднейшим является топливо с таким сочетанием I_У и ρ_Т, при котором достигается наибольшая величина идеальной скорости ракеты V_И, рассчитываемой по формуле К.Э. Циолковского

, (1.4)

где m₀, , стартовая масса, масса топлива и масса конструкции соответственно;

удельный импульс в пустоте.

Представим массу конструкции в виде суммы

, (1.5)

где m_КД – массса камеры двигателя, зависящая от объема, рассматриваемого в ней топлива, т.е.

. (1.6)

Тогда (1.4) преобразуется к виду

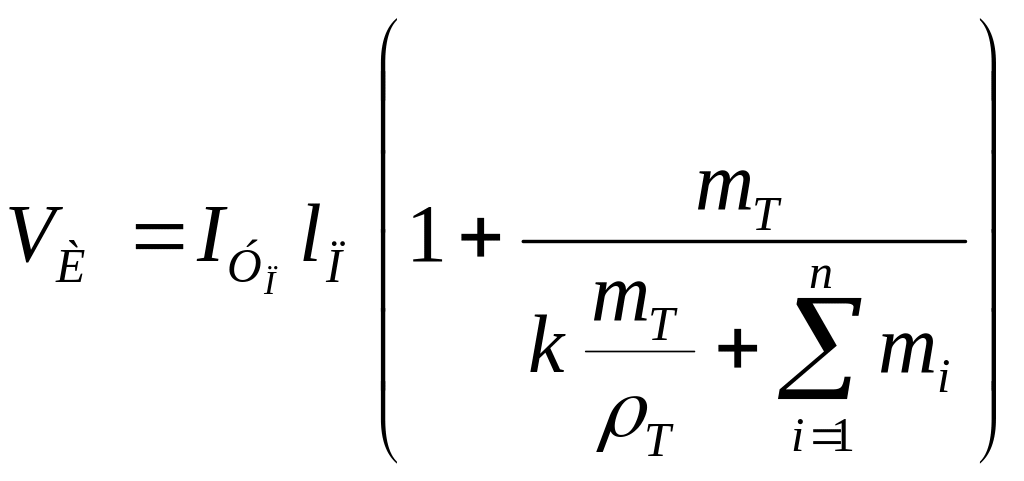. (1.7)

Откуда нетрудно видеть, что при одной и той же массе топлива m_T, лучшим признается топливо, у которого выше I_У и . Скорость горения топлива u предопределяет удлинение заряда , а оно, в свою очередь, – начальную тяговооруженность n₀.

Чувствительность скорости горения к изменению температуры заряда сгорания и температура заряда определяет разброс параметров двигателя – тяги и времени работы. Чем оно больше, тем больше разброс параметров. Поэтому желательно выбирать топливо с низкой чувствительностью.

Ч увствительность к изменению давления характеризуется величиной показателя в зоне горения

, (1.8)

а чувствительность к изменению температуры заряда – величиной термохимического коэффициента B. Значения этих величин приведены в таблице 1.2.

Топлива с низкой чувствительностью имеют малый показатель  и большой коэффициент B.

Основными физико-механическими характеристиками твердых топлив являются прочность, эластичность и температура стеклования. Прочность задается предельным напряжением , эластичность – предельным относительным удлинением . Для управляемых тактических и оперативно-тактических ракет прочность современных топлив, как правило, оказывается достаточным и может не учитываться при выборе топлива.

Таблица 1.2 – Значения характеристик смесевого твердого топлива СТ 15/18

Величина	Размерность	Значение	Название характеристики
	кг/м3	1767	плотность топлива
R	Дж/кг	308	газовая постоянная
	К	3294	температура горения топлива
п	–	1,13	показатель политропии
u1	мм/с	1,9	скорость горения топлива при нормальных условиях
	–	0,3	показатель чувствительности
В	С	440	термохимический коэффициент
	МПа	4	предельное напряжение сжатия
	МПа	0,7	предельное напряжение растяжения
Е	МПа	16	модуль упругости
	%	31	относительное удлинение
ТСТ	С	–70	температура стеклования
	Нс/кг	2445	удельный импульс

Эластичность топлива определяет выбор типа заряда – вкладной или скрепленный с корпусом двигателя. Для скрепленного заряда существует опасность растрескивания и отслоения от стенок корпуса при деформациях двигателя. По этой причине для изготовления скрепленных зарядов пригодны только эластичные топлива, имеющие предельное удлинение _пр и не менее 12...15 % менее эластичные топлива пригодны только для вкладных зарядов.

Температурой стеклования Т_СТ называется такая температура, при охлаждении до которой топливо теряет свою эластичность и переходит в хрупкое состояние. Эксплуатация ракет при температуре заряда ниже Т_СТ недопустима. Поэтому желательно выбирать топливо, температура стеклования, которого ниже –500 С.

В соответствии с этими требованиями выбираем твердое ракетное топливо СТ 15/18 со скрепленным типом заряда.

Как будет показано ниже, при принятой программе движения ракеты, параметры ее движения в любой момент времени, а, следовательно, и дальность полета, зависят от следующих факторов:

– относительной массы топлива

; (1.9)

– начальной тяговооружености двигателя

; (1.10)

– начальной нагрузки на миделево сечение

; (1.11)

– удельного импульса двигателя I_У.

И наче говоря, дальность полета ракеты можно представить в виде функции

.

Эту зависимость можно рассматривать как обратную функцию вида

.

Оказывается и стартовая масса ракеты m₀ при известном топливе, ККС, материалах конструкции может быть представлена в виде функции,

,

а имея в виду зависимость относительной массы топлива

.

Таким образом, если известны максимальная дальность полета L_max, масса полезной нагрузки m_ПН, то при выбранных программе полета, топливе, материалах конструкции и ККС, задача баллистического расчета (определение относительного потребного запаса топлива ) и проведение весового анализа (определение стартовой массы m₀ и масс составных частей m_i) могут быть решены, если известны I_У, n₀ и P_М.

Проектными параметрами ракеты называют совокупность исходных величин, задавшись которыми можно однозначно определить основные баллистические, весовые, тяговые и геометрические характеристики ракеты (при условии, что заданы L_max, m_ПН и выбраны тип топлива, конструкционные материалы, ККС и программа полета).

Проектные параметры должны удовлетворять ряду требований, а именно:

– должны однозначно определять характеристики ракеты;

– должны существенно влиять на основные характеристики ракеты;

– должны быть независимыми;

– должны иметь большой диапазон изменения и их рациональные значения можно достаточно предсказать.

Х отя в уравнениях движения и весовых уравнениях фигурируют в основном параметры I_У, n₀ и P_М, практическими параметрами для РДТТ следует считать:

– давление в камере p_K;

– давление на срезе сопла p_a;

– начальную тяговооруженность n₀;

– относительное удлинение заряда .

Удельный импульс, являющийся характеристикой энергетических возможностей топлива и организации рабочего процесса в камере ракетного двигателя, можно определить по формуле

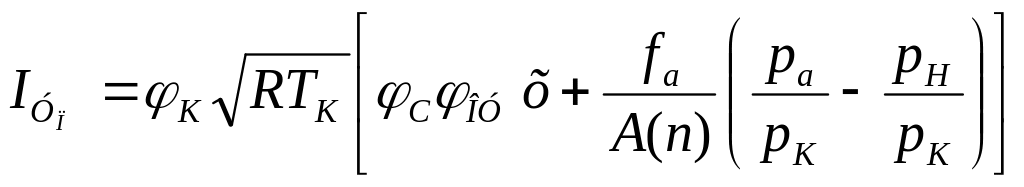; (1.12)

, (1.13)

где коэффициент потерь удельного импульса в камере сгорания;

коэффициенты потерь удельного импульса в сопле и на органах управления соответственно;

работоспособность продуктов сгорания топлива, зависящая от рода топлива;

степень расширения сопла, является функцией степени расширения газа и показателя процесса истечения n, т.е.

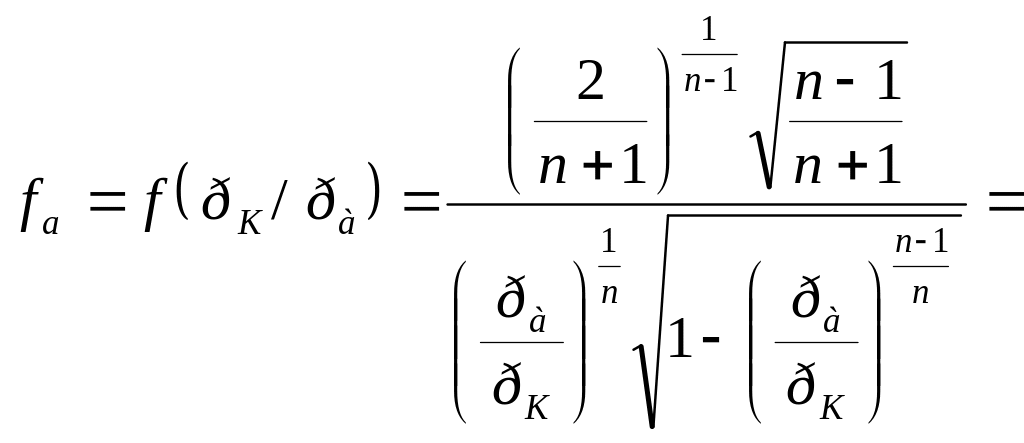
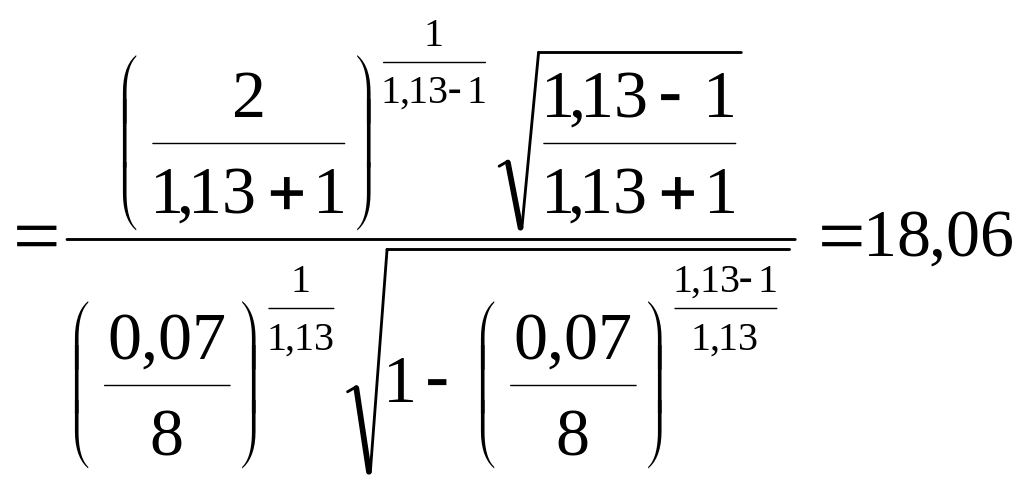. (1.14)

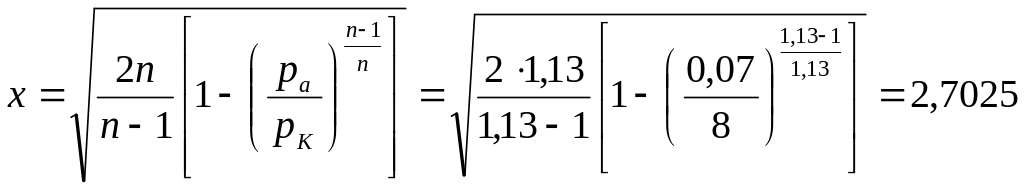; (1.15)

. (1.16)

Таким образом, для выбранного топлива величина удельного импульса будет определена как на земле ( МПа), так и в пустоте , если выбраны значения давления в камере p_K и на срезе сопла p_a.

От величины давлений в камере сгорания p_K и на срезе сопла p_a зависят удельный импульс I_У, размеры и масса двигателя, т.е. значения давлений p_K и p_a влияют на массу и на летные характеристики ракеты.

При повышении давления в камере сгорания непрерывно увеличивается удельный импульс РДТТ I_У. Но с повышением p_K растет и масса конструкции двигателя, т.к. потребная толщина несущей оболочки камеры сгорания прямо пропорциональна давлению в камере сгорания. В итоге давление p_K выгодно повышать лишь до определенных значений. Обоснованный выбор давления p_K требует прямых расчетов и последующего анализа параметров ракеты при различных значениях p_K.

Исследования показывают, что давление в камере сгорания, отвечающее минимуму стартовой массы ракеты при заданных L_max и m_ПН, зависит в основном от свойств топлива, конструкционных материалов для двигателя, относительной длины заряда и находится в пределах 5…10 МПа.

В ыбор давления на срезе сопла производится на основе следующих соображений. Понижение p₀ (до определенного предела) при неизменном p_K приводит к росту удельного импульса, но одновременно требует увеличения длины сопла, а стало быть, массы сопла и массы основного отсека. Суммарное влияние давления p_a таково, что существует вполне определенное значение давления, при котором для обеспечения заданной дальности полета L_max требуется ракета наименьшей массы. Оптимальные значения p_a лежат обычно в пределах 0,05…0,09 МПа. Причем чем больше дальность пуска, тем меньше оптимальное значение p_a, а меньшему значению p_a соответствует и меньшее наивыгодное значение давления в камере сгорания p_K.

При строгом подходе к решению задачи баллистического проектирования описание наивыгоднейших значений p_a и p_K должно осуществляться совместно. Само решение задачи тогда должно сводиться к прямому расчету стартовой массы m₀ при различных сочетаниях p_K и p_a, построению графиков и выбору такой комбинации p_K и p_a, при которой m₀ = min, т.е. должна решаться задача оптимизации параметров p_K, p_a по критерию минимума стартовой массы ракеты m₀.

Начальная тяговооруженность двигателя n₀ предопределяет величину ускорения ракеты, а стало быть, набора скорости, что приводит к изменению гравитационных и аэродинамических потерь скорости и изменению величины нагрузок, действующих на корпус ракеты. С увеличением n₀ интегральные гравитационные потери уменьшаются (ракета быстро удаляется от центра притяжения), суммарные аэродинамические потери возрастают (ракета плотные слои атмосферы проходит с большой скоростью), нагрузки на корпус ракеты также возрастают.

Изменение потерь скорости приводит к изменению потребного запаса топлива , изменению нагрузок на корпус ракеты предопределяет изменение толщины стенок корпуса, а все вместе взятое влияет на величину стартовой массы ракеты m₀.

Отыскание оптимального значения n₀ должно сводиться к прямому расчету стартовой массы m₀ при различных значениях n₀ и выбору из этой совокупности того значения, при котором стартовая масса имеет минимальное значение.

Из опыта создания ракет можно рекомендовать следующие значения:

– для управляемых ракет с вертикальным стартом;

– для управляемых ракет с наклонным стартом.

Относительное удлинение заряда во многом предопределяет тяговооруженность ракеты. Действительно, тяга двигателя равна

,

где площадь горящей поверхности, зависящая как от формы заряда, так и его длины l_з.

Оказывается, что ракета с двигателем твердого топлива может обладать хорошими характеристиками только при определенном сочетании свойств топлива, формы заряда и его относительной длины.

Плотность твердых топлив колеблется в пределах от 1700 до 2000 кг/м³. Выбор формы заряда также ограничен. Поэтому большое значение имеет подбор топлив с приемлемой скоростью горения u и выбор относительной длины заряда .

Расчеты показывают, что рациональное значение лежит обычно в пределах 3…5. Задача состоит в подборе такого сочетания формы заряда и скорости горения, которое обеспечило бы близкое к оптимальному удлинение заряда. Для решения данной задачи получим уравнение, связывающее эти параметры.

По определению, нагрузка на миделево сечение

. (1.17)

Тяга двигателя у Земли

, (1.18)

где площадь горящей поверхности, рассчитываемая по выражению

.

Коэффициент формы заряда k_Ф представляет собой отношение площади горящей поверхности канального заряда к длине канального заряда, а диаметр внутреннего канала.

При проектировании канально-щелевого, звездообразного заряда можно принять k_Ф =1,8…3,0. Тогда нагрузка на миделево сечение запишется

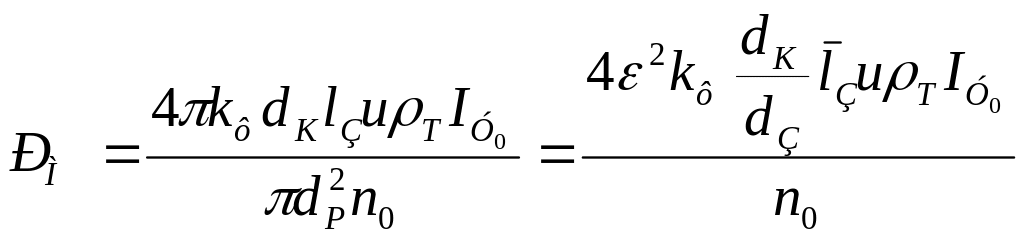. (1.19)

Здесь показывает соотношение диаметров заряда и ракеты. При проектировании можно принять, что для скрепленного заряда и для вкладного заряда.

Имея в виду условие прочности заряда , отношение

.

Тогда окончательно можно записать

Па.

Порядок предварительного выбора значений проектных параметров следующий:

1. Выбираются значения p_K и p_a.

В работе принимаем p_K = 8 МПа, а p_a =0,07 МПа.

2. Для выбранного типа топлива и значений p_K, p_a рассчитываются удельный импульс на Земле и в пустоте по выражениям (1.12) (1.13) соответственно:

; * .

3. Рассчитывается скорость горения топлива u, соответствующая выбранному давлению в камере сгорания p_K

м/с,

где подставляется в МПа;

u₁,  – некоторые константы для данного топлива (таблица 1.2).

4. Выбирается значение начальной тяговооруженности n₀, исходя из типа проектируемой ракеты (n₀ принимаем равным 4).

5 . Из области рациональных значений 3…5 выбирается относительное удлинение заряда . Большему значению тяговооруженности соответствует большее значение . Допускается относительная длина заряда до 7 единиц.

6. По формуле (1.17) рассчитывается нагрузка на миделево сечение. Если P_M оказывается в пределах (0,6…1,2)10⁵ Па для управляемой ракеты, то предварительный выбор проектных параметров можно считать удавшимся. В противном случае следует пересмотреть значения проектных параметров.

Кроме параметров p_K, p_a, n₀, , P_M в уравнениях движения и в весовых уравнениях будем использовать и другие параметры. В частности:

– идеальное время работы двигателя

c;

– текущее значение относительной массы ракеты

,

причем относительная масса ракеты в конце активного участка траектории, равная (с учетом времени работы двигателя )

.

При пуске на максимальную дальность в конце активного участка траектории топливо должно все выгореть, поэтому относительный запас топлива

,

где коэффициент, учитывающий достартовый и гарантийный запасы топлива.

О дна и та же дальность полета может обеспечиваться при различных сочетаниях проектных параметров p_K, p_a, n₀, . Но изменение сочетания проектных параметров влечет изменение стартовой массы и размеров ракеты. Задачу по отысканию сочетания проектных параметров, обеспечивающих наиболее приемлемый вариант ракеты, называют задачей оптимизации проектных параметров. Она может быть сформулирована следующим образом.

Определить значения проектных параметров p_K, p_a, n₀, , которые при выбранных конструктивно-компоновочной схеме ракеты, типе топлива, конструкционных материалах, законе управления, а также заданных L_max и m_ПН обеспечивают наименьшее значение стартовой массы ракеты m₀.

В принципиальном плане данная постановка задачи не вызывает особых трудностей ее решения. Трудности обусловлены огромным объемом вычислений, которые немыслимы без использования ЭВМ.

Выводы

В первом разделе приведена классификация управляемых баллистических ракет и требования предъявляемые к ним. Управляемые баллистические ракеты классифицируются по ряду признаков: по месту старта и цели; по боевому назначению; по типу двигателя; по типу СУ; по числу ступеней и способам их соединения.

Т актико-технические требования основываются на анализе боевого применения проектируемой ракеты и должны учитывать накопленный опыт создания аналогичных ракет, а также технические возможности. Конечной целью разработки ракеты является достижение максимальной эффективности ее действия как боевого средства, удобства эксплуатации и технологичности изготовления. Кроме того, все предъявляемые требования должны обеспечить безотказный пуск ракеты в заданное время и ее полет по заранее рассчитанной программе. Особый акцент делается на производственно-экономические требования. Тактико-технические требования, предъявляемые к проектируемой ракете значительно выше, чем требования, предъявляемые к предыдущим ракетам того же класса. Заказчику нужна ракета, имеющая небольшие габариты и массу с высокой точностью попадания. Ракета должна использоваться в различных климатических условиях, и в любой местности.

Кроме того, в первом разделе дипломной работы проведен выбор и обоснование схемы ракеты.

Схема ракеты: тип двигателя – РДТТ; тип старта – наклонный; тип топлива – СТ15/18.

Конструктивно-компоновочная схема: головная часть, приборный отсек, двигательная установка; хвостовой отсек, а также:

– выбрана программа полета, соответствующая наклонному старту и дальности пуска 310 км;

– конструкционные материалы;

– выбраны проектные параметры , , P_M, Т и n₀;

– выведено уравнение движения ракеты;

– дана методика определения относительного запаса топлива.

2 Расчет стартовой массы и геометрических размеров ракеты

Прежде чем приступить непосредственно к расчету стартовой массы и геометрических размеров, необходимо провести баллистический расчет. Основной целью баллистического расчета является определение относительного потребного минимального запаса топлива , обеспечивающего достижения требуемой дальности L_max. Решение данной задачи основывается на анализе уравнений движения ракеты, которые в зависимости от принятых допущений могут иметь различную степень сложности.

2.1 Уравнения движения ракеты

П ри проектировании рассматривают упрощенные уравнения движения центра масс ракеты относительно стартовой системы координат, связанных с Землей, которую считают неподвижной. Будем пренебрегать боковым движением и влиянием вращательного движения ракеты на дальность. Кроме того, для управляемой ракеты будем считать СУ идеальной, т.е. в каждый момент времени угол тангажа  равен своему программному значению.

Для вывода уравнений движения на активном участке траектории рассмотрим схему сил, действующих на ракету (рисунок 2.1). Движение будем рассматривать в центральном поле тяготения относительно осей прямоугольной стартовой системы координат, начало которой совпадает с точкой старта.

При принятых допущениях уравнения движения примут вид:

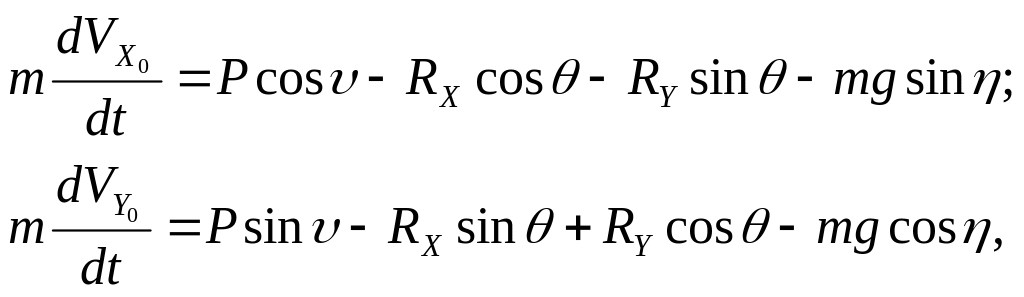(2.1)

где m – текущие значение массы ракеты;

P – сила тяги двигателя;

R_X, R_Y – сила лобового сопротивления и подъемная сила;

 – угол тангажа;

θ – угол наклона вектора скорости к плоскости стартового горизонта;

 – полярный угол;

g – ускорение свободного падения.

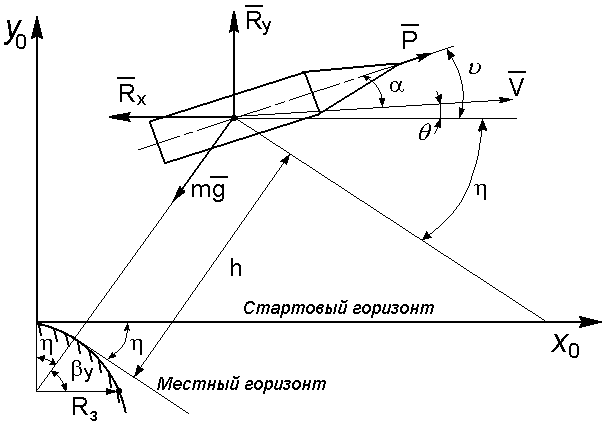
Рисунок 2.1 – Траектория движения ракеты

Поскольку при решении прямой задачи баллистического проектирования характеристики ракеты неизвестны, то преобразуем уравнения движения так, чтобы они были записаны через проектные параметры.

Относительная масса ракеты

,

где идеальное время.

Тогда текущее значение массы рассчитывается по формуле

.

Сила тяги ракетного двигателя равна

,

где , сила тяги в пустоте и на Земле соответственно;

, давление воздуха на данной высоте и на поверхности Земли соответственно.

Считаем, что атмосферное давление меняется с высотой согласно принятой модели атмосферы.

Учитывая, что

,

найдем

,

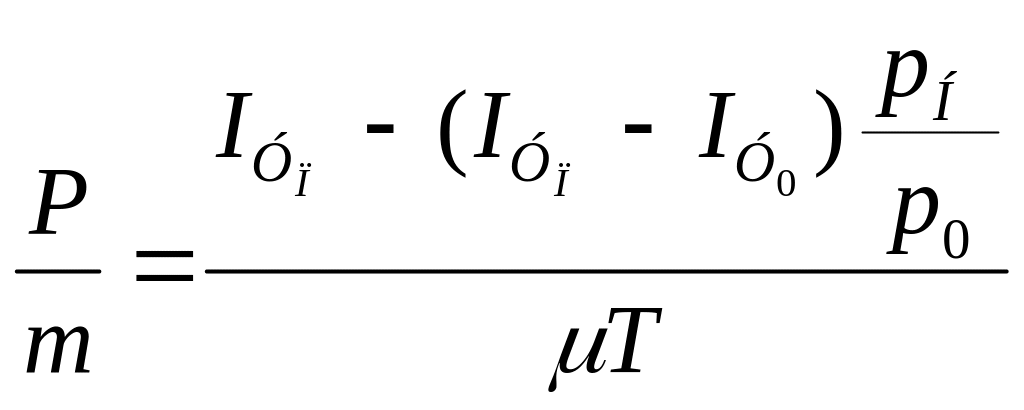где , значения удельного импульса в пустоте и на Земле, являющегося характеристикой топлива и выбранных значений давления в камере сгорания и на срезе сопла.

Известно, что сила лобового сопротивления определяется по формуле

.

Тогда

.

По аналогии можно записать, что

.

Пользуясь понятием коэффициента перегрузки ( ), уравнения движения (2.1) ракеты можно записать в виде

(2.2)

где

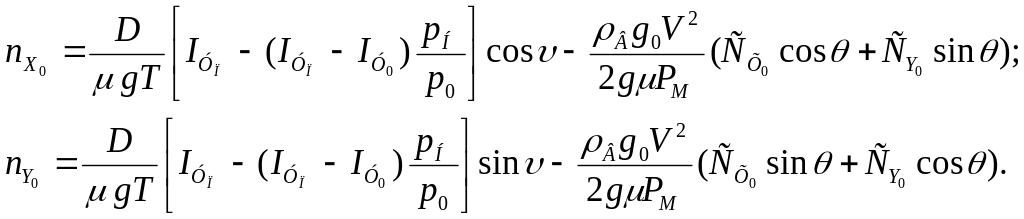(2.3)

С истема дифференциальных уравнений (2.2) оказывается оправданной как для активного, так и для пассивного участков траектории. Необходимо лишь иметь ввиду, что на активном участке траектории , а на пассивном . Кроме того, относительная масса ракеты на пассивном участке траектории неизменна, т.е. .

Для целей расчета корпуса ракеты на прочность нужны значения коэффициентов перегрузки по осям связанной системы координат

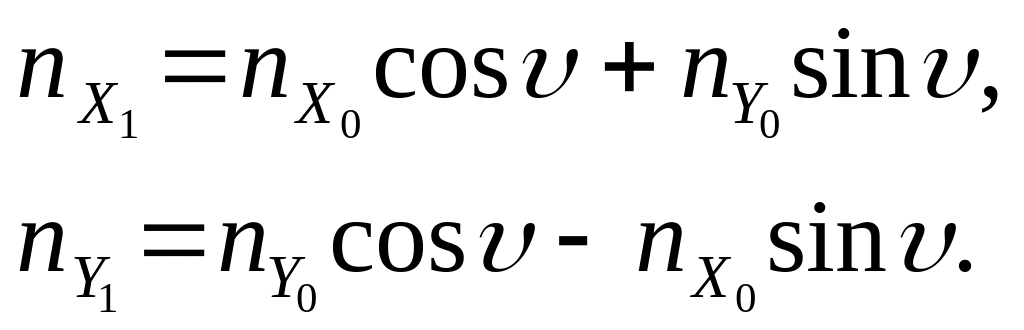(2.4)

Для определения правых частей дифференциальных уравнений в соответствии с рисунком 2.1 имеем

; ; ;

; ;

В начальный момент времени, т.е. в точке старта ракеты, когда естественно необходимо принять , где начальный угол тангажа (угол старта ракеты).

Коэффициенты аэродинамической силы С_X и C_Y можно рассматривать по приближенным зависимостям

(2.5)

где

(2.6)

(2.7)

(2.8)

; . (2.9)