Тема 4. Экономико-математические методы в анализе

Вопросы для обсуждения:

1. В чём отличие стохастических связей от функциональных?

2. Почему стохастический анализ имеет вспомогательный характер?

3. Каковы задачи корреляционного и регрессионного анализа?

4. Изложите порядок расчёта и использование коэффициента детерминации.

5. Для каких целей и каким образом используются результаты корреляционного анализа?

6. Как проводится многофакторный корреляционный анализ?

7. Раскройте параметры однофакторной линейной регрессии (уравнение прямой).

8. Как методы регрессии применяются для получения простых прогнозов?

9. Охарактеризуйте составные элементы временных рядов и их интерпретацию.

10. Раскройте содержание и область применения математических методов анализа.

11. На чём основывается логика имитационного моделирования?

12. Где нашли практическое применение методы линейного программирования?

13. В чём смысл математической теории игр?

14. Раскройте суть анализа чувствительности?

Задача 1. Приведены данные, характеризующие реализацию продукции и производительность труда торгового предприятия

№ предприятия	выполнение плана реализации продукции, %	производительность труда, тыс. руб.
1	103,5	5,34
2	97,6	5,22
3	101,1	5,44
4	84,6	4,42
5	103	5,5
6	100,2	4,99
7	90,5	4,55
8	102,8	5,49
9	99,3	5,29
10	100,1	5,31
11	104	5,72
12	100,8	5

1. построить уравнение регрессии, считая форму связи этих показателей линейной;

2. измерьте тесноту корреляционной связи между производительностью труда и выполнением плана реализации;

3. выполнить проверку правильности построения уравнения регрессии;

4. проанализировать рассчитанные показатели;

Решение:

1. Построим расчетную таблицу:

x	y	xy	x2	y2	yx	/y- yx/	(y- yx)2	ε, %
5,34	103,5
5,22	97,6
5,44	101,1
4,42	84,6
5,5	103
4,99	100,2
4,55	90,5
5,49	102,8
5,29	99,3
5,31	100,1
5,72	104
5	100,8
62,27	1187,5

,

=

=

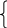
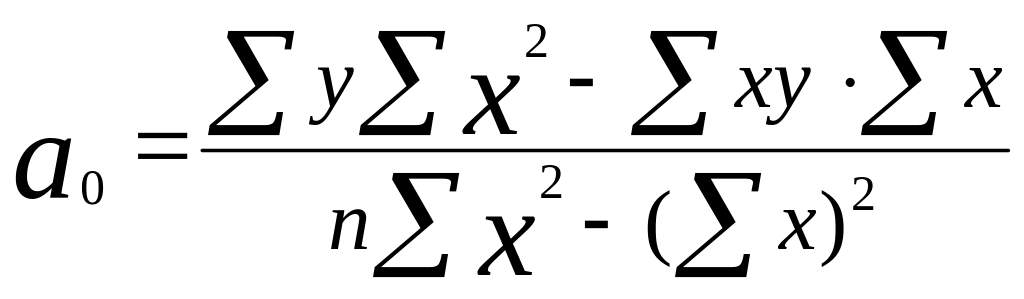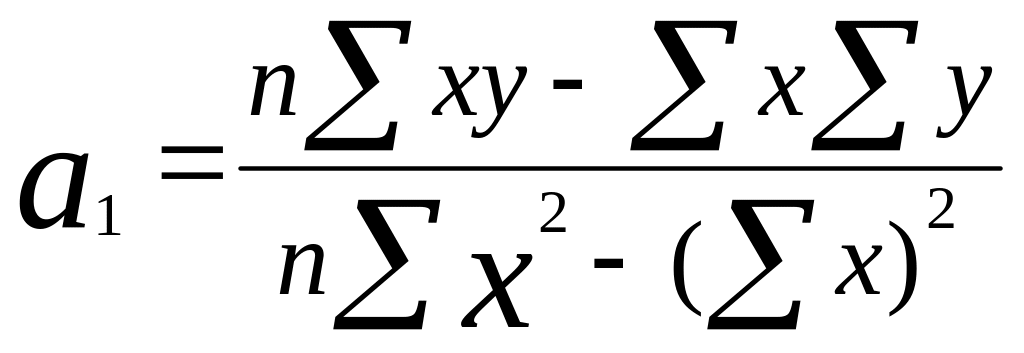В нашем уравнении регрессии параметр a₁=______показывает, что

Таким образом, уравнение регрессии по данному примеру примет вид: =_____+_______x

Средний коэффициент эластичности определим по формуле:

=

Коэффициент эластичности, равный _____ показывает, что

Измерим тесноту корреляционной связи между производительностью труда и выполнением плана реализации линейным коэффициентом парной корреляции, теоретическим корреляционным отношением, индексом корреляции:

=

=

= =

= = =

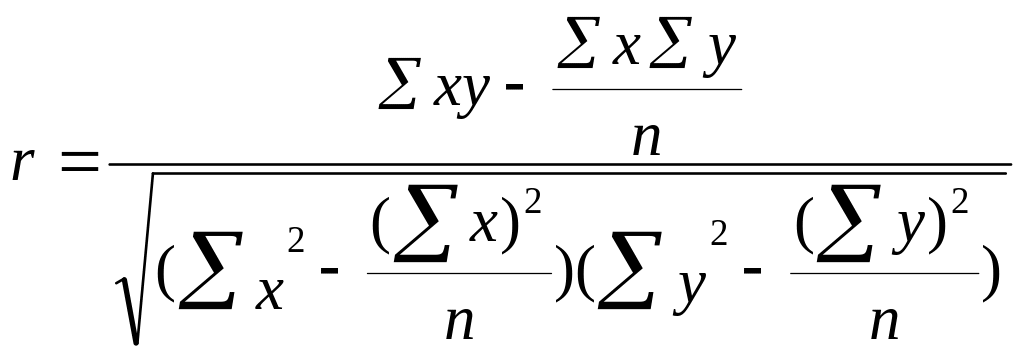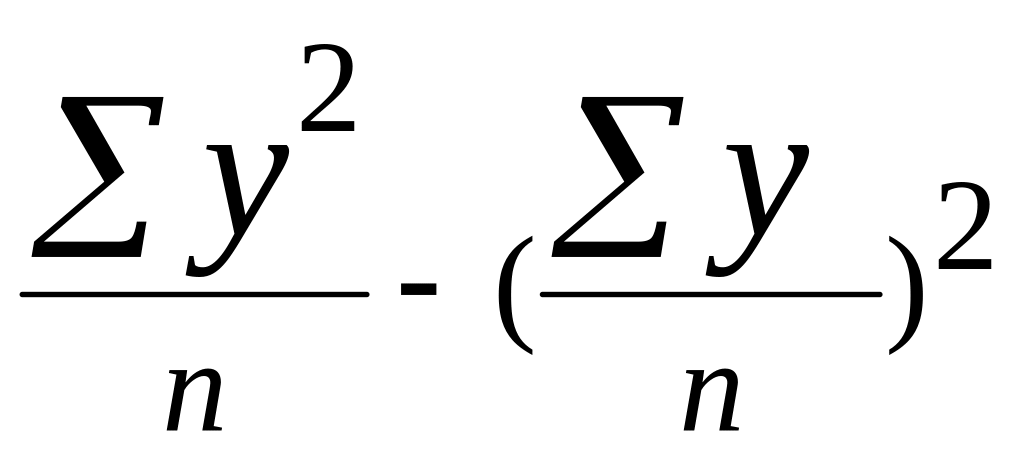Коэффициент детерминации η² равен ____. Это означает, что вариация выполнения плана реализации на _____% объясняется вариацией производительности труда и на _____ % - прочими факторами. Индекс корреляции определим по формуле:

=

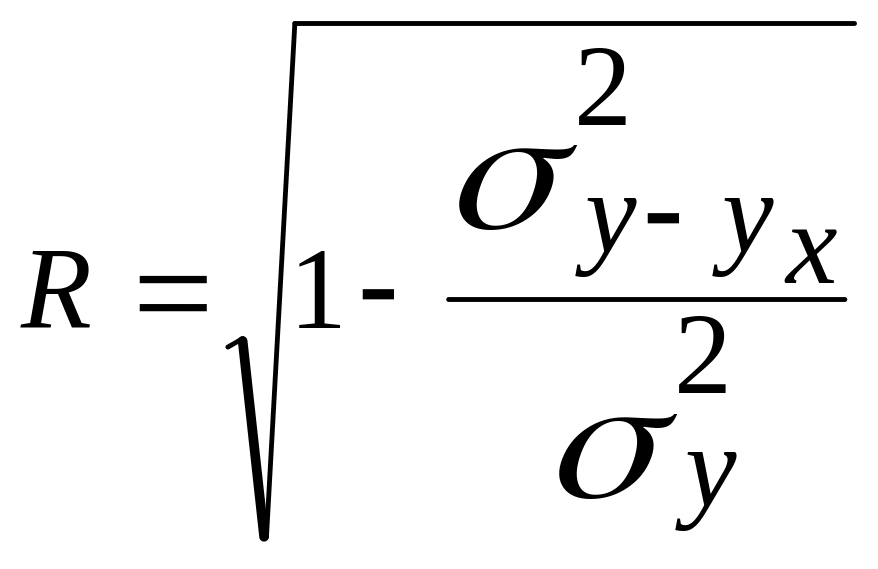Все показатели тесноты корреляционной связи показывают тесную связь между производительностью труда и выполнением плана реализации.

Так как, r=R=η, то можно сделать заключение, что гипотеза о линейной форме связи подтверждена.

Проведем оценку адекватности регрессионной модели

=______+_______x,

выражающей зависимость между производительностью труда и выполнением плана реализации, с помощью F-критерия Фишера:

=

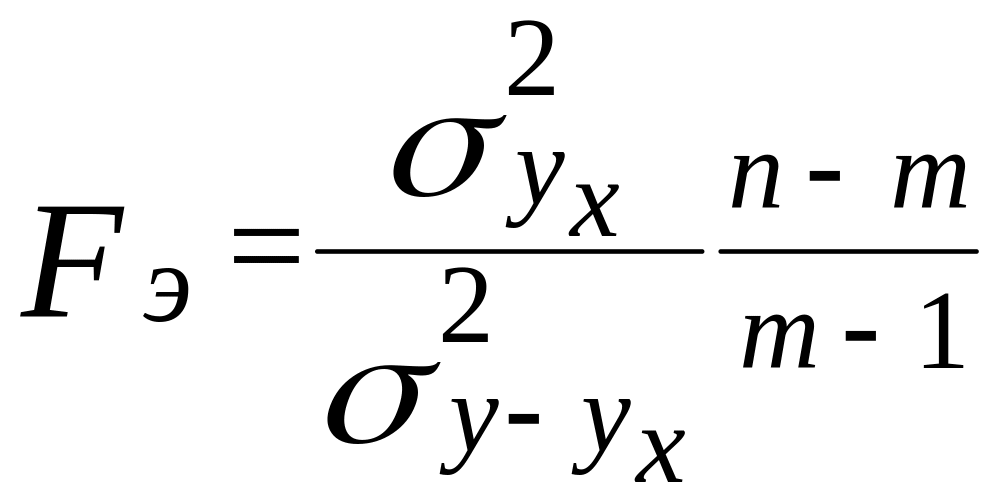Эмпирическое значение F больше табличного, следовательно, уравнение регрессии можно признать адекватным.

Оценим значимость параметров уравнения регрессии с помощью t-критерия Стьюдента:

=

=

=

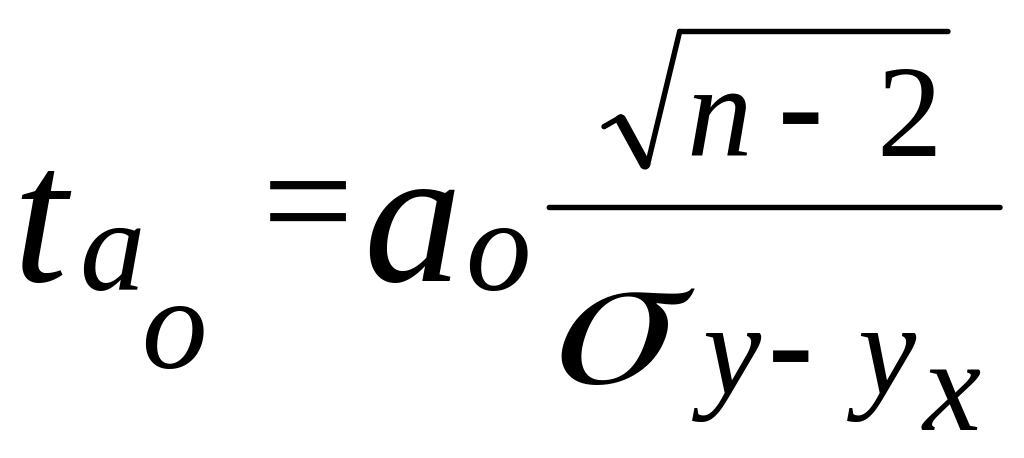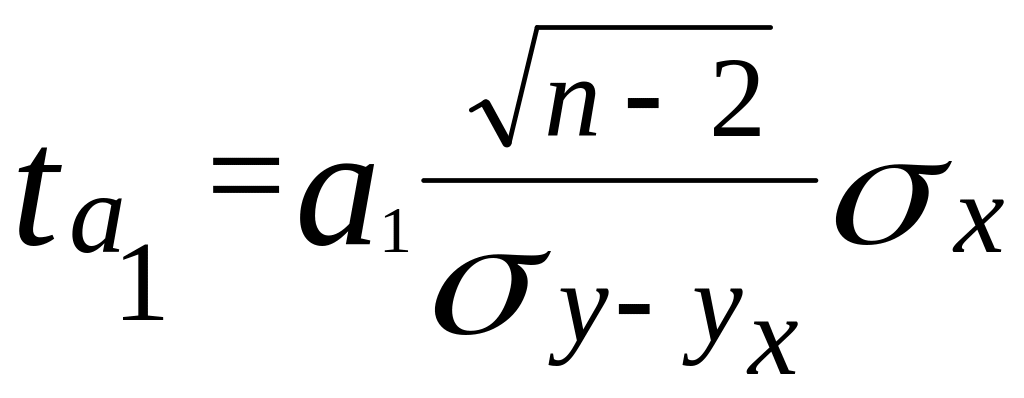Табличное значение t-критерия с уровнем значимости 0,05 и числом степеней свободы (n-2) равно 2,307. Так как, t_эмп>t_табл,, то параметры Уравнения регрессии признаются значимыми.

Значимость коэффициента корреляции оценим с помощью t- критерия Стьюдента по формуле:

=

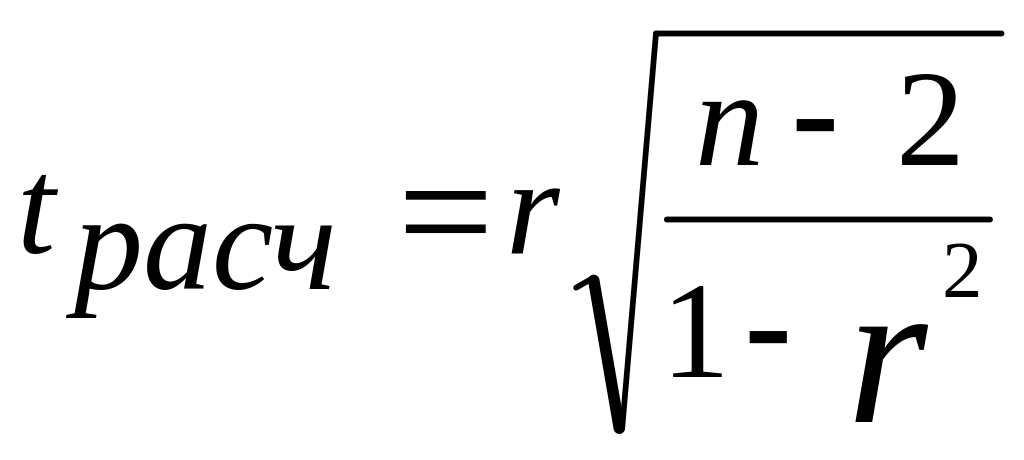Эмпирическое значение t больше табличного, следовательно, коэффициента корреляции можно признать значимым.

Вычислим ошибку аппроксимации по формуле:

=

На основании данных расчетов можно сделать заключение, что построенная регрессионная модель зависимости производительности труда от выполнения плана реализации может быть использована для анализа и прогноза.