
Уравнение Шредингера (общие свойства).
A) Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение... B) Нестационарным уравнением Шредингера для частицы в потенциальном поле является уравнение... C) Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение ... |
|
||||
Задана пси-функция
|
|
||||
Стационарное уравнение Шредингера
имеет вид
|
|
||||
Стационарное уравнение Шредингера в
общем случае имеет вид
|
|
||||
Стационарное уравнение Шредингера в общем случае имеет вид . Здесь потенциальная энергия микрочастицы. Движение частицы вдоль оси ОХ под действием квазиупругой силы описывает уравнение …
|
|
||||
Нестационарным уравнением Шредингера является уравнение …
|
|
||||
Стационарное уравнение Шредингера в
общем случае имеет вид
.
Здесь
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
Уравнение Шредингера (конкретные ситуации).
Вероятность обнаружить
электрон на участке (а,b)
одномерного потенциального ящика с
бесконечно высокими стенками вычисляется
по формуле W
=
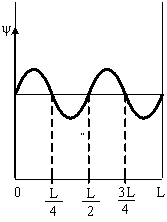
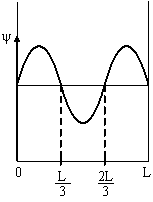
A) Если ψ -функция имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке L/6 <х< 5L/6 равна... B) Если ψ -функция имеет вид. указанный на рисунке, то вероятность обнаружить электрон на участке L/6 <х< L равна... C) Если ψ-функция имеет вид. указанный на рисунке, то вероятность обнаружить электрон на участке 3/8L < x <L, равна … |
2/3 5/6 1/3 1/2 3/8 5/8 1/4 |
||||
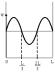
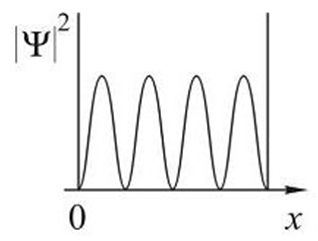
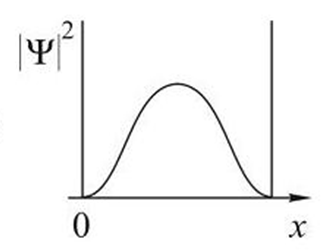
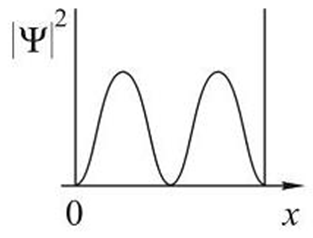
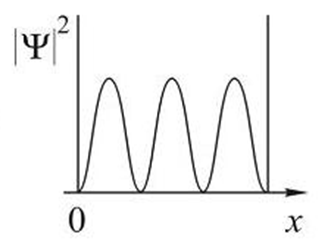
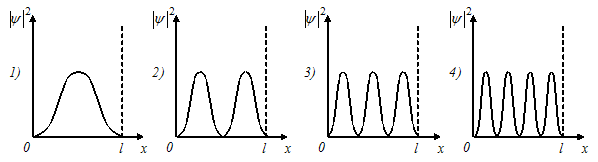
На рисунках приведены картины распределения плотности вероятности нахождения микрочастицы в потенциальной яме с бесконечно высокими стенками. Состоянию с квантовым числом п=1 соответствует ... Состоянию с квантовым числом п=2 соответствует ... Состоянию с квантовым числом п=3 соответствует ... Состоянию с квантовым числом п=4 соответствует ... |
|
||||
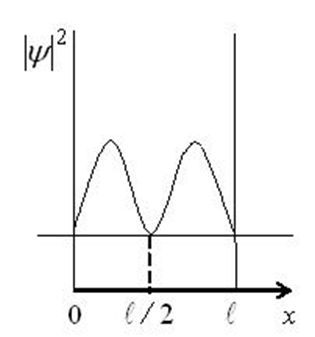
На рисунке изображена плотность вероятности обнаружения микрочастицы на различных расстояниях от «стенок» ямы. Вероятность ее обнаружения на участке l/4 < х < 3l/4 равна ...
|
0 1/4 1/2 3/4
|
||||
Электрон находится в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками в
состоянии с квантовым числом n =
4. Если
|
|
||||
Электрон находится в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками в
состоянии с квантовым числом n =
3. Если
-функция
электрона в этом состоянии имеет вид,
указанный на рисунке,
|
|
||||
|
|
||||
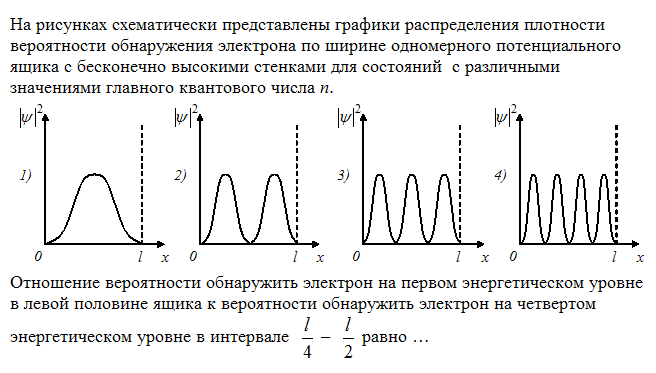
На рисунках схематически представлены
графики распределения плотности
вероятности обнаружения электрона
по ширине одномерного потенциального
ящика с бесконечно высокими стенками
для состояний с различными значениями
главного квантового числа n.
|
|
||||
|
|
||||
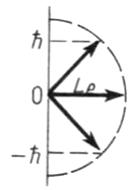
Момент импульса электрона в атоме и
его пространственные ориентации могут
быть условно изображены векторной
схемой, на которой длина вектора
пропорциональна модулю орбитального
момента импульса
|
|
||||
Момент импульса электрона в атоме и
его пространственные ориентации могут
быть условно изображены векторной
схемой, на которой длина вектора
пропорциональна модулю орбитального
момента импульса
электрона.
На рисунке приведены возможные
ориентации вектора
.
|
|
||||
|
|
||||
|
|
||||
|
|



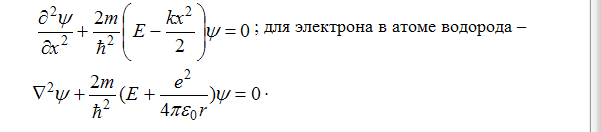






 то
вероятность обнаружить электрон в
интервале от
то
вероятность обнаружить электрон в
интервале от


 В
состоянии с n = 4 вероятность
обнаружить электрон в интервале от
В
состоянии с n = 4 вероятность
обнаружить электрон в интервале от
 Величина
орбитального момента импульса (в
единицах
Величина
орбитального момента импульса (в
единицах
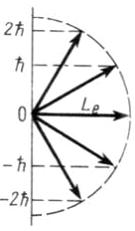 Значение
орбитального квантового числа для
указанного состояния равно …
Значение
орбитального квантового числа для
указанного состояния равно …




