Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

«Финансовый университет при Правительстве Российской Федерации»

Тульский филиал Финуниверситета

__________________________________________________________________

Кафедра математики и информатики

Пример выполнения контрольной работы по дисциплине

«Методы оптимальных решений»

(для бакалавров экономики)

Составил: к.ф.-м.н., доцент

кафедры математики и информатики

Луценко Алексей Георгиевич

Рассмотрено и одобрено на заседании кафедры

кафедры математики и информатики

протокол № ___ от «___»____________ 2013 г.

Задание 1

Изложить теоретический материал по вопросу Вашего варианта. Проиллюстрировать теоретические положения числовыми примерами.

Задача 1. Симплексный метод решения ЗЛП.

Примечание.

Задание 2

Решить графическим методом типовую задачу оптимизации. Осуществить проверку правильности решения с помощью средств MS Excel (надстройки Поиск решения).

С графическим методом решения ЗЛП и примерами решения подобных задач можно ознакомиться в литературе /1, стр. 53-60/, технологией оптимизации в среде MS Excel – в /2, стр. 28-48/. Кроме того, полезно дополнительно привлечь литературу /3,4,11/.

Пример 2.2.1 [3, с. 69-71]. Планирование выпуска продукции пошивочного предприятия (задача о костюмах).

Намечается выпуск двух видов костюмов – мужских и женских. На женский костюм требуется 1 м шерсти, 2 м лавсана и 1 человеко-день трудозатрат. На мужской костюм – 3,5 м шерсти, 0,5 м лавсана и 1 человеко-день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 человеко-дней трудозатрат.

Требуется определить, сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, а от мужского – 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

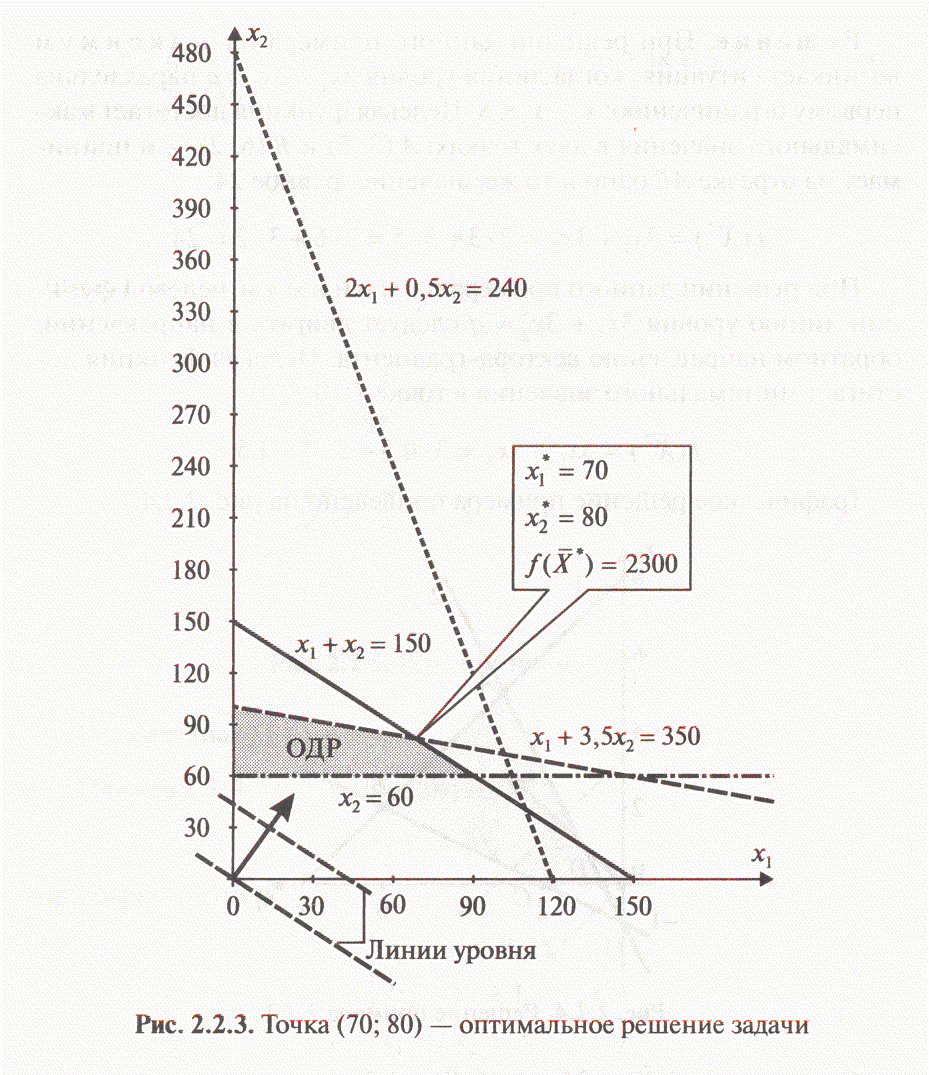
Приведем также решение этой задачи с помощью надстройки MS Excel Поиск решения (рис.1).

Рис. 1. Решение задачи о костюмах с помощью надстройки Поиск решения

Опишем кратко шаги решения задачи.

Вводим исходные данные:

в ячейки A4:B4 – коэффициенты целевой функции;

в ячейки A6:B6 – коэффициенты левой части ограничения по шерсти;

в ячейки A7:B7 – коэффициенты левой части ограничения по лавсану;

в ячейки A8:B8 – коэффициенты левой части ограничения по труду;

в ячейки E6:E9 – правые части ограничений.

Вводим зависимость для целевой функции:

в ячейку C4 вводим формулу =СУММПРОИЗВ(A4:B4;A3:B3).

Функцию СУММПРОИЗВ (массив1;массив2;массив;…) можно ввести с клавиатуры или вызвать с помощью Мастера функций, вызвав категорию Математические.

Вводим зависимости для ограничений:

в ячейку C4 вводим формулу =СУММПРОИЗВ(A6:B6;A$3:B$3).

Копируем эту формулу в ячейки C7:C9.

Вызываем надстройку командой меню Сервис – Поиск решения:

устанавливаем целевую ячейку, отмечаем «максимальному значению», заполняем поле Изменяя значения и поле Ограничения. Даем команду Выполнить.

Примечание. Более подробно технология решения этой задачи описана в учебном пособии [3, с. 95-105] и практическом пособии [4, с. 18-27].

Задание 3

Рассчитать параметры моделей экономически выгодных размеров заказываемых партий.

С необходимым теоретическим материалом и примерами решения подобных задач можно ознакомиться в литературе /1,стр.295-300; 2,стр.127-132/.

Пример 3.6 [2, с. 131-132]. Магазин «Лада» закупает духи «Ландыш» на одной из парфюмерных фабрик. Годовой спрос на этот продукт составляет 600 шт. Издержки заказа равны 850 руб., издержки хранения – 510 руб. за одну упаковку (20 шт.) в год. Магазин заключил договор на поставку с фиксированным интервалом времени.

Количество рабочих дней в году – 300. Время поставки товара 6 дней. Стоимость одного флакона 135 руб.

Требуется определить оптимальное число заказов в течение года, точку восстановления запаса, минимальные совокупные издержки.

Решение

Проведем необходимые вычисления в Excel по формулам модели наиболее экономичного размера партии (модель Уилсона, рис.1).

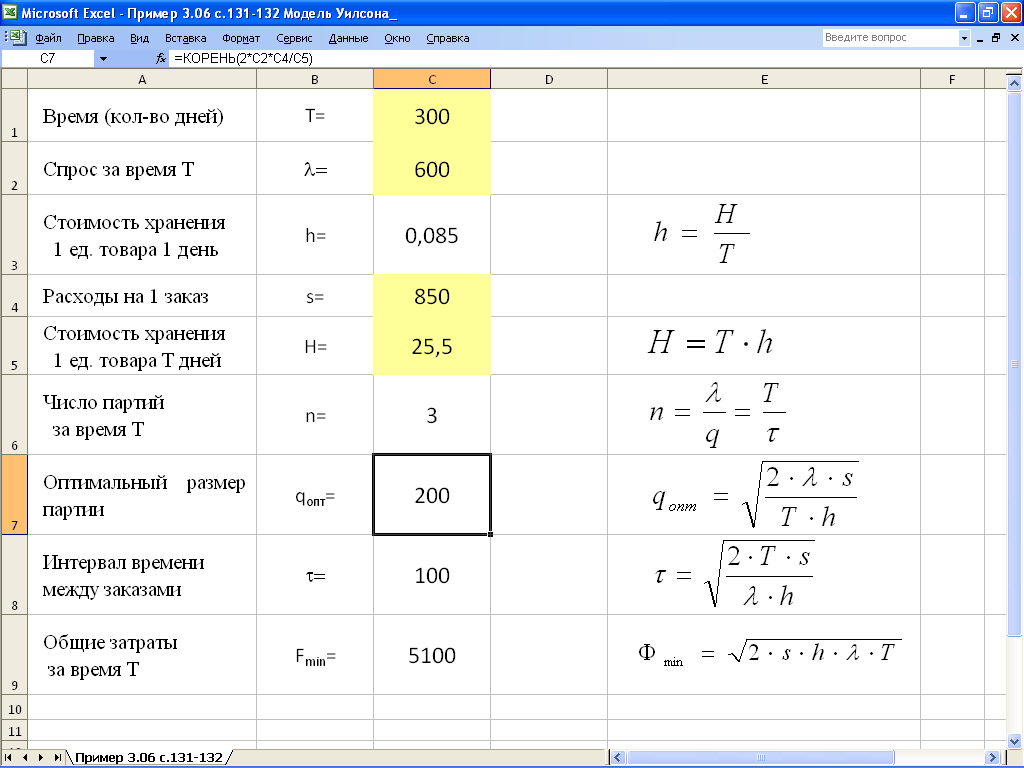
Рис. 1. Вычисления по формулам Уилсона

Вводим исходные данные в ячейки C1 (T = 300), C2 ( = 600), C4 (s = 850) и C5 (H = Th = 510/20 = 25,5).

Вычисляем оптимальный размер партии по формуле:

(в ячейку C7 вводим =КОРЕНЬ(2*C2*C4/C5)).

Функцию КОРЕНЬ (число) можно ввести с клавиатуры или вызвать с помощью Мастера функций, вызвав категорию Математические.

Число партий (заказов) в течение года вычисляем по формуле:

(в ячейку C6 вводим =C2/C7).

Интервал времени между заказами в течение года вычисляем по формуле:

(в ячейку C8 вводим =C1/C6) или

(в ячейку C8 вводим =КОРЕНЬ(2*C1*C4/(C2*C3))).

Определяем среднесуточный спрос по формуле:

(шт./день).

Точку восстановления запаса (уровень запасов, при которых делается новый заказ) вычисляем по формуле:

2(шт./день)6(дней) = 12 (шт.).

Минимальные совокупные издержки заказа и хранения вычисляем по формуле:

(в ячейку C9 вводим =КОРЕНЬ(2*C4*C3*C2*C1)).

Ответ. 1. Для минимизации расходов на оформление заказа, доставку и хранение товара необходимо: в течение года сделать три заказа; в каждом заказе поставить 200 шт. духов «Ландыш», т.е. 10 упаковок по 20 шт.; новый заказ делать при уровне запаса в 12 шт. духов «Ландыш». В этом случае совокупные издержки заказа и хранения в течение года составят 5100 рублей.

Задание 4

Использовать методы теории массового обслуживания для исследования предлагаемой хозяйственной ситуации. При моделировании предполагается, что поток требований на обслуживание является простейшим (пуассоновским), а продолжительность обслуживания распределена по экспоненциальному (показательному) закону. Задачу следует решить с помощью средств MS Excel.

Пример 3.1 [2, с. 108-109]. На строительном участке в инструментальной мастерской работают два мастера. Если рабочий заходит в мастерскую, когда оба мастера заняты обслуживанием ранее обратившихся работников, то он уходит из мастерской, не ожидая обслуживания. Статистика показала, что среднее число рабочих, обращающихся в мастерскую в течение часа, равно  = 18; среднее время, которое затрачивает мастер на заточку или ремонт инструмента, равно Т_ср = 10 мин.

Оценить основные характеристики работы мастерской как СМО с отказами. Сколько мастеров должно работать в мастерской, чтобы вероятность обслуживания рабочих была выше 85%?