
- •Тема № 1. Основы теории четырехполюсников и многополюсников
- •Многополюсники и цепи с многополюсными элементами.
- •Основные уравнения теории четырехполюсников и их первичные параметры.
- •Входное и выходное сопротивление четырехполюсника.
- •Характеристические параметры четырехполюсника: входное и выходное сопротивление, постоянная передачи.
- •2.2 Фильтры верхних частот. Полосовые фильтры.
- •2.2. Определение частот среза, согласование каскадов фильтра между собой и с нагрузкой.
Тема № 1. Основы теории четырехполюсников и многополюсников
Многополюсники и цепи с многополюсными элементами.
В теории четырехполюсников исследуются общие свойства цепи по отношению к внешним выводам независимо от конкретного вида схемы.
Для
этого устанавливаются соотношения
между двумя парами напряжений и токов:
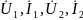 входа
и выхода, которые полностью характеризуют
поведение цепи относительно выводов.
входа
и выхода, которые полностью характеризуют
поведение цепи относительно выводов.

Из этих 4 величин лишь две любых являются независимыми. Уравнения четырехполюсников выражают остальные две величины (неизвестные) через известные. Число таких уравнений равно
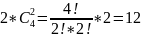
или 6 систем уравнений по 2 в каждой системе.
Коэффициенты этих уравнений называют параметрами 4х-полюсников.
Основные уравнения теории четырехполюсников и их первичные параметры.
Уравнения и параметры четырехполюсников.
а) система Y-параметров
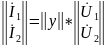
или
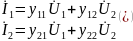
Входные проводимости:
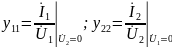
Передаточные проводимости:
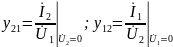
В
цепях, удовлетворяющих принципу
взаимности:
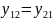 .
.
Поведение
таких четырехполюсников определяется
тремя параметрами. Если дополнительно
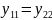 ,
то получим симметричный четырехполюсник,
имеющий лишь два независимых параметра.
,
то получим симметричный четырехполюсник,
имеющий лишь два независимых параметра.
б) системы Z – параметров
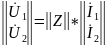
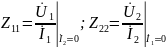 -
входные сопротивления;
-
входные сопротивления;
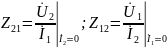 -
передаточные сопротивления.
-
передаточные сопротивления.
В
обратных цепях:
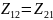 (три независимых параметра).
(три независимых параметра).
Дополнительно
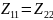 – симметричный четырехполюсник с двумя
независимыми параметрами. Параметры
сопротивлений являются дуальными
параметрами проводимостей.
– симметричный четырехполюсник с двумя
независимыми параметрами. Параметры
сопротивлений являются дуальными
параметрами проводимостей.
в) система A – параметров (параметры передачи).
Разрешая
систему (*) относительно
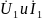 :
:
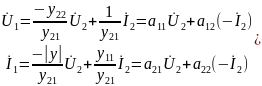
где параметры передачи:
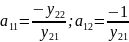
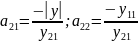
где
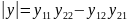
Таким образом, параметры одной системы четырехполюсника могут быть выражены через параметры другой системы того же четырехполюсника.
Для обратимых четырехполюсников:
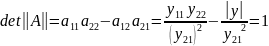 ,
,
так
как
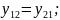
для
симметричных четырехполюсников:
=>
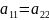
Смысл параметров A определяется опытами холостого хода и короткого замыкания на зажимах четырехполюсника:
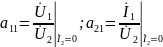
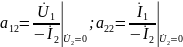
В
режиме холостого хода на выходе
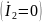 напряжение и ток на входе:
напряжение и ток на входе:
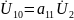 ;
;
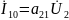
а
в режиме короткого замыкания
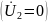 напряжение и ток на входе:
напряжение и ток на входе:
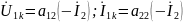
Систему (**) можно рассматривать как наложение режимов холостого хода и короткого замыкания:
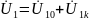
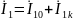
Систему (**)
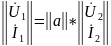
можно преобразовать к виду
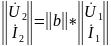
где
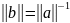 ,
то
есть
,
то
есть
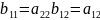
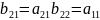
г) смешанные системы параметров
h-параметры:
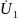 =
=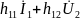
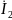 =
=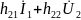
Причем
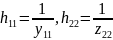
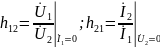
Для
обратных цепей:
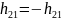
g-параметры:
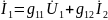
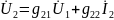
Причем
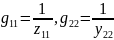
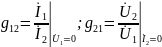
Для
обратных цепей:
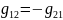 ;
и для симметричных четырехполюсников:
;
и для симметричных четырехполюсников:
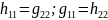
Два четырехполюсника называют эквивалентными, если их параметры одинаковы.
Входное и выходное сопротивление четырехполюсника.
Методы расчета параметров четырехполюсника:
Используя методы теории цепей, исключая параметры внутренних узлов и контуров схемы из уравнений;
По физическому смыслу – из опытов холостого хода и короткого замыкания.
Пример:
Рассчитаем Y-параметры П-образного четырехполюсника:
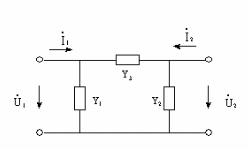
При коротком замыкании выхода:
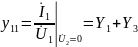
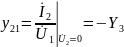
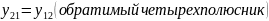
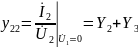
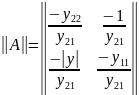
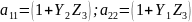
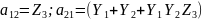
Для T-образной схемы параметры сопротивлений будут дуальными:
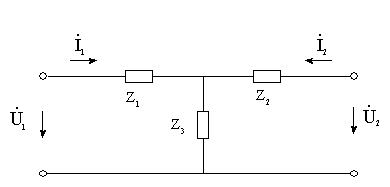
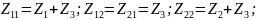
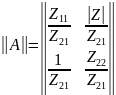
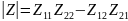
Получаем:
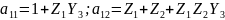
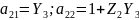
1.6 Соединения четырехполюсников.
Схема четырехполюсника сложной структуры может быть составлена из нескольких четырехполюсников более простой структуры путем соединения их выводов.
а) каскадное усиление
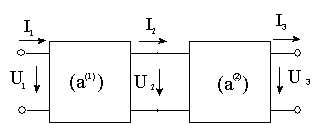
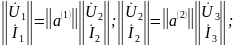
то есть
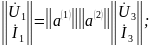
то есть
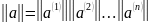
б) параллельное соединение
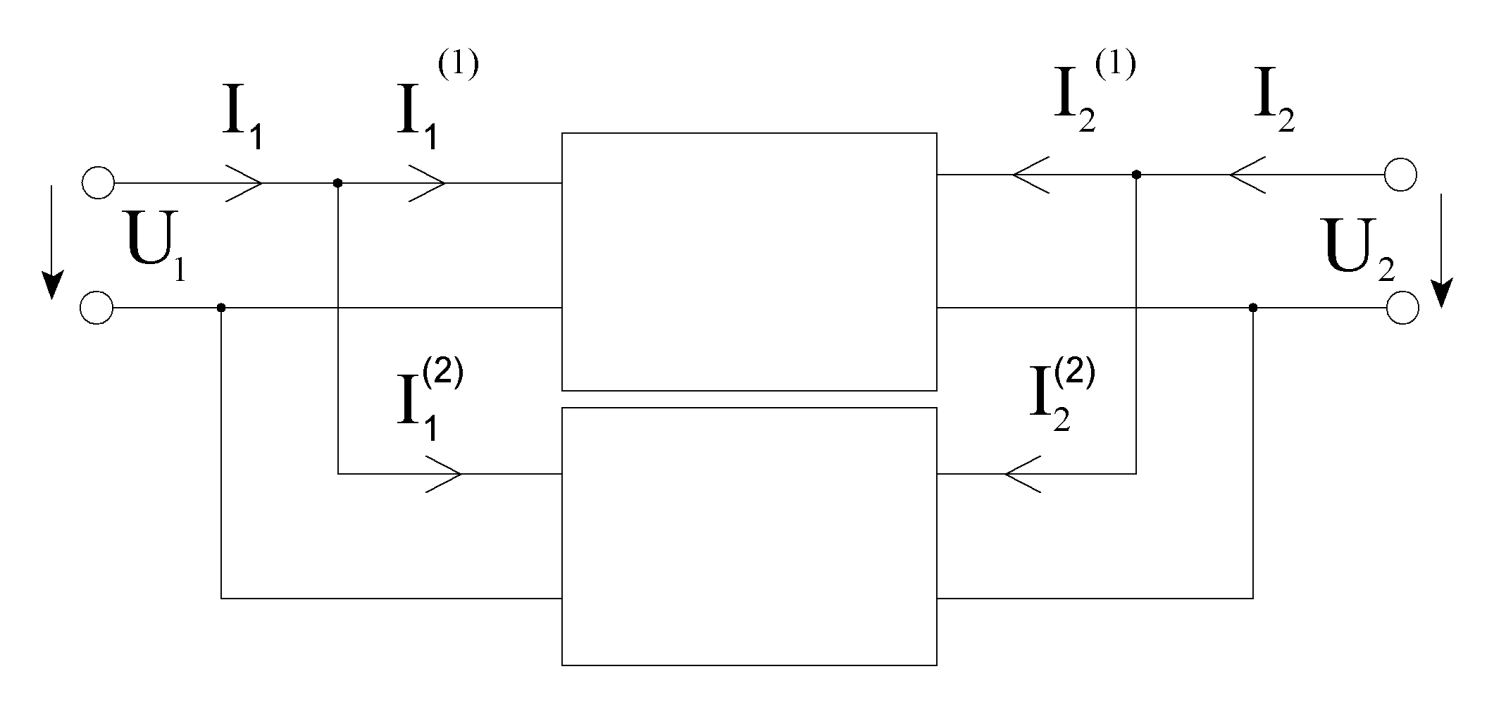
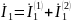
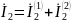
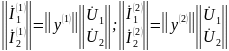
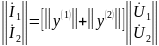
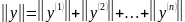
в) последовательное соединение
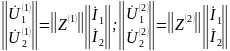
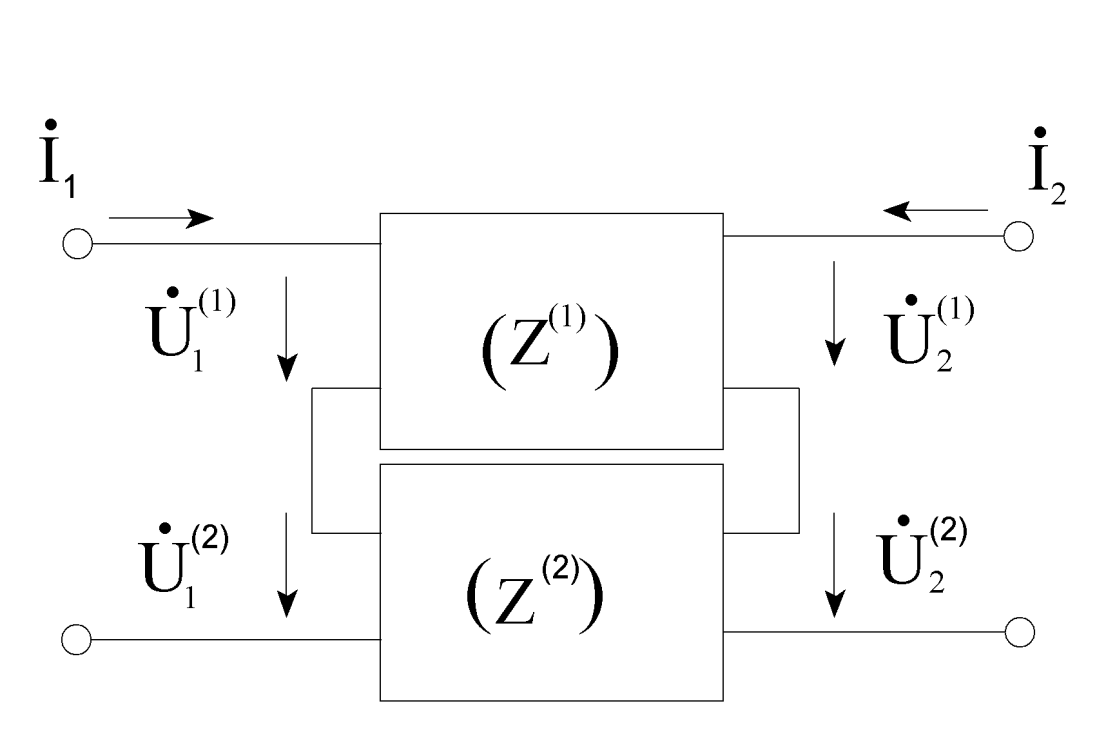
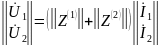
В общем случае
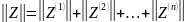
Анализ сложной схемы можно производить путем ее разбиения на более простые по структуре четырехполюсники.
Пример:
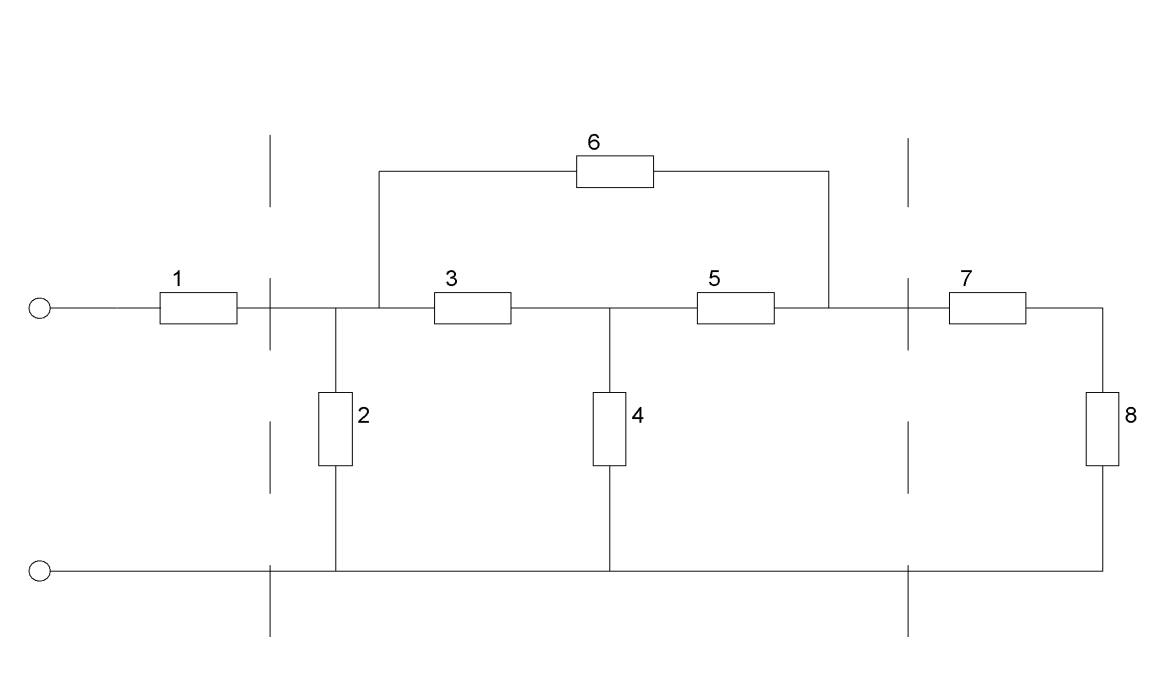
Средняя часть схемы: параллельно соединенный Т-образный четырехполюсник (3-4-5) и неуравновешенного четырехполюсника, состоящего из ветви (6) (выводы на входе и выходе нижние соединены между собой). К ним каскадно соединены два Г-образных четырехполюсника.
Функции передачи и функции входного сопротивления нагруженных четырехполюсников.
Изобразим схему нагруженного четырехполюсника
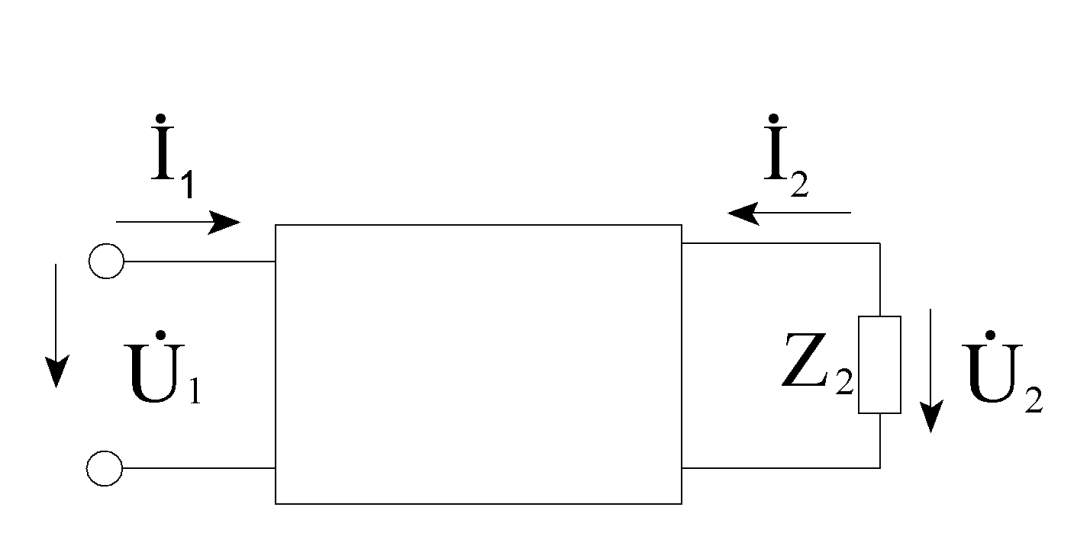
Z2 – двухполюсник нагрузки:
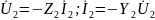
Функция передачи по напряжению
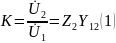
где
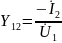 - передаточная проводимость
четырехполюсника.
- передаточная проводимость
четырехполюсника.
Функция передачи по току:
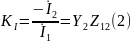
где
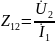 - передаточное сопротивление
- передаточное сопротивление
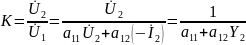
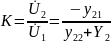
(связь a и y параметров)
Аналогично:
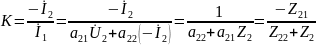
где
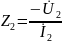
Функции передачи нагруженного четырехполюсника определяются только двумя его параметрами передачи
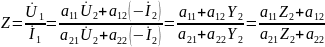
В частных случаях короткого замыкания (Z2=0) и разрыва (Y2=0) выхода четырехполюсника получаем входное сопротивление и входную проводимость
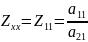
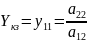
Функции цепи (то есть входные или передаточные), представляющей из себя четырехполюсник, состоящий из конечного числа элементов со сосредоточенными параметрами, является рациональной дробью от комплексной частоты:
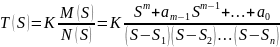
где Sk – полюса функции цепи или частоты собственных колебаний цепи. Докажем это.
Дифференциальное уравнение, связывающее напряжение и ток во входном контуре линейной цепи общего вида:
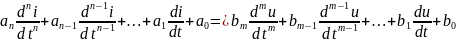
Пример: колебательный контур
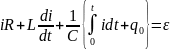
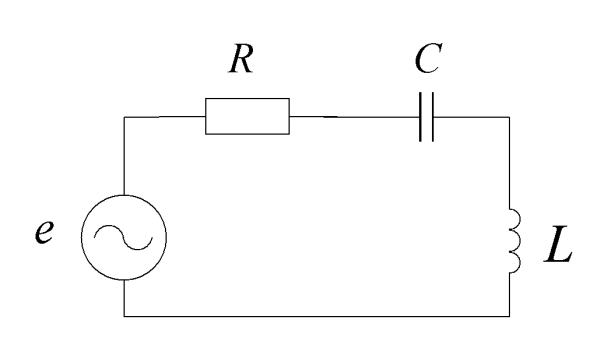
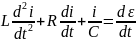
Комплексы напряжения и тока цепи:
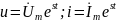
где S=α+jω – комплексная частота.
Они являются комплексными представлениями действительных сигналов в цепи:
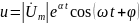
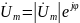
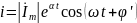
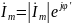
Подставляя u и i в уравнение, получим:
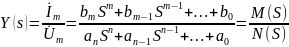
то есть комплексная функция цепи, в частности – входная проводимость, является рациональной дробью.
В зависимости от вида источника сигнала следует различать два случая свободного режима в цепи:
Режим короткого замыкания входных зажимов (при действии источника напряжения)
Режим разрыва входных зажимов (при действии источника тока)
В первом случае:
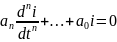 или
или
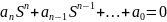 или
или
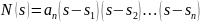
где Sk – корни характеристического уравнения, представляющие частоты собственных колебаний в режиме короткого замыкания входных зажимов.
Пример:
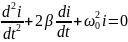
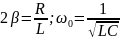
Подставим:
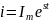
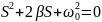
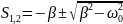
Если
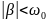
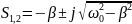
Собственные частоты (комплексные)
Для входного контура можно менять роли реакции и функции возбуждения. Поэтому во втором случае свободного режима
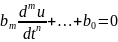 или
или
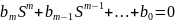 или
или
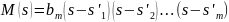
где s’k – корни характеристического уравнения, представляющие частоты собственных колебаний в режиме разрыва входных зажимов.
Вывод: комплексная функция цепи позволяет определять не только реакцию цепи в установившемся режиме, но также- и характеристическое уравнение свободного режима(её знаменатель содержит в себе частоты собственных колебаний цепи).
Перепишем выражение для комплексной входной проводимости:
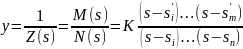
K=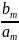
Частоты
собственных колебаний цепи при разрыве:
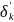 и коротком замыкании
и коротком замыкании
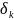 входных зажимов принято называть нулями
и полюсами функции.
входных зажимов принято называть нулями
и полюсами функции.
Нули входной проводимости являются полюсами входного сопротивления и обратно.
Проводимость
передачи:
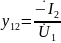
Определяем ток выхода при действии источника напряжения на входе.
Сопротивление передачи:
Определяем напряжение выхода при действии источника тока на входе.
Свободными режимами для них будут соответственно, режимы короткого замыкания и разрыва входных режимов.
Поэтому полюсы проводимости передачи совпадают с полюсами входной проводимости, а полюсы сопротивления передачи- совпадать с полюсами входного сопротивления, то есть с нулями входной проводимости.
Нули же функций передачи представляют те частоты, при которых передаваемый от входа к выходной ветви сигнал в виде тока или напряжения обращается в нуль.
Пример:
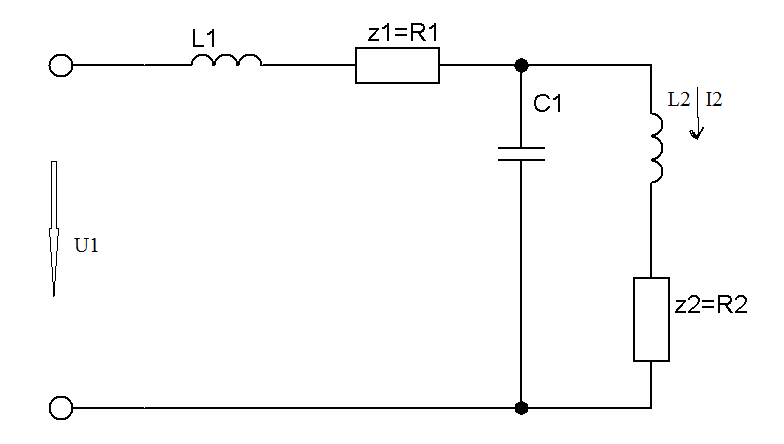
Ток и напряжение на выходе обращаются в нуль при тех s когда сопротивления последовательных ветвей стремится к бесконечности, а сопротивление параллельных ветвей стремится к нулю, соответственно:
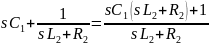
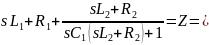
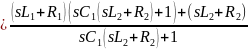
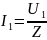
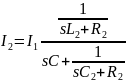
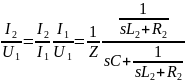
передаточная проводимость.
