6. Изгиб с кручением

6.1 Круглые валы

Силы, действующие на валы (давление на зубья шестерен, натяжение ремней, собственный вес вала и шкивов и т. п.), вызывают в поперечных сечениях валов следующие внутренние си­ловые факторы: М_кр = М_х , М_у , М_х , Q_y , Q_z . Таким образом, в лю­бом поперечном сечении одновременно возникают нормальные на­пряжения от изгибов в двух плоскостях, а также касательные напря­жения от кручения и поперечных сил.

Для расчета вала в первую очередь необходимо установить опасные сечения. С этой целью должны быть построены эпюры изги­бающих моментов М_у, М_z и крутящего момента М_кр.

Нагрузки, действующие на вал, разлагаем на составляющие вдоль координатных осей, а затем строим эпюры: от сил Р_1z , P_2z— эпюру M_y , от сил Р_1y, P_2y — эпюру M_z (рис. 29 , б и в).

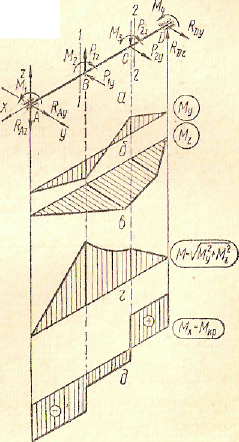Рис.29

При изгибе вала круглого или кольцевого сечения в каждом из его сечений имеет место прямой изгиб под действием результи­рующего изгибающего момента.( Рис.30 )

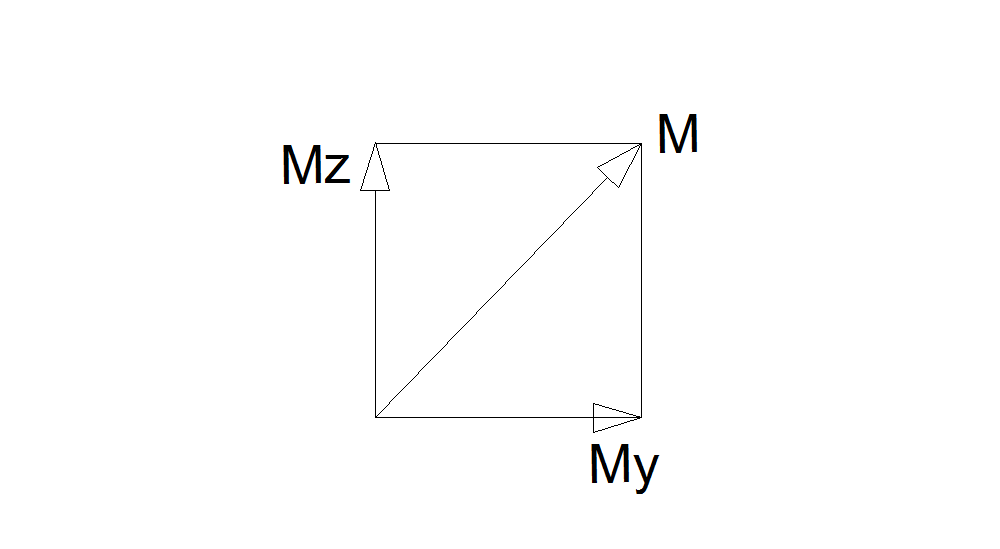
Рис.30 М =

Направление вектора результирующего момента определим, вычислив угол α между вертикальной осью Z и М из

Вектор момента М в разных сечениях может иметь различные на­правления, в силу чего даже при отсутствии распределенных нагру­зок эпюра М может быть криволинейной (рис. 29, г). Это позволяет строить эпюры М упро­щенным способом, несколько завышая значения суммарного изгибающего мо­мента М на участках между переломами эпюры: величины суммарного изгибаю­щего момента М вычисляют лишь для тех сечений, в которых на эпюрах М_у и М_z есть переломы. Эти величины от­кладывают в масштабе по одну сторону от оси на эпюре М и соединяют кривой линией (участок между 1 и 2 сечениями).

Далее строим эпюру M_КР = М_х (рис.29, д) и ищем опасные сечения, в которых одновременно велики М и М_кр. Сопоставляя эпюры, построенные в од­ном масштабе, находим, что опасным бу­дет сечение 1—1 или 2—2.

Теперь в опасном сечении нужно най­ти опасные точки.

Определим положение нейтральной линии (β = α) и строим эпюры нормаль­ных напряжений от результирующего изгибающего момента М (рис. 31), которые изменяются пропорционально расстоянию точек от нейтральной линии. Очевидно, опасными являются точ­ки А и В, наиболее удаленные от нейтральной линии,— в них одновременно и нормальные напряжения от изгиба и касательные напряжения от кручения имеют наибольшие значения: = = τ_мах =

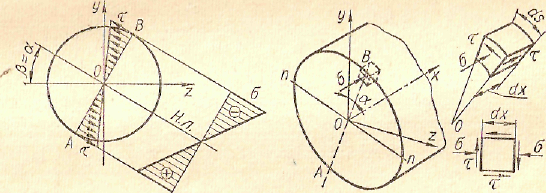
Рис. 31 Рис.32

У наиболее опасной точки В выделим элемент (рис. 32). По че­тырем его граням действуют касательные напряжения, а к двум из этих граней приложены еще и нормальные напряжения. Осталь­ные две грани свободны от напряжений. Таким образом, при изгибе с кручением элемент в опасной точке находится в плоском напря­женном состоянии. Аналогичные напряжения на гра­нях мы имели при изучении главных напряжений в изгибаемом бру­се, поэтому здесь главные напряжения нужно определять по тем же формулам:

σ₁ = (σ + ) ; σ₂ = 0 ; σ₃ = (σ - )

Заметим, что в данном случае сложного напряженного состоя­ния влиянием касательных напряжений от поперечных сил прене­брегаем, так как они значительно меньше касательных напряжений, вызванных кручением.

Для проверки прочности элемента, выделенного у опасной точ­ки, нужно, выбрав соответствующую теорию прочности, восполь­зоваться одной из формул для определения эквивалентного напряжения, например по четвертой теории прочности:

σ_{экв IV}= ≤ [σ] Подставляя значение и τ_мах и учитывая, что W_ρ = 2W получим:

σ_{экв IV}= ≤ [σ]

Числитель этой формулы представляет собой приведенный момент, действие которого эквивалентно совместному действию трех момен­тов (согласно принятой теории прочности). Следовательно, в случае необходимости подобным же образом можно получить формулы для приведенных моментов и по другим теориям проч­ности.

Нетрудно заметить, что теперь условия прочности можно заменить одной простой формулой: σ_{экв IV} = ≤ [σ]

Таким образом, при совместном действии изгиба с кручением стержни круглого сечения рассчитывают на изгиб от приведенного момента М_прив .

6.2 Брус прямоугольного сечения.

На практике часто встречаются стержни некруглого сечения, подверженные действию крутящих и изгибающих моментов. При загружении такого бруса, например, систе­мой сил Р₁ и Р₂ (рис,33 , а), вызывающих в сечении моменты М_Х М_у и М_кр, расчет проводят по следующей схеме. Внешние силы раскладывают на составляющие, при­водя их к оси вала. Для нахождения опас­ного сечения строят эпюры М_х, М_у и М_кр(рис,33 , б).

Установив по эпюрам опасное сечение 1—1, расположенное левее точки приложения силы Р₂, находят опасную точ­ку в нем, для чего строят эпюры напря­жений от всех силовых факторов (рис.34, а, б, в, г, д, е): б(М_х), в(М_у}; г(Q_х) ; д(Q_у); е(Mкр).

Эпюра е(Мкр) для длинной стороны кон­тура имеет максимум, который обозначим τ_мах(М_кр). Наибольшую ординату эпюры е(М_кр) на короткой стороне обозначим τ_мах¹(М_кр). Эти напряжения

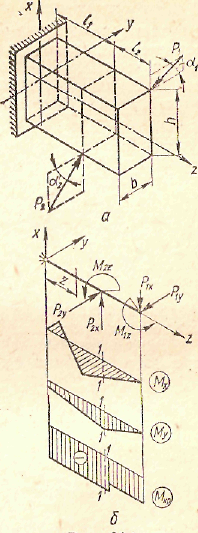
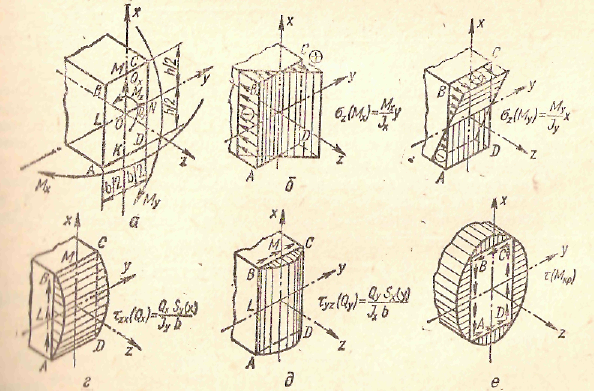
Рис 33 Рис.34

можно рассчи­тать по известным формулам кручения брусьев прямоугольного сечения.

τ_мах(М_кр) = τ_L = τ_N = ; τ_мах¹(М_кр) = τ_m = τ_K = γ· τ_мах

В данном случае σ_мах от изгиба не совпадают с τ_мах от кручения, поэто­му для выявления одной опасной точки приходится рассматривать со­четание напряжений в нескольких точках. Обычно бывает достаточно трех точек: одной из угловых (А или С), одной посредине длинной (L или N) и одной посредине короткой (М или К) сторон прямоуголь­ника. Так, для точек С, L, К

σ_c= + ≤[σ] ; τ_L= ± ; τ_K = (γ ± ;

Обычно касательные напряжения от поперечных сил малы и ими можно пренебречь.

Эквивалентные напряжения в точках L, и К согласно IV теории прочности и теории Кулона—Мора равны: в точке L

≤[σ] ≤[σ]

В точке К

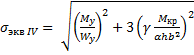≤[σ] ≤[σ]

Таким образом, наиболее опасная точка определяется только в ре­зультате вычисления эквивалентных напряжений во всех трех точках (С, L и К). При этом в каждом конкретном случае положение наиболее опасной точки зависит от соот­ношения моментов М_х, М_у и М_кр.

7. Общий случай действия сил на брус.

Если в сечении стержня дейст­вуют осевая сила N_z, изгибающие моменты в главных плоскостях М_х и M_{y ,} а также крутящий момент М_kp , то условие прочности, например по IV теории прочности, в точке К (рис, 34, а) будет:

σ_{экв IV}= ≤[σ]

аналогично в точке L

σ_{экв IV}= ≤[σ]