5. Кручение со сдвигом
Винтовые пружины – наиболее распространенный в технике тип пружин. Чаще всего их изготавливают из стальных стержней круглого поперечного сечения (проволоки).
Рис.25
На рис. 25 изображена цилиндрическая винтовая пружина, состоящая из n витков, загруженная силой Р. Пружина имеет средний диаметр D = 2R . Диаметр проволоки, из которой она изготовлена d. Отрежем ее часть сечением, перпендикулярным оси проволоки (рис.26).
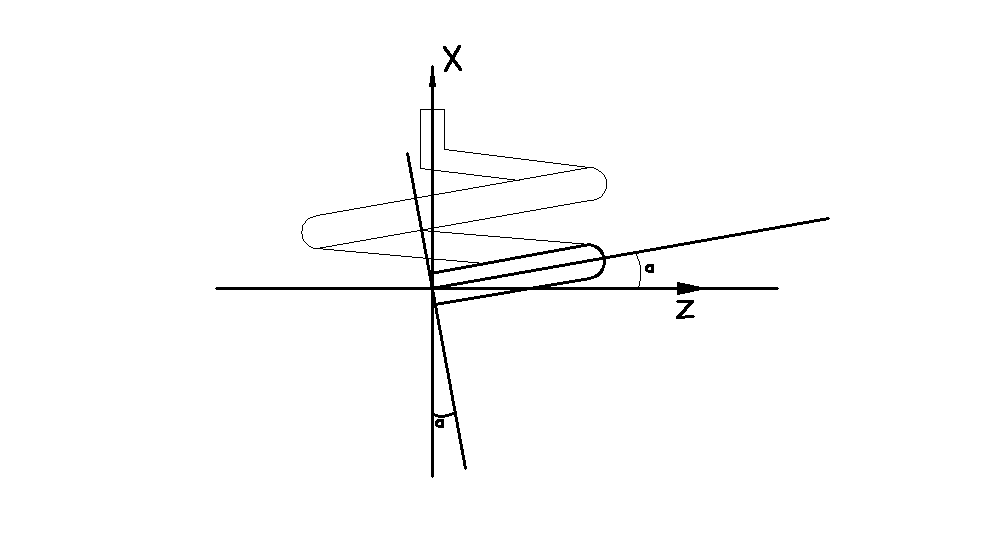
Рис.26
При взгляде со стороны оси у видно, что сечение, перпендикулярное касательной, наклонено к оси х под тем же углом α, что и касательная к оси проволоки к оси z. Если считать угол α бесконечно малым, то внутренние усилия можно свести к двум составляющим: поперечной силе Q = P, и крутящему моменту Mкр = P·R , а плоскость сечения будем считать вертикальной.
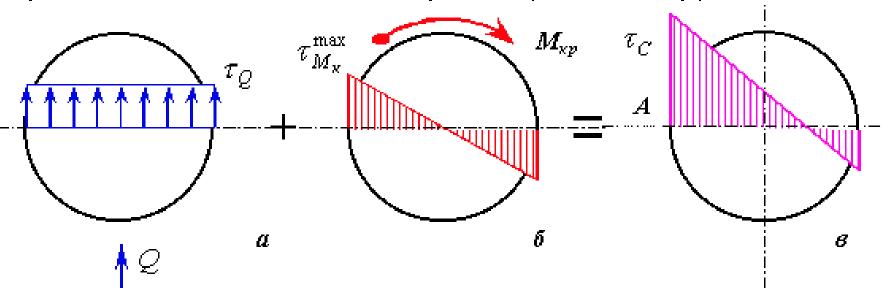
Рис.27
Касательные напряжения от поперечной
силы равномерно распределены по всему
сечению и определяются как: τ(Q)
= 
=
(Рис.27а)
Касательные напряжения от крутящего
момента достигают максимального
значения на поверхности проволоки
и определяются как: τmax(M)
= 
=
(Рис.27б)
Направления касательных напряжений
совпадают на внутренней поверхности
витка в точке А,
и именно здесь
суммарное напряжение τс
=
τ(Q)+
τmax(M)=
+ 
(Рис.27в)
или
τс
= 
(1+
)
Условие прочности имеет вид τс = (1+ ) ≤ [τ]
Во многих случаях для пружин, изготовленных
из тонкой проволоки с большим и средним
радиусом R
отношение 
<< 1
а следовательно доля в
суммарном напряжении составляющей от
поперечной силы мала, и ею можно
пренебречь.
Например, при 
0,5
см, а R= 10 см
= 0,0125 Т.е касательное напряжение
от поперечной силы составляет от
максимального касательного напряжения,
вызываемого крутящим моментом 1,25%.
В точном приборостроении и машиностроении, при расчете пружин кроме влияния поперечной силы необходимо учитывать: продольную силу и момент изгибающий, возникающие при учете величины угла α; разницу радиусов кривизны внутренних и наружных волокон витка. Кроме того существуют пружины другой формы: конические, призматические, параболические, двойные конические, бочкообразные и т.д. Шаг пружин может быть переменным, а форма сечения отличной от круглой. Методы расчета таких пружин достаточно сложны, и рассматриваются в специальной литературе.
При определении удлинения пружины (или осадки) λ, как правило, учитывают только кручение витков. Вырежем элементарную часть витка длиной ds плоскостями проходящими через ось пружины, и будем считать, что плоскости сечений перпендикулярны оси проволоки и вертикальны.
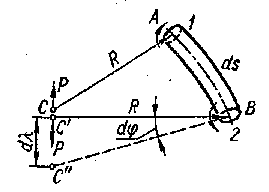
Рис.28
Отрезки
АС и ВС1 на рис.28
являются радиусами витка. Тогда под
действием крутящих моментов, приложенных
в сечениях, проволока будет
закручиваться, и если считать радиус
АС неподвижным, то точка С1
радиуса ВС1 переместится
вдоль оси Х в точку С11.
Тогда С1 С11
является элементарной составляющей
осадки. С1 С11
= dλ ≈ R·
Здесь
угол поворота радиуса ВС1
является углом закручивания участка
ds
и определяется по формуле угла
закручивания при кручении
=
ds
где Mкр=PR
; Iρ
=
Т.к. скручиваются все витки проволоки, имеющие общую длину s =2πRn , то полную осадку пружины можно определить интегрированием по длине
λ
= 
R
= 
Полученные
выражения можно использовать при
составлении условия жесткости пружины.
При расчете амортизационных пружин возникает необходимость знать величину энергии, которую способна поглотить пружина, не разрушаясь. Потенциальная энергия деформации пружины может быть определена по формуле
U=
Pλ
=
Величину крутящего момента
можно выразить через напряжение Мкр=
PR = 
Тогда
потенциальную энергию, накапливаемую
в пружине тоже можно выразить через
напряжение: U
= 
Учитывая,
что обьем материала пружины равен
V
=
U
= 
V
Задаваясь предельной величиной
напряжения 
можно вычислить обьем пружины,
необходимый для поглощения заданной
величины энергии U
в пределах допустимых значений
напряжения. V
=
