2. Косой изгиб.

Пусть на стержень прямоугольного поперечного сечения действует один изгибающий момент M , плоскость действия которого не совпадает с плоскостями главных осей сечения. (рис.15) Угол α является углом между плоскостью действия момента и главной осью у сечения, и

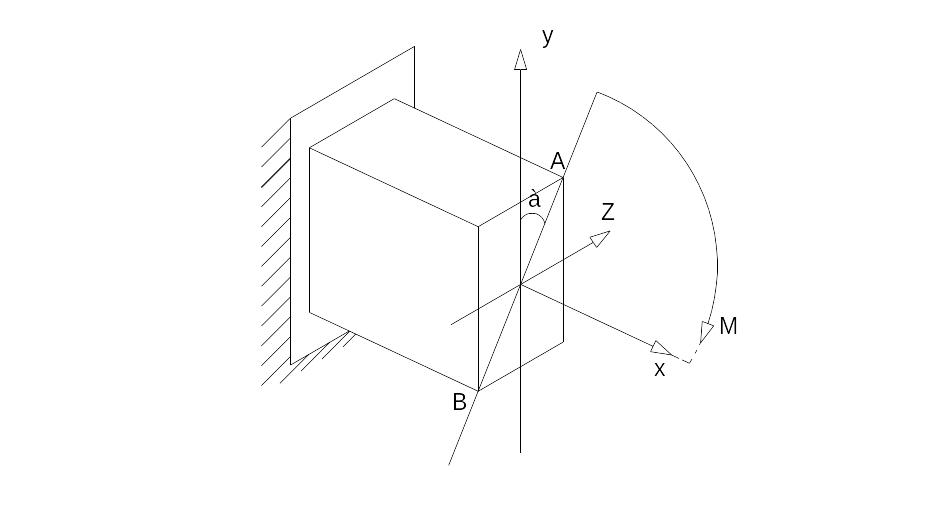
Рис 15

определяет положение силовой линии в плоскости поперечного сечения. В нашем случае справедливы зависимости М_z = M M_y = M

Напряжения в любой точке поперечного сечения при одновременном действии М_z и M_y могут быть определены как σ = y + = y + = M( +

Применяя эту формулу, следует учитывать знаки координат точки и знаки моментов М_z и M_y определяющихся положением растянутых и сжатых волокон.

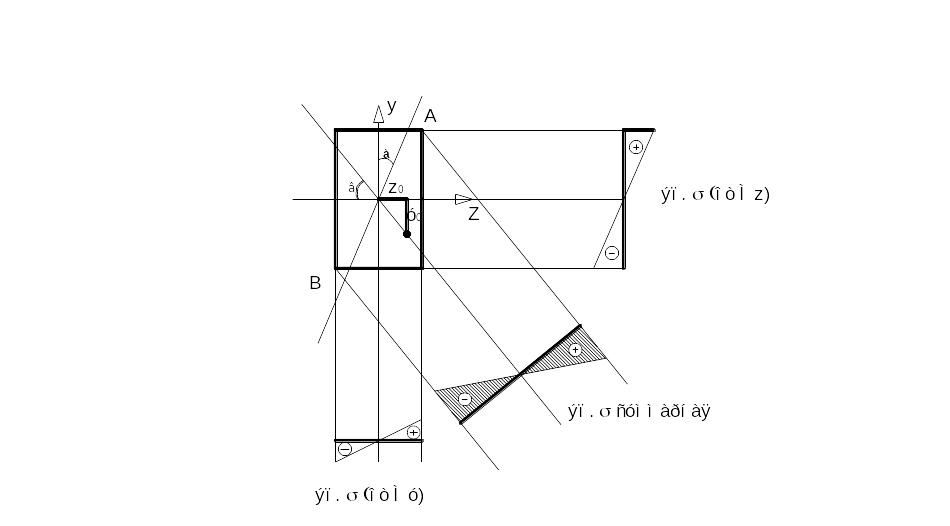Рис 16

Для простых сечений определить положение опасных точек не составляет труда, а для сложных составных сечений требуется выполнить следующие действия.

Определим положение нейтральной оси, на которой напряжения равны нулю, приравняв нулю выражение напряжений.

σ = M( + =0 т.к. М≠0 то + = 0 здесь y и координаты точки лежащей на нейтральной оси. Обозначим их как y₀ и ₀ . Перенесем вправо от знака равенства и преобразуем выражение следующим образом.

= - · т.е. = - · Здесь тангенс угла между нейтральной осью и осью Получим его значение =

Из формулы видно, что в общем случае сложного изгиба при I_z ≠ I_y нейтральная ось не перпендикулярна к силовой линии, но они всегда проходят через смежные квадранты. После того, как определено положение нейтральной линии находим положение опасных точек, как наиболее удаленных от нейтральной оси ( точки А и В).

В данном случае в точке А возникает наибольшее растягивающее напряжение, а в точке В наибольшее сжимающее.

Условия прочности имеют вид σ_мах=σ_а = y_а + _а ≤[σ_раст]

σ_мин=σ_в =- y_в - _в ≤[σ_сжат]

Рис. 17

Перемещения при косом изгибе определяются по принципу независимости действия сил. Если W - прогиб в направлении главной оси У; V – прогиб в направлении главной оси , которые определяются любым известным нам способом. Величина полного прогиба может быть определена как геометрическая сумма прогибов в направлении главных осей.

f =

Направление полного прогиба перпендикулярно к нейтральной линии и, в общем случае, не совпадает с направлением силовой линии.

3. Изгиб с растяжением.

Рассмотрим случай, когда к стержню прямоугольного поперечного сечения приложены два изгибающих момента и центрально приложенная продольная растягивающая сила N. (Рис.18)

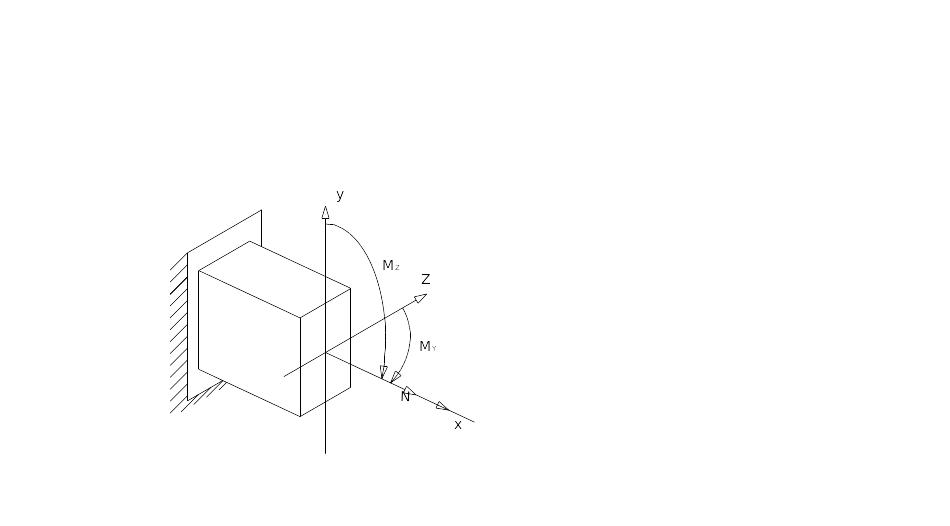
Рис. 18

Легко заметить, что от косого изгиба этот вид деформации отличается только дополнительно приложенной продольной силой. Используя принцип независимости действия сил, напряжения в любой точке можно определить как сумму напряжений действующих факторов по формуле:

σ = y +

Рис.19

Итоговая эпюра напряжений состоит из трех составляющих. На рис.19 видно, что нейтральная линия не проходит через центр площади, и разделяет сечение на две неравные растянутую и сжатую зоны. Наиболее удаленные от нейтральной оси точки А и В являются опасными. Для них составляем условия прочности.

σ_мах = σ_а = y_а + _а ≤ [σ_раст]

σ_мин = σ_в = - y_в - _в ≤ [σ_сжат]

Еще интереснее получаются загружения, когда моменты в сечении создаются не парой сил, а внецентренно приложенной продольной силой (растягивающей или сжимающей).