2. Абсолютно жесткие балки

Балку со свободными концами можно считать абсолютно жесткой, если соблюдается неравенство ℓ ≤ 1,2/ . Величина прогибов такой балки пренебрежимо мала по сравнению с величиной ее просадки в основание под действием приложенных нагрузок. Можно считать, что подошва балки, опирающаяся на основание( грунт) сохраняет прямолинейную форму, и эпюра прогибов имеет прямолинейное очертание. А следовательно и реакция основания распределена по линейному закону.

Для определения равнодействующей реакции основания и точки ее приложения воспользуемся уравнениями равновесия. Из суммы проекций всех сил на ось У найдем равнодействующую реакции основания R, а из суммы моментов относительно оси Z (проходящей через центр площади подошвы балки) эксцентриситет ее приложения. Обозначим величину эксцентриситета как - е. (Рис.11а)

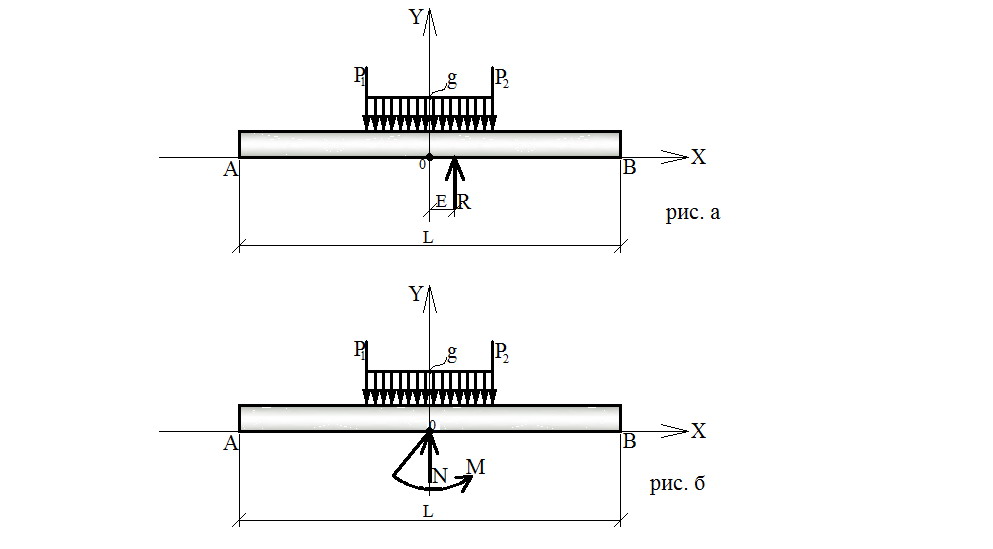
Рис.11

Воспользовавшись правилом параллельного переноса сил перенесем R в центр площади подошвы балки(рис.11а). При этом R заменяется центрально приложенной силой N = R, и момен-том М_z = R е причем момент направлен в ту сторону, куда вращает балку реакция R. В нашем примере все силы приложены к оси Х, т.е. создают момент только относительно оси Z. (Рис.12)

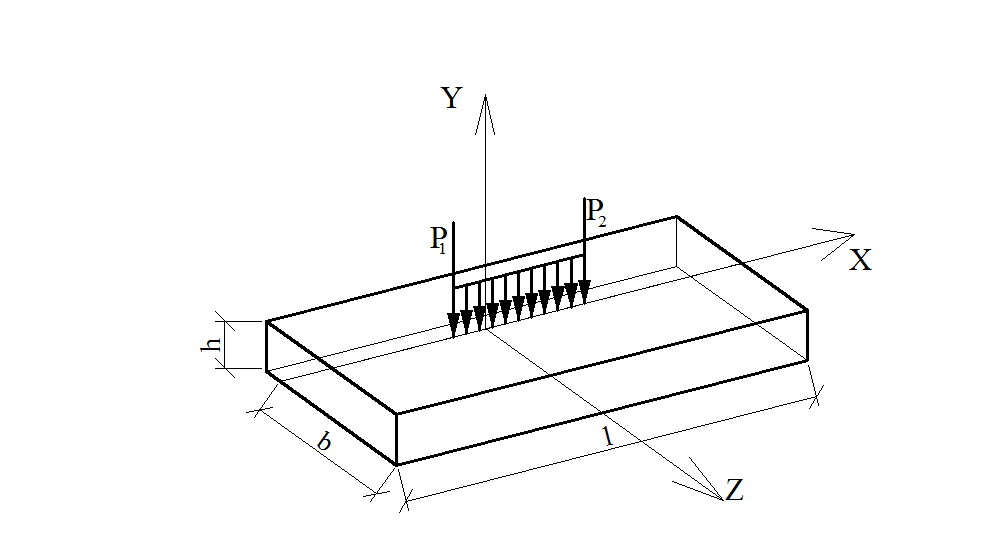
Рис.12

От воздействия центрально приложенных реактивных N и М_z подошва балки испытывает сжатие и изгиб. Определим нормальные напряжения в подошве балки направленные вдоль оси У и построим их эпюры. Площадь подошвы А= ℓ b Напряжение от силы N определяется как σ_N = Напряжения от изгибающего момента в крайних точках σ_m = где W_z= Построим суммарную эпюру σ_сумм

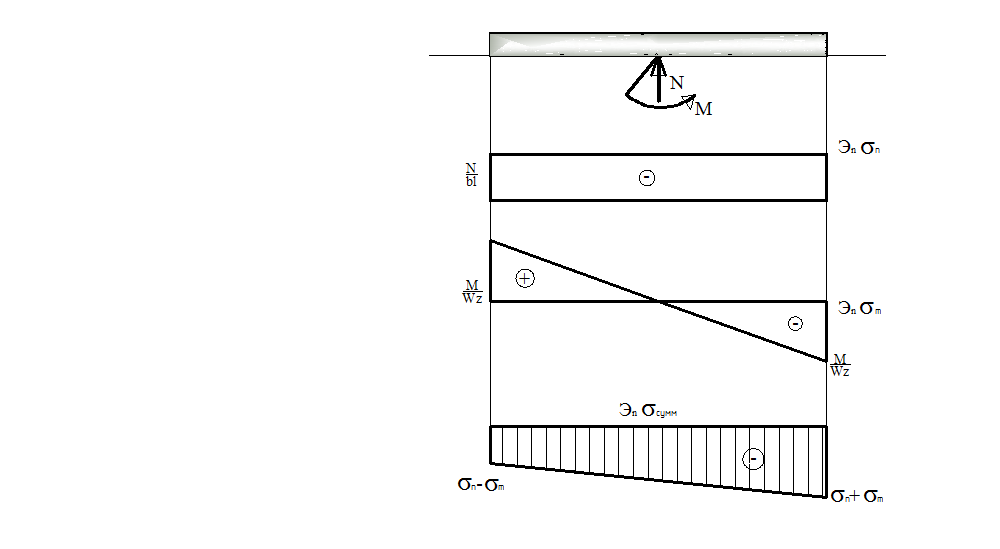
Рис.13

Напряжения распределены по площади подошвы балки. Для того, чтобы перейти к распреде-ленной вдоль оси Х реактивной нагрузке умножим значения суммарного напряжения на ширину балки. Получим интенсивности неравномерно распределенной реактивной нагрузки в крайних точках балки r_a и r_b

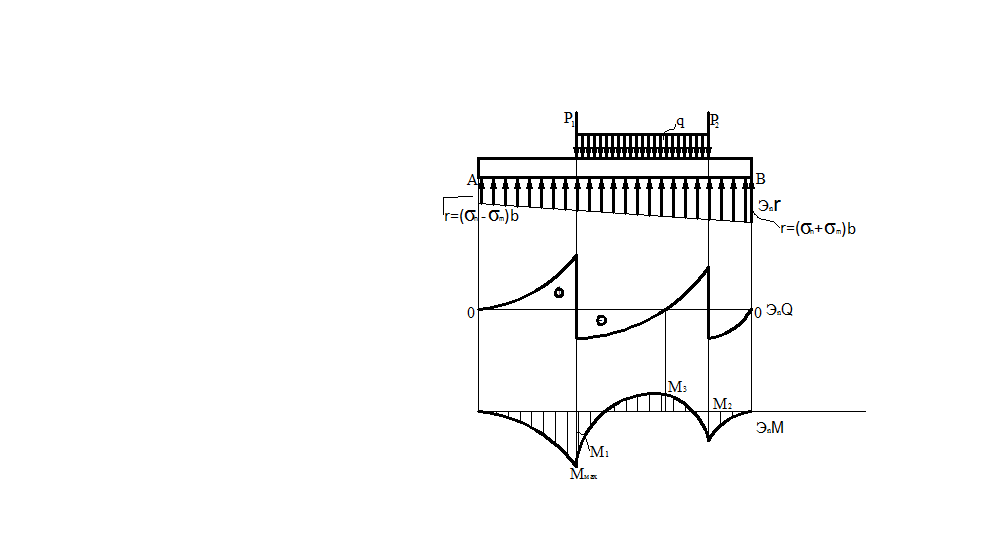
Рис.14

Построим эпюры внутренних силовых факторов возникающих в балке под действием активной и реактивной нагрузки. По ним определим положение опасных сечений и выполним прочностной расчет.

Необходимо помнить, что для определения типа балки необходимо было задаться толщиной балки. Следовательно, прочностной расчет выполняется как проверочный, а не проектировочный.

Тема 14 Сложные сопротивления

Литература:

Справочник по сопротивлению материалов. Писаренко Г.С. Глава 11

Сопротивление материалов. Писаренко Г.С. Глава 12

Вопросы:

1. Общие положения

2. Косой изгиб

3. Изгиб с растяжением

4. Внецентренное сжатие короткого бруса

5. Кручение со сдвигом

6. Изгиб с кручением

6.1Круглые валы

6.2 Брус прямоугольного сечения

7. Общий случай действия сил на брус

1. В первой части курса сопротивления материалов мы рассмотрели четыре простые деформации стержней: осевое растяжение(сжатие), сдвиг, кручение и плоский прямой чистый изгиб. В перечисленных деформациях в поперечном сечении стержней действует по одному внутреннему силовому фактору, каждый из которых реализуется в сечении либо нормальным, либо касательным напряжением. Появление двух разных напряжений свидетельствует о возникновении двух, принципиально отличных друг от друга способов разрушения тела.

Все случаи деформации стержней, при которых в поперечном сечении действует более одного внутреннего силового фактора, называются сложными сопротивлениями.

Следует различать две группы сложных сопротивлений.

К первой относятся такие сочетания внутренних силовых факторов, которые реализуются в сечении одинаковыми по виду напряжениями.

Нормальная сила N и изгибающий момент M реализуются в сечении нормальным напряжением σ. Этот вид сложного сопротивления называется изгибом с растяжением (сжатием) или внецентренным растяжением ( сжатием).

Возможно сочетание двух изгибающих моментов, действующих в разных плоскостях. Этот вид сложного сопротивления называется неплоским изгибом. Если действует один изгибающий момент, но плоскость его действия не совпадает ни с одной из главных плоскостей сечения, то его можно разложить на два, и этот вид изгиба называется косым.

Момент крутящий М_кр и поперечная сила Q реализуются в сечении касательными напряжениями τ. Этот вид сложного сопротивления называется кручением со сдвигом, и используется при расчете пружин.

Ко второй группе относятся такие сочетания внутренних силовых факторов, которые реализуются в сечении разными по виду напряжениями: нормальными и касательными. Например, сочетание момента изгибающего и момента крутящего называется кручением с изгибом.

Сочетание поперечной силы и изгибающего момента при поперечном изгибе тоже требует причислить этот вид деформации ко второй группе сложных сопротивлений.

К этой же группе относится и так называемый общий случай действия нагрузок, при котором действуют все силовые факторы одновременно.

Возникновение сложного напряженного состояния во второй группе сложных сопротивлений требует применения теорий прочности при расчете на прочность. Именно этим и отличается вторая группа от первой, в которой результат воздействия разных факторов просто суммируется.