2. Бесконечно длинная балка при действии нескольких нагрузок.

Для расчета балок на упругом основании применим принцип независимости действия сил, в соответствии с которым результат одновременного воздействия нескольких сил равен сумме результатов порознь действующих сил.

Если к балке приложена сила = 1 обозначим величину момента в произвольной точке как m₁ При увеличении нагрузки до Р значение момента возрастает до М₁ Причем М₁ = m₁

Рассмотрим два разных загружения одной и той же балки одинаковыми силами в двух разных точках, расположенных на расстоянии «а» друг от друга. (рис.5)

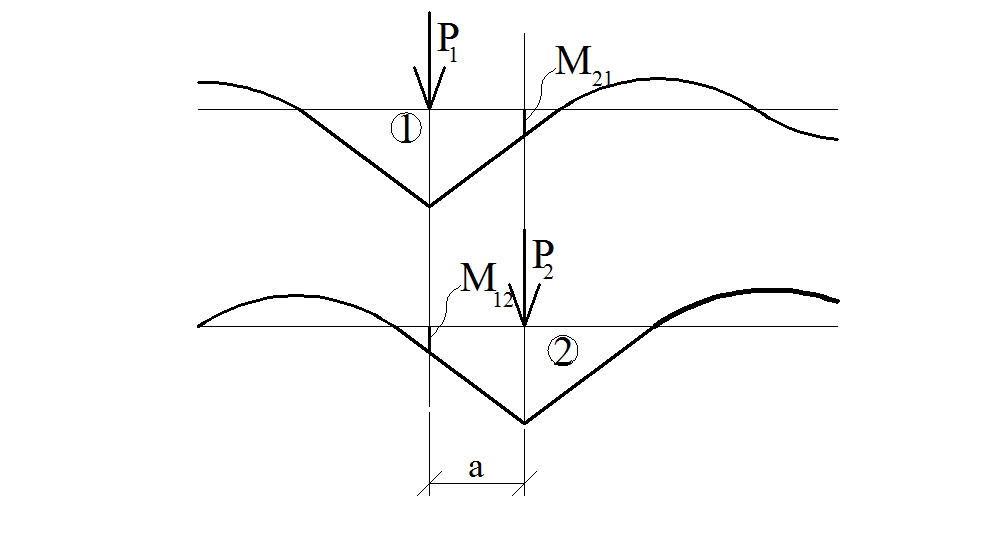
Рис.5

В силу симметрии эпюр моментов значение ординаты на первой эпюре под второй силой (М₂₁) равно значению ординаты на второй эпюре под первой силой (М₁₂). М₂₁= М₁₂

Пусть к балке приложены несколько сил и участок распределенной нагрузки (рис.6).

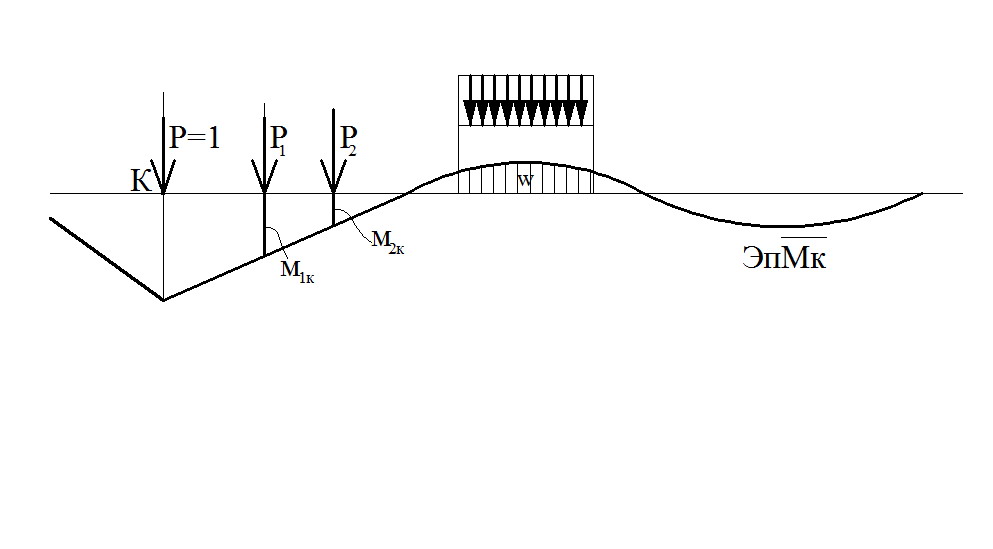
Рис.6

Обозначим на балке точку (к) в которой мы хотим найти значение изгибающего момента. Приложим в точке (к) единичную силу =1 и построим эпюру моментов от нее. Тогда под силами Р₁ и Р₂ значения ординат будут равны соответственно m_1к и m_2к . Тогда в силу ранее изложенного значение момента в точке (к) можно определить как М_к= Р₁ m_1к + Р_{2 2к}+ q ω

Где ω площадь участка эпюры моментов, расположенного под распределенной нагрузкой.

Для построения суммарной эпюры моментов от всех приложенных воздействий (рис.7) следует иметь в виду, что экстремальные значения ординат ,как правило, расположены под сосредоточенными силами. Вычислим значения ординат под силами, построим их и соединим плавными кривыми прогнутыми вверх. Это допустимо, потому, что в прочностном расчете значимыми являются наибольшие значения внутренних усилий. Выберем из всех значений наибольшее М_мах и используем его в условии прочности балки. σ = ≤ [σ]

2. Расчет коротких упругих балок.

Метод последовательных приближений.

Короткой упругой считается балка для которой выполняется условие 1,2/ < ℓ ≤ 4π/ Если для такой балки построить эпюры моментов или поперечных сил как для бесконечно длинной, то найденные значения M и Q на концах не будут пренебрежимо малыми. А в действительности, на свободных концах балки, они равны нулю. Знание точной величины внутренних усилий позволяет применить метод последовательных приближений. Но предварительно необходимо научиться находить моменты и поперечные силы в односторонне конечной упругой балке нагруженной на конце силой Р₀ и моментом М₀ .

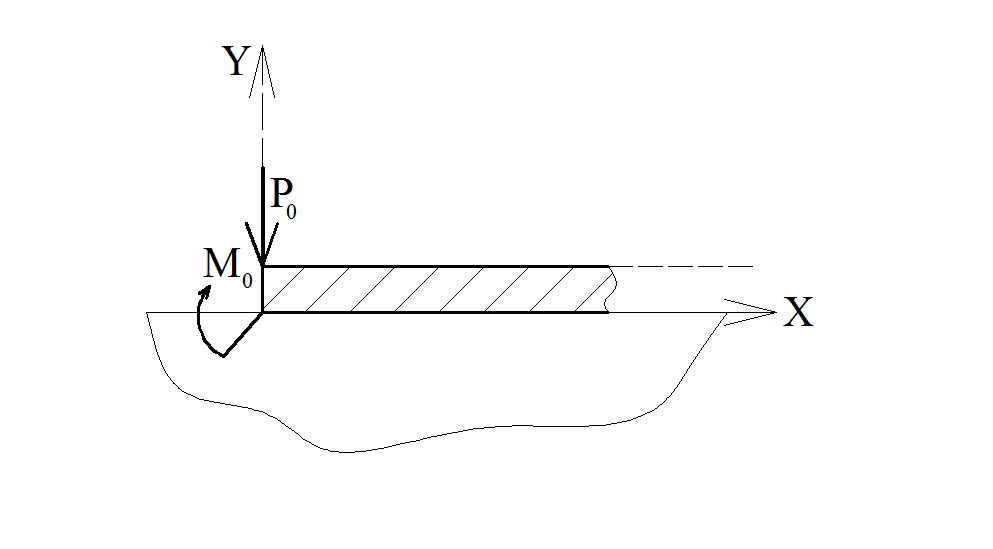
рис.8

Поместим начало координат в нагруженной концевой точке. Общий интеграл тот же

у = А

Из начальных условий при этом получаем 1) при Х = ∞ у = 0 отсюда А = В = 0 2) при Х =0 М_z(х) = EI_z из общего интеграла С = -

3) при Х=0 Q_(x) = EI_{z 0} отсюда получаем Д = - (Р_о - М_о

Т.е. М_z(х)= - (Р_о = - (Р_о - М_о

Q_(x) = - _о - (Р_о + 2 М_{о 3})

Полученные формулы позволяют найти моменты и поперечные силы в односторонне конечной балке от загружения силой и моментом на свободном конце.

Рассмотрим балку (рис. 9) длинной, ℓ = а + в; причем 1,2/ < ℓ ≤ 4π/

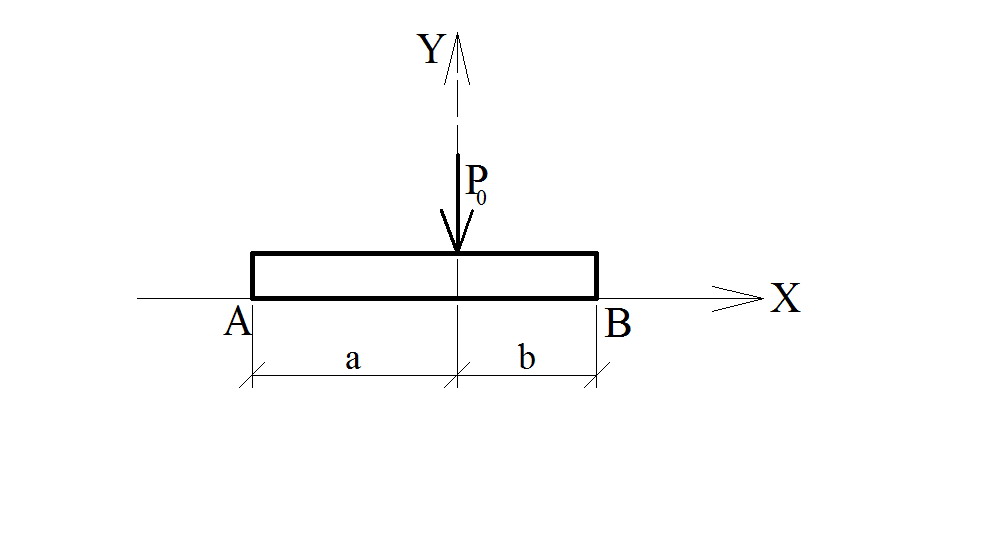
Рис. 9

Балка нагружена силой Р на расстоянии (а) от левого конца и (в) от правого. Найдем значения момента и поперечной силы в точках А и В как для бесконечно длинной балки, загруженной одной силой Q_a и M_a ; Q_b и M_b по формулам и Q =

Работа короткой балки, в соответствии с принципом независимости действия сил, может быть представлена как совокупность трех состояний: 1) бесконечно длинной в обе стороны, загруженной одной силой Р; 2) бесконечно длинной из точки А вправо, загруженной силой Р_о= - Q_a и моментом М_о= -M_a в точке А 3) бесконечно длинной из точки В влево, загруженной силой Р_о= -Q_b и моментом М_о =-M_b.

Найдем из второго состояния величины момента и поперечной силы в точке В M_b2 и Q_b2

Найдем из третьего состояния величины момента и поперечной силы в точке А M_а3 и Q_а3 Для вычисления используем формулы М_z(х)= - (Р_о - М_о ; Q_(x) = - (Р_о + 2 М_{о 3})

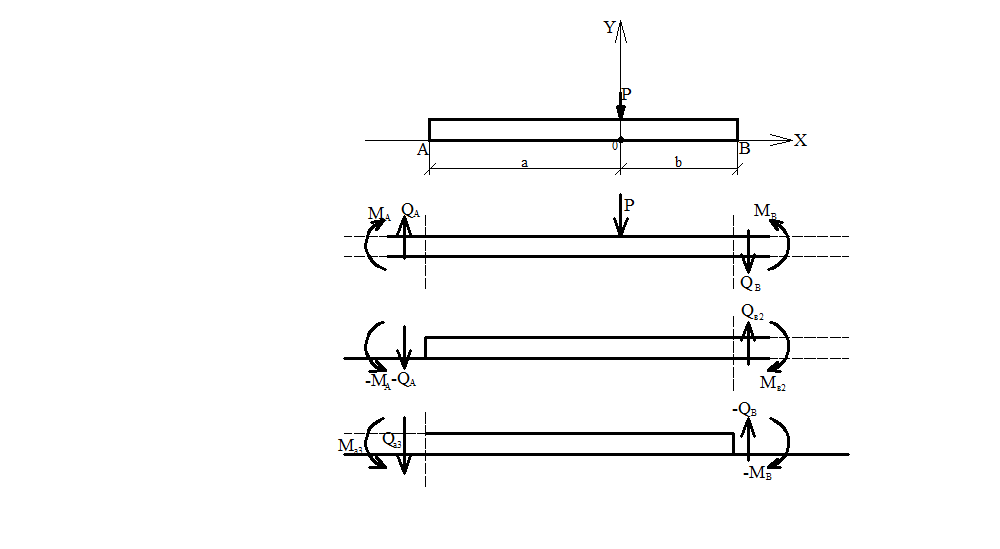
рис. 10

Просуммируем значения внутренних усилий в точках А и В всех трех состояний

Q_a+( - Q_a)+ Q_а3 = ΔQ_а Q_b+ (-Q_b) + Q_b2 = ΔQ_в

M_a+(-M_a) + M_а3 = ΔМ_а M_b+(-M_b)+ M_b2= ΔМ_в

Значения погрешностей ΔQ_а, ΔQ_в, ΔМ_а, ΔМ_в будут малыми, но не нулевыми. А должны быть таковыми на свободных концах балки. Внесем поправку в значения загружений, приложенных во втором и третьем состояниях на величины -ΔQ_а, -ΔQ_в, -ΔМ_а, -ΔМ_в и повторим действия. Вновь полученные погрешности должны быть меньше. Подбор можно заканчивать, когда величина погрешности будет достаточно малой или равной нулю. Теперь значения внутренних усилий в короткой упругой балке легко определить как сумму усилий в соответствующем сечении всех трех загруженных состояний. Задача легко решается при использовании вычислительной техники для любой наперед заданной величины погрешности.

Метод начальных параметров.

Общий интеграл или уравнение прогибов может быть записано и следующим образом:

Y = y_{o x} + θ_{o x} + M_o C_x + Q_o D_x+ f(x) где y_{o ,} θ_{o ,} M_{o ,} Q_o соответственно прогиб, угол поворота, момент изгибающий и поперечная сила в начале отсчета. f(x) – составляющая влияния нагрузок, приложенных на балку. Значения f(x) и ее производных для различных типов нагрузки, а также производные произвольных постоянных приведены в справочнике Рудицина на странице 239 в таблицах 8.2 = α₀ ∙b Произвольные постоянные находятся по формулам _x= _x= ( + C_x= D_x= ( -

Гиперболический синус - Гиперболический косинус -