Явление усталости материалов

Усталостью материалов называется явле­ние разрушения при многократном повторении напряжений.

Способ­ность материалов сопротивляться разрушению при повторно-перемен­ных напряжениях называется выносливостью материала.

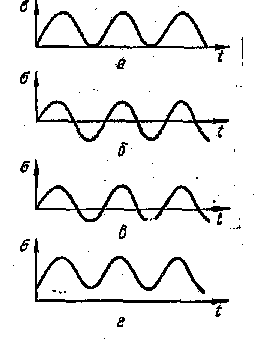
Рис. 89 Усталостное разрушение наблюдается при наличии одной из сле­дующих особенностей нагружения:

1)при многократном нагружении одного знака, например, периодически изменяющегося от нуля до максимума (рис.89, а);

2)при многократном нагружении, периодически изменяющемся не только по величине, но и по знаку (знакопеременное нагруженне), когда на выносливость материала одновременно оказывает влияние и повторность, и переменность нагружения. При этом различают симметрич-ное нагружение (рис.89, б) и несимметричнее (рис.89, в, г). В связи с этим различают симметричный цикл(рис.89 а) и множество несимметричных(рис.89б,в,г) Несимметричные делятся на двусторонние(рис.89 в), односторонние положительные (рис.89 г)и односторонние отрицательные, и отнулевые (или пульсирующие) положительные (рис.89 а) и отрицательные.

Для разрушения от усталости недостаточно переменности напря­жений. Необходимо также, чтобы напряжения имели определенную величину. Максимальное напряжение, при котором материал способен сопротивляться, не разрушаясь, при любом произвольно большом числе повторений нагружений, называется пределом выносливости.

Усталостный излом металла имеет характерный вид. На нем обычно можно наблюдать две зоны: одна (А) гладкая, притертая, образованная вследствие постепенного развития трещин. Другая (В) крупнозернистая, образованная при окончательном изломе ослабленного развившейся усталостной трещиной сечения детали. Зона В у хрупких материалов имеет крупнокристал-лическое, а у вяз­ких — волокнистое строение.

Механизм образования трещин при повторно-переменном напря­жении весьма сложен и не может считаться полностью изученным. Из несомненных положений теории усталости можно отметить следующие: а)процессы, происходящие в материале при повторно-переменном загружении носят резко выраженный местный характер;

б) решающее влияние на явление усталости до образования первой трещины оказывают касательные напряжения, вызывающие пластические сдвиги и разрушение путем среза. Развитие усталостных трещин ускоряется при наличии растягивающих напряжений и у пластичных, и в особенности у хрупких материалов (типа чугуна), у которых появление

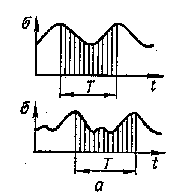
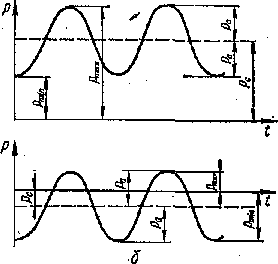
Рис.90

трещин отрыва значительно повышает чувствительность к растягивающим напряжениям.

Предел выносливости определяется экспериментально на соответ­ствующих испытательных машинах путем испытания партии образцов из данного материала в количестве не менее 6—12 штук. Предел вы­носливости зависит от многих факторов, в том числе от формы и размера образца или детали, способа ее обработки, состояния поверхно­сти, вида напряженного состояния (растяжение сжатие, кручение, изгиб), закона изменения нагрузки во времени, темпе­ратуры и т. п.

В большинстве случаев переменные напряжения, (которые могут быть и нормальными и касательными) вызывающие разрушение от усталости, представляют собой функцию времени с периодом, равным Т. Совокупность всех значений напря­жений за один период, называется циклом напряжений (рис.90 , а). На величину предела выносливости оказывают влияние максимальные (р_мах) и минимальные (р_мин) напряжения цикла.

Основной характерис­тикой цикла является коэффициент асимметрии цикла R =

Различают также среднее напряжение цикла Р_с = и амплитуду цикла Р_а = 𝗅

Среднее напряжение цикла может быть как положительным, так и отрицательным; амплитуда цикла определяется абсолютной величи­ной (без учета знака).

Очевидно, что р_мах = Р_с + Р_а р_мин = Р_с - Р_а

Наиболее опасным циклом является так называемый симметричный (когда Р_мах = —Р_мин и р_с = 0), при котором R = = - 1 Предел выносливости при симметричном цикле обозначается как р_-1

При пульсирующем цикле, когда р_мин = О; R = предел выносливости обозначают через р₀

Циклы, имеющие оди­наковые характеристики R, называют подобными. Характеристика цикла, или коэффициент асимметрии, может изменяться от — ∞ до + ∞

Следует иметь в виду, что в случаях, когда речь идет об усталости при растяжении — сжатии или изгибе, вместо обозначений р_а, р_с, р_в, р_мах, р_мин и т. д. необходимо использовать обозначения соответственно σ_а , σ_с , σ_мах , σ_мин , а в случае рассмотрения сопротивления материалов действию повторно-переменных касательных напряжений (при циклическом кручении) следует применять обозначения τ_а, τ_с, τ_мах, и т. д.

Методы определения предела выносливости. Диаграммы усталости.

При испытании материала на выносливость чаще всего используют гладкие цилиндрические образцы диаметром 7—10 мм. В зависимости от типа действующих в образце повторно-перемен­ных напряжений (растяжения — сжатия, переменного изгиба, переменного, кручения), а также характеристики цикла (коэффициент асимметрии R ), значения предела выносливости будут различным. Поэтому, ставя перед собой цель получения предела выносливости материала, следует заранее указать, при каком виде деформации (изгибе, кручении и т. п.), а .также при каком характере изменения напряже­ний за цикл, т. е. при каком значении R, требуется определить предел выносливости.

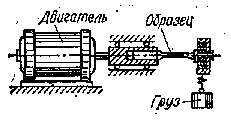
рис.91 В соответствии с поставленной задачей выбирают испытательную машину. Для испытания на усталость при изгибе применяют машины, в которых циклические симметричные напряжения в испытываемом образце возникают за счет вращения образца, нагруженного укрепленным на конце с помощью шарикового подшипника грузом (рис.91). Число оборотов в минуту таких машин обычно составляет около 3000 (50 Гц). Для испытаний используются также ма­шины с другим типом привода с диапазоном частот от 5 до 20000 Гц. Испытания проводятся при симметричном и асимметричном цик­лах нагружения в основном при изгибе или при растяжении — сжатии образцов. При испытании партии образцов с целью определения предела вы­носливости необходимо обеспечивать в отдельных образцах

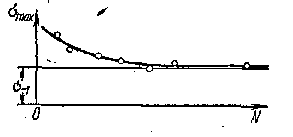
Рис.92

различные напряжения для выявления закономерности изменения числа циклов до разрушения при тех или иных уровнях напряжений.

Обработка получаемых экспериментальных данных осуществляется путем построения кривых усталости, часто называемых кривыми Веллера (рис.92 ).

Кривая усталости строится по точкам в координатах: максимальное напряжение цикла р_мах (σ_мах или τ_мах) — число циклов до разрушения N, каждой точке соответствует один разрушившийся образец, прора­ботавший N циклов с заданным р_мах

По мере снижения напряжения образцы выдерживают до разру­шения все большее число циклов, а кривая усталости приближается к некоторой асимптоте, параллельной оси абс­цисс N. Число циклов, при котором кривая усталости практически начинает совпадать с асимптотой, может быть принято за базу испыта­ния на выносливость, т. е. за такое число циклов, превышение которого при данном напряжении практически не должно приводить к разру­шению образца. Таким образом, базой испытания на выносливость на­зывается наибольшее число повторно-переменных нагружений, существенное превышение которого не должно приводить к усталостным разру­шениям испытываемого образца при данном напряжении. Для черных материалов (сталь, чугун и т. п.) в инженерной прак­тике за базу испытания принимают 10 млн. циклов; для цветных (медь, алюминий и т. п.) — база испытания берется в 5— 10 раз боль­ше, чем для черных металлов.

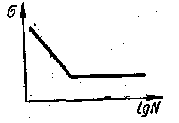В некоторых случаях, особенно для цветных материалов, кривая усталости в координатах N, р медленно стремится к асимптоте, по­этому базу испытания приходится выбирать значительно большей. В таких случаях вообще трудно говорить об истинном, так называемом физическом пределе выносливости, поскольку таковой практически отсутствует. Говорят об условном пределе выносливости, понимая под ним максимальное напряжение, при котором не происходит разрушения при осуществлении определенного наперед заданного числа циклов, принимаемого за базу испытания.

Рис.93 Кроме построения первичных диаграмм уста­лости в координатах N, р при растяжения — сжатии и изгибе или в координатах N, τ_мах при кручении, эти диаграммы строят также в полу­логарифмических координатах lgN, σ_mах (рис.93 ). В этом случае предел выносливости будет характеризоваться ординатой горизонтального прямого участка кривой усталости.

Как показывают многочисленные испытания на усталость, для не­которых материалов можно заметить следующие соотношения между пределами выносливости при симметричном цикле, полученными при изгибе ; кручении ; и растяжении — сжатии на гладких образ­цах. Для стали = 0,7 ; для чугуна = 0,65 ; = 0,8 для сталей и легких сплавов = 0,55

Замечено также, что для стали существуют следующие соотношения указанных пределов вынос­ливости с временным сопротивлением при растяжений: = 0,2 ; = 0,4 = 0,22 . Для цветных металлов = (0,24—0,50)

Диаграмма предельных напряжений.

Для характеристики сопро­тивляемости материала повторно-переменным напряжениям при раз­личной асимметрии цикла строится так называемая диаграмма предель­ных напряжений (рис. 94 ) в координатах σ_мах, σ_мин — σ_с (диаграмма Смита).

Ординаты кривой САВ диаграммы соответствуют значениям пре­делов выносливости (максимальным значениям напряжения) при раз­личной асимметрии циклов, которые берутся из первичных диаграмм усталости.

Тангенс угла наклона луча, проведенного из начала координат до пересечения с предельной кривой САВ и образующего угол β с осью абсцисс σ_с , будет = = Ординаты луча под углом β = 45° определяют среднее напряжение цикла σ_с.

Диаграммы предельных напряжений обычно ограничивают в верх­ней части пределом прочности или пределом текучести материала. Примерный вид диаграммы предельных напряжений, ограниченной пределом текучести, для случая циклического кручения приведен на рис.95 .

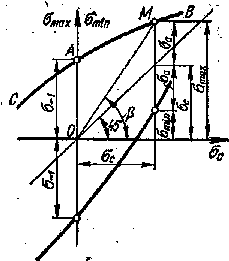
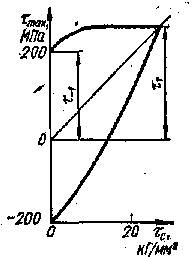
Рис. 94 (диаграмма Смита) Рис.95

Можно строить также диаграмму предельных амплитуд напряже­ний в координатах σ_а — σ_с (диаграмма Хейя). В этом случае (рис.96) тангенс угла образованного лучом, проведенным из начала координат, с предельной кривой будет выражаться так: = =

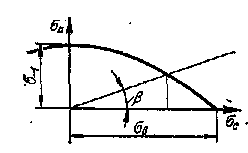
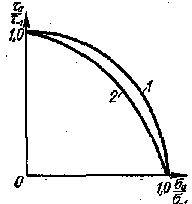
Рис.96 (диаграмма Хейя) Рис.97

Для оценки сопротивляемости материалов повторно-переменным напряжениям при сложном напряженном состоянии, например при совместном действии циклического изгиба и кручения, используют со­ответствующие усталостные машины, позволяющие получать интере­сующее нас напряженное состояние. На рис.97 приведены результаты экспериментов с гладкими об­разцами при различном сочетании переменных нормальных (σ) и ка­сательных (τ) напряжений при симметричном цикле. Через и обозначены пределы выносливости соответственно только при изгибе и только при кручении, а через σ_а и τ_а — предельные амплитуды при одновременном действии изгиба и кручения. Экспериментальные дан­ные группируются около кривой, которая с достаточной степенью точности может быть аппроксимирована для конструкционных сталей ду­гой круга (рис.97 , кривая 1) Для высокопрочных сталей и чугунов экспериментальные данные располагаются ближе к эллиптическим дугам (рис.97 , кривая 2).

В случае симметричного цикла с соблюдением синхронности и синфазности напряжений условие прочности в амплитудах главных на­пряжений в соответствии с третьей теорией прочности запишется так: (σ₁)_а – (σ₃)_а = а по четвертой теории прочности + + = 2

При сложном напряженном состоянии, характеризуемом совместным действием циклического изгиба и кручения, условие прочности с учетом соотношения будет иметь вид =

Влияние на предел выносливости конструктивно-технологических факторов

Влияние концентрации напряжений. Равномерное распределение напряжений по площади поперечного сечения стержня имеет место только в тех случаях, когда поперечные сечения по длине стержня постоянны или изменяются плавно. Наличие резких изменений площади поперечного сечения вследствие резких переходов, отверстий, выточек, надрезов и т, д, приводит к неравномерному распределению напряжений и к увеличению их в отдельных местах сечения. Это явление называется концентрацией на­пряжений.

На рисунке 98,а показана эпюра рас­тягивающих напряжений в сечении полосы с круглым отверстием малого диаметра, а на рис.98,б —эпюра напряжений в сечении полосы с боковыми выточками. Причины, вызывающие концентрацию напряжений (отверстия, выточки, царапины и т. д.), называются концентраторами напряжений. Максимальной величины на­пряжения достигают вблизи концентратора (у края отверстия и т, д.) и носят мест­ный характер. Поэтому напряжения в местах концентрации называются местными.

Номинальным называется напряжение, вычисленное в ослабленном сечении без учета концентрации. Например, в стержне рис.98,а номинальное напряжение определяется как среднее, в ослабленном сечении. N — усилие в сечении; А_о— площадь ослабленного сечения, обычно называемая площадью нетто. σ_н =

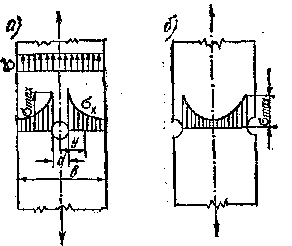
Рис. 98 Количественной характеристикой концентрации напряжений является коэф­фициент концентра-ции, равный отношению наибольшего местного напряжения (σ_мах) к номинальному (σ_н) 𝛼 = Наибольшее влияние на предел выносливости оказывает концентрация напряжений, степень которой характеризуется теоретическим коэффициентом концентра­ции. Как показывают опыты, предел выносливости об­разцов с концентраторами напряжений р_—1К оказывается больше вы­численного через теоретический коэффициент концентрации 𝛼, т. е. р_—1К≥

Поэтому наряду с теоретическим коэффициентом концентрации 𝛼 для циклического нагружения введе­но понятие эффективного, или действительного, коэффициента кон­центрации k. Эти коэффициенты обозначены так: для нормальных напряжений k_σ = для касательных напряжений k_τ =

где и — пределы выносливости, полученные при действии цик­лических нормальных и касательных напряжений на гладких образ­цах; и — пределы выносливости образцов с концентраторами напряжений.

Практически оказалось удобнее определять эффективный коэффициент концентрации через так называемый коэффициент чувствительности материала к концентрации напряжений. q =

Коэффициент чувствительности материала к концентрации напряжений зависит от самого материала и величины коэффициента концен­трации 𝛼. Ниже приведены ориентировочные значения коэффициента для различных материалов.

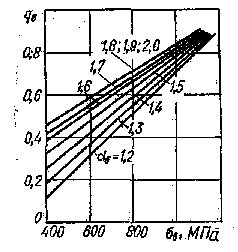
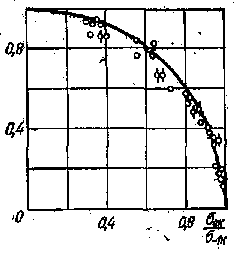
Рис.99 Рис.100

0.2 0,1-0,4 0,3—0,5 0,4—0,6 0,6—0,7 0,7—0,9

Материалы

Литые материалы и материалы с внутренними источниками концентрации и дефектами (серый чугун и др.)

Литые жаропрочные сплавы, стальное и алюминиевое литье, модифицированные чугуны

Низкоуглеродистые стали, жаропрочные деформируемые спла­вы, аустенитные коррозионностойкие стали, алюминиевые деформируемые сплавы

Среднеуглеродистые стали, низколегированные стали

Конструкционные легированные стали

Высоколегированные стали (типа коррозионностойких сталей мартенситного класса), титановые сплавы

Для определения коэффициента чувствительности имеются графики (рис.99 ). Зная q, а также теоретический коэффи­циент концентрации напряжения 𝛼, можно определить эффективный коэффициент концентрации по формуле k =1 + q(𝛼 – 1)

Для материала, чувствительного к концентрации напряжения, когда q→1 то k → 𝛼. Для материала, не чувствительного к концентра­ции напряжения, когда q→0 то k → 1.

Влияние концентрации напряжений при сложном напряженном состоянии оценивается на основе испытания образцов с концентраторами и получения соответствующих диаграмм (рис. 100), которые аналогично диаграммам, приведенным для гладких образцов (рис.97), описываются эллиптической зависимостью.

где σ_-1к, τ_-1к — пределы выносливости при симметричном цикле для образцов с концентраторами только при изгибе и только при кручении соответственно; σ_ак, τ_ак —амплитудные значения напряжений при одно­временном синхронном и синфазном, изменении напряжений, при слож­ном напряженном состоянии и различных сочетаниях переменных нор­мальных и касательных напряжений.

Влияние размеров (масштабный фактор). Эксперименты показы­вают, что с увеличением размеров образца предел выносливости падает. Это снижение обычно учитывал­ся с помощью некоторого коэф­фициента, обозначаемого, напри­мер, применительно к нормаль­ным напряжениям так

Где — предел выносливости гладкого лабораторного образца диаметром = 7 – 10 мм предел выносливости рассматриваемой детали диаметром d > . Коэффициент влияния абсолют­ных размеров < 1.

При наличии концентратора влияние масштаба оценивается так же, как и для гладких образцов, с помощью коэффициента

Здесь и — пределы выносливости детали и лаборатор­ного образца соответственно.

На рис. 101 приведены кривые зависимо­сти ε =f(d). Здесь кривая 1 соответствует детали из углеродистой ста­ли без концентратора; кривая 2 — детали из легированной стали (σв = 1000— 1200 МПа) при отсутствии концентратора и из углеродистой стали при наличии концентратора; кривая 3 соответствует детали из легированной стали при наличии концентратора; кривая 4 — для лю­бой стали при весьма большой концентрации напряжений (например, при концентраторе типа надреза).

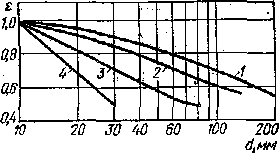
Рис.101 Снижение предела выносливости с увеличением размеров особенно сильно выражено у неоднородных материалов. Так, с увеличением размера образца из серого чугуна с 5—10 мм до 50 мм снижение может достигнуть 60—70 %. Для углеродистой стали увеличение диаметра образца с 7 мм до 150 мм приводит к снижению предела выносливости примерно на 45 %.

Кроме эффективного коэффициента концентраций для образ­ца вводят понятие эффективного коэффициента концентрации напряжений для детали , учитывающего

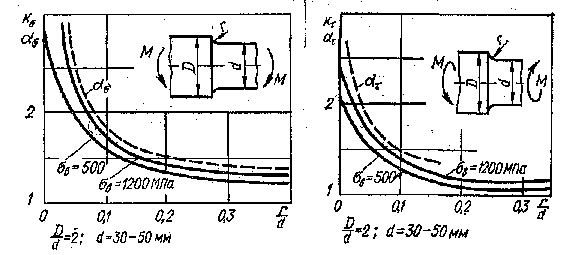
Рис.102 Рис.103

одновременно и размеры и концентрацию: =

Если определяется на образцах достаточно большого диаметра (когда дальнейшее увеличение диаметра мало влияет на , то = =

В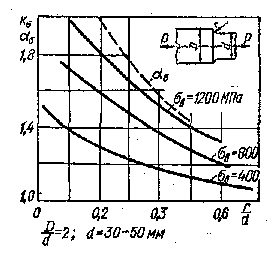 лияние концентраторов напряжения существенно зависит от вида напряженного состояния. При циклическом кручении, например, коэффициент оказывается более низким, чем при изгибе при той же форме концентратора. На рис.102 и рис.103 приведены значения эффективных коэффициентов концентрации для ступенчатых валов с галтелью соответственно для изгиба и кручения. Соотношение между k_τ и k_σ может быть выражено формулой k_τ= 1 + 0,6 (k_σ – 1)

Рис.104

На рис. 104 приведены графики, характеризующие эффективные коэффициенты концентрации при растяжении — сжатии. Из. графиков (рис. 102 и 104) видно, что значения эффективных коэффициентов при растяжении — сжатии несколько превышают таковые при изгибе.

Влияние состояний поверхности На предел выносливости суще­ственное влияние оказывает состояние поверхности детали или образ­ца. Это объясняется тем, что на поверхности почти всегда имеют место дефекты, связанные с качеством ее механической обработки, а также с коррозией под влиянием окружающей среды. Поэтому усталостные трещины, как правило, начинаются с поверхности, а плохое качество последней приводит к снижению предела выносливости.

Влияние качества механической обработки поверхности на вынос­ливость можно оценить некоторым коэффициентом 𝛽 < 1, который равен отношению предела выносливости испытуемого образца с опре­деленной обработкой поверхности к пределу выносливости тщательно отполированного образца. На рис. 104 приведена зависимость коэффи­циента 𝛽 от предела прочности для различных видов обработки по­верхности стальных образцов. Кривая 1 соответствует полированным образцам; 2 — шлифованным; 3 — образцам с тонкой обточкой; 4 — образцам с грубой обточкой; 5 — с наличием окалины. Из графика видно, что при грубой обточке предел выносливости снижается на 40 %, а при наличии окалины — на 70 %.

Рис.105 Рис.106

Влияние коррозии на величину предела выносливости при ротационном изгибе показано на рис.106 , где по оси ординат отложено значение коэффициента 𝛽_кор = , а по оси абсцисс временное сопротивление материала исследуемых образцов. Кривая 1 характеризует влияние коррозии в пресной воде при наличии концентраторов; Кривая 2 характеризует влияние коррозии в морской воде при наличии концентраторов и в пресной при отсутствии концентраторов; Кривая 3 характеризует влияние коррозии в морской воде при отсутствии концентраторов;

Влияние пауз. На предел выносливости имеют влияние паузы (перерывы нагружения). Иногда за счет пауз число циклов до разруше­ния увеличивается на 15 — 20 %. Увеличение числа циклов тем больше, чем чаще паузы и чем они длительнее (последний фактор влияет слабее).

Влияние перегрузок (нагрузок, больших предела выносливости) на величину предела выносливости зависит от характера перегрузок. При малых перегрузках до определенного числа циклов сопротивление усталостному разрушению повышается, при больших перегрузках после определенного числа циклов — понижается.

Влияние тренировки. Если создавать в образце напряжения не­много ниже предела выносливости, а затем постепенно их увеличивать, то сопротивление усталости материала может быть существенно повы­шено. Это явление, называемое тренировкой материала, широко используется в технике. Особого эффекта можно достигнуть при постепенном увеличении перегрузки. При этом упрочнение можно получить при сравнительно кратковременных тренировках (порядка 50 000 цик­лов), но при сильных перегрузках.

Влияние температуры. Применительно к обычным конструкцион­ным материалам повышение температуры приводит к снижению пре­дела выносливости, а снижение температуры — к повышению предела выносливости как гладких образцов, так и образцов с концентраторами.

Для стали при температурах выше 573К с повышением на каж­дые 100 К предел выносливости падает на 15—20 %. Однако для некоторых сталей с повышением температуры от 293 до 673 К на­блюдается некоторое повышение предела выносливости. Это повышение, по-видимому, связано с физико-химическими процессами, протекающими в материале под одновременным воздействием температуры и цик­лических напряжений. Влияние концентрации напряжений на вынос­ливость, как правило, с повышением температуры уменьшается.

При понижении температуры от 293 до 83 предел выносливости у некоторых сталей увеличивается более чем вдвое, хотя ударная вязкость при этом существенно падает.

Расчет на прочность при повторно-переменных нагрузках При простых видах деформации детали, работающей при симмет­ричном цикле, например, при циклическом растяжении — сжатии или изгибе и фактически действующем знакопеременном напряжении σ_а , запас прочности можно определить по формуле = где — предел выносливости детали при растяжении—сжатии или изгибе, который может быть определен по пределу выносливости лабораторных полированных образцов с учетом эффективного коэффициента концентрации , масштабного фактора , состояния поверхности и среды, характеризуемых соответственно коэффициентами 𝛽 и 𝛽к , по формуле = В случае сложного напряженного состояния = или Тогда, учитывая, что коэффициенты запаса прочности = и = получаем откуда запас прочности при сложном напряженном состоянии определяется формулой n = В случае определения запаса проч­ности при асимметричном цикле и любом виде циклического нагружения (изгиб, растяжение — сжатие, кручение) можно всходить из схематизированной диа­граммы предельных напряжений для гладких образцов (рис. 107), предста­вив ее в виде прямой, проходящей через точки А и В с координатами 0 , и уравнение которой имеет вид = + = + Или = + где = коэффициент чувствительности материала к асимметрии цикла. Аналогично, при действии касательных напряжений = + Значения и для сталей с различным временным сопротивлением приведены ниже

σв , МПа	Ψσ	Ψτ
350-550	0	0
520-750	0.05	0
700- 1000	0.1	0.05
1000- 1200	0.2	0.1
1200- 1400	0.25	0.15

П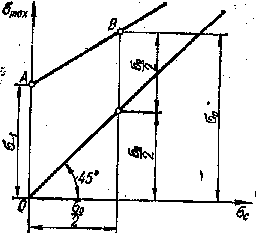 редельная амплитуда напряжений для гладкого образца на ос­новании может быть выражена формулой

Рис.107

Предельная амплитуда напряжений для детали = = а уравнение кривой предельных напряжений для детали (рис.107 ) может быть записано в виде = + = +

Для определения запаса прочности детали, напряжение в которой на диаграмме предельных напряжений (рис.108) характеризуется точкой М с координатами σ_а , σ_с, необходимо найти координаты точки N, находящейся на пересечении луча, выходящего из начала координат, с кривой предельных напряжений для детали. Координаты точки N определятся из совместного рассмотрения уравнений кривой (линии) предельных напряжений для детали = + и уравнения луча = · где штрихами обозначены текущие координаты. Ордината точки N, лежащей на пересечении прямых АМ и ОN будет одна и та же, т. е. = или + =

откуда находим абсциссу точки N = Учитывая, что получим =

Обозначим ординату как и подставим в уравнение луча =

Таким образом, окончательное выражение для запаса прочности запишется так: = =

Аналогично при кручении =

При сложном сопротивлении и несимметричном цикле запас прочности может быть определен по формуле n =

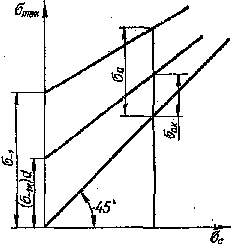
Рис.108 Рис. 109

Выбор запаса прочности при расчетах на действие повторно-пере­менных напряжений зависит от точности определения усилий и напря­жений, от однородности материала, качества обработки детали и дру­гих факторов. При повышенной точности определения напряжений (в частности, с использованием тензометрирования), однородном ма­териале и качественной обработке принимают запас прочности n = 1,3- 1,4. Для обычной точности определения усилий и умеренной однород­ности материала n= 1,44 — 1,7. При пониженной точности определе­ния усилий и напряжений, а также пониженной однородности материа­ла n = 1,7 — 3,0.

Остановимся на порядке проектировочного расчета на выносливость, например, штока поршневого двигателя, когда даны нагрузка, действу­ющие на проектируемую деталь (p_max и p_min); задан материал, т. е. известны σ_в, σ_т, ,известна технология обработки детали; изве­стен тип концентратора (предположим, задан диаметр поперечного отвер­стия в детали δ) и требуется определить размеры детали. При решении поставленной задачи, прежде всего, устанавливают опасное сечение детали, которым, очевидно, будет сечение в месте концентратора. Так как соот­ношения диаметра отверстия концентратора и диаметра самой детали не­известны, следует задаться теоретическим коэффициентом концентрации и для данного материала по известному (σ_в) из графика (рис.99) при данном определить коэффициент чувствительности материала к концентрации напряжений , а затем по формуле = 1+ ( -1) найти значение эффективного коэффициента концентрации. Из графи­ка (рис. 105) находят значение коэффициента 𝛽, характеризующего качество обработки поверхности. Задавшись коэффициентом ε , учиты­вающим размеры, определяют эффективный коэффициент концентрации детали = Затем, задавшись коэффициентом запаса прочности , по формуле = = = находим площадь поперечного сечения детали А =

И ее диаметр d =

По окончании расчета необходимо проверить правильность выб­ранного коэффициента ε по графику (рис.101 ) при известном теперь диаметре детали d. В случае резкого расхождения полученного значе­ния в с принятым ранее расчет необходимо уточнить.

В случае проверочного расчета, известны форма и размеры детали (предположим, речь идет о круглом ступенчатом стержне, подвержен­ном осевой повторно-переменной нагрузке с заданной асимметрией цикла); заданы максимальный диаметр d и радиус закругления r в мес­те сопряжения разных диаметров вала; известен материал детали (σ_в, σ_т, ) и качество ее механической обработки. Требуется опреде­лить допускаемое усилие, которое может выдержать деталь. Решать поставленную задачу следует в таком порядке.

1. Установить теоретический коэффициент концентрации поль­зуясь, например, графиком, приведенным на рис. 104. 2. По графику (рис. 99) найти коэффициент чувствительности к концентрации напряжений 3. Определить эффективный коэффициент концентрации = 1+ ( - 1) 4. По графику (рис.101) найти коэффициент влияния абсолютных размеров ε 4. По графику (рис.105) найти коэффициент 𝛽, учитывающий качество обработки поверхности. 6. Найти эффективный коэффициент концентрации напряжений для детали = 7. Задаться коэффициентом запаса прочности 8. Определить амплитуду напряжений, исходя из формулы = откуда σ_а =

Обычно для некачественных сталей 0, тогда σ_а =

9. Определить допускаемое амплитудное усилие р_а = А_мин· σ_а =

10. Найти среднее усилие р_с = р_а

11. Определить максимальное и минимальное усилие цикла p_max= р_а+ р_с и p_min = p_maxR

Рассмотрим порядок определения запаса прочности для вращающегося круглого трубчатого вала с поперечным отверстием для смазки δ, испытывающего переменный изгиб при симметричном цикле с заданным М_mах = М_а совместно с переменным кручением с М_{кр mах} при известной асимметрии цикла R. Известен наружный D и внутрен­ний d диаметры вала, материал вала (σ_в, σ_т, ), а также качество механической обработки поверхности вала.

Задачу следует решать в таком порядке.

1. Определить номинальные напряжения в вале от изгиба и кру­чения

= ; σ_а = ; = 0 ; = ; τ_min = ; = ; =

2. Определить коэффициент концентрации при изгибе при известном δ /D (рис. 111).

3. Определить по графику (Рис.99) при найденном и известном σ_в коэффициент чувствительности к концентрации напряжений , и найти эффективный коэффициент концентрации при изгибе = 1 + ( - 1)

4. Выбрав по графику (рис. 101) ε, а по графику (рис. 105) — 𝛽 определить эффективный коэффициент концентрации для детали =

5. Определить запас прочности при изгибе по формуле = = (так как для рассматриваемого случая = 0).

6. Установить коэффициент концентрации при кручении , а также, приняв , определить эффективный коэффициент концентрации при кручении = 1 + ( - 1)

Приняв те же значения ε и 𝛽 , что и при изгибе, найти эффектив­ный коэффициент концентрации для детали при кручении =

7. Определить запас прочности при кручении =

8. Вычислить общий коэффициент запаса прочности n =

Понятие о малоцикловой усталости материалов

Во многих реальных инженерных конструкциях наблюдается раз­рушение после относительно небольшого числа циклов нагружения, выражаемого несколькими тысячами. При этом в материале могут про­исходить явления, типичные для усталости (возникновение и разви­тие трещины). Поэтому разрушение материала при сравнительно не­большом числе циклов нагружения (10² — 10⁵) называют малоцикловой усталостью. Это является определенным упрощением, так как для кон­струкционных пластичных материалов при числе циклов до 10³—2·10⁴ может иметь место квазистатическое разрушение. Разруше­ние от малоцикловой усталости обычно происходит при значительной (около 1 %) пластической циклической деформации в макрообъемах рассматриваемого элемента конструкции. Расчеты элементов конструкций на малоцикловую усталость ба­зируются на экспериментальных данных изучения закономерностей сопротивления деформированию и разрушению при циклическом упру­го-пластическом деформировании, а также исследованиях кинетики неоднородного напряженно-деформированного состояния и накопле­ния повреждений в зонах концентрации — местах вероятного разру­шения. Сопротивление материалов циклическому упруго-пластическому деформированию обычно изучают при однородном напряженном со­стоянии, используя два основных вида нагружения: мягкое — при по­стоянной амплитуде напряжений и жесткое — при постоянной амп­литуде деформации.

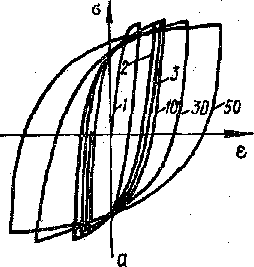
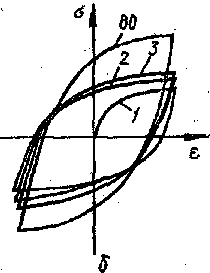
Рис.110 Рис.111

Процесс упруго-пластического деформирования при малоцикло­вом нагружении исследуется обычно путем построения петель гисте­резиса в координатах напряжение—деформация Схематическое пред­ставление таких петель для указанных основных видов нагружения приведено на рис. 110 (а — мягкое нагружение, Ь — жесткое нагружение), где цифры указывают на номера циклов нагружения.