Свободные колебания системы с одной степенью свободы с учетом сопротивления, пропорционального скорости

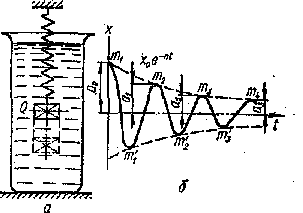
Рис. 87

Уравнение свободных колебаний системы с одной степенью сво­боды (рис.87, а) с учетом сопротивления, пропорционального скоро­сти движения колеблющегося груза, получим из рассмотрения усло­вий его динамического равновесия: Q - ẍ - αẋ = Q + cx

Или ẍ + 2 n ẋ + = 0 В этом уравнении = ; 2 n = ; α— коэффициент пропорциональности; αх — сила сопротивле­ния. Обозначим =

Решение уравнения будет x = (A + B ) где е = 2,718.

Период затухающих колебаний рассматриваемой системы Т = =

где n — коэффициент, характеризующий демпфирующую способность колебательной системы. Из решения видно, что из-за множителя амплитуда колебаний с течением времени уменьшается — колебания затухают. Постоянные интегрирования А и В в решении определяются из начальных условий. Так, полагая, что при t = 0 х = х₀ ẋ = , находим B = х₀ A = ( + n х₀ )

В этом случае решение может быть представлено в виде: x = В частном случае, когда А = 0, т. е. когда + = 0 Уравнение примет вид x =

Графически это уравнение представлено на рис. 87, б. Уменьшение амплитуды следует геометрической прогрессии. Действительно, при t = 0 ; T ; 2T амплитуды соответственно имеют значения = х₀ ; = ; = а отношения двух, рядом расположенных амплитуд = = = ··· = =

Откуда = = nT = δ

Величина δ называется логарифмическим декрементом колебаний и обычно является основной характеристикой затухания колебаний; или характеристикой демпфирующих свойств колебательной системы.

Демпфирующая способность материала

Среди различных причин, обусловливающих гашение колебаний механических систем, особый интерес представляет естественное по­глощение энергии колебаний в материале упругих элементов самой ко­лебательной системы. Любой реальный материал способен при его циклическом деформировании в большей или меньшей степени погло­щать энергию циклического деформирования, преобразуя ее в тепло­ту, которая затем рассеивается.

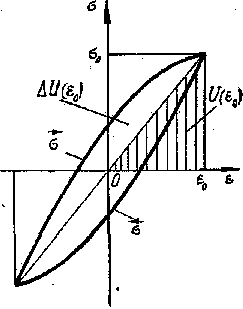
Рис. 88

Способность материала необратимо поглощать механическую энер­гию обусловлена его несовершенной упругостью, проявляющейся в не­линейности и неоднозначности зависимостей между напряжением и де­формацией при нагружении и разгрузке и приводящей к образованию петли гистерезиса (рис.84), площадью которой характеризуется величина по­глощенной (или рассеянной) в единице объема материала энергии за цикл его деформирования с данной амп­литудой деформации (напряжения).

В общем случае симметричного цик­ла деформирования уравнения восходя­щей и нисходящей ветвей петли гистерезиса, обусловленного несовер­шенной упругостью стабильного состоя­ния материала, можно представить в виде σ_e= E

где n, х_n— параметры петли гистерези­са, подлежащие определению.

Отмеченная, способность материала начинает проявляться при амп­литудах напряжений, значительно меньших макроскопического пре­дела упругости, и для области рабочих амплитуд деформаций деталей инженерных конструкций в основном обусловливается микропласти­ческими деформациями, связанными с перемещениями дислокаций, перемещениями межфазных границ и границ двойников, связанными с наличием обратимого мартенсита в структуре, а также магнито-механическим гистерезисом, связанным с необратимыми смещениями границ доменов.

Применительно к инженерным задачам гашения (демпфирования) колебаний элементов конструкций рассматриваемая способность мате­риала поглощать энергию его циклического деформирования называет­ся демпфирующей способностью.

Эта способность материала как один из основных факторов, обус­ловливающих ограничение амплитуды резонансных колебаний и зату­хание свободных колебаний и влияющих на динамическую устойчи­вость и развитие автоколебаний, имеет важное значение для обеспече­ния не только динамической прочности вибрирующих элементов, но и устойчивой работы аппаратуры, а также улучшения комфортабель­ности транспортных машин н повышения эффективности работы виб­рационных машин резонансного типа. При этом, если обычно стремят­ся обеспечить максимальное демпфирование колебаний упругого эле­мента, что считается одним из условий оптимального конструирования, то, например, для резонансной системы вибрационной машины желательно иметь минимальный уровень демпфирования.

Демпфирующая способность материала обычно характеризуется относительным рассеянием энергии Ψ( ) =

где ) — амплитудное значение энергии упругого деформирова­ния (площадь заштрихованного на рис. 88 треугольника), или лога­рифмическим декрементом колебаний .

Демпфирующая способность конструкционных материалов зави­сит от многих факторов; химического состава и структуры материала, амплитуды циклической деформации (напряжения) и вида напряженного состояния, температуры и термической об­работки , статической напряженности и внешнего магнитного поля , предварительного пластического дефор­мирования и длительности воздействия циклического деформирования и др. Демпфирующая способность рассматривается как самостоятель­ная характеристика материала, требующая в основном эксперимен­тального определения с учетом реальных технологических и эксплу­атационных факторов.

Известные конструкционные материалы различаются по демпфи­рующей способности весьма существенно — на три порядка. Ниже приведены некоторые ориентировочные данные о максимальном зна­чении декремента колебаний различных классов материалов при ампли­туде гомологического напряжения, равного примерно одной десятой предела текучести данного материала, в условиях комнатной температуры

материал	δмах %	материал	δмах %
сплавы алюминиевые	0.1-1	Чугуны с графитом пластинчатым	10-15
магниевые(литые)	13-30	Чугуны с графитом шаровиднымым	2-5
марганцевомедные	10-25	стали хромистые	1-4
Медноалюминиевые*	4-10	стали углеродистые	0.2-1
никельтитановые	10-15	латуни и бронзы	0.1-0.3
кобальтоникелевые	6-12
титановые **	0,05 - 0,15

* Сплавы с обратимым мартенситом в структуре.

** Для сплавов с обратимым мартенситом в структуре возможно повышение демпфирующей способности на порядок и более.

Следует отметить, что результаты имеющихся исследований позволяют считать для области амплитуд циклических напряжений, не пре­вышающих предела выносливости, демпфирующую способность метал­лических материалов независимой от частоты деформирования.