Свободные колебания систем с одной степенью свободы

Простейшей колебательной системой с одной степенью свободы может служить груз, подвешенный на вертикально расположенной пружине (рис.84 ).

Дифференциальное уравнение колебаний груза Q получим, взяв сумму проекций всех сил (включая силы инерции согласно принципу Даламбера) на вертикальную ось, в виде

Q + cx – (Q - ẍ) = О

Отсюда ẍ + cx = О или ẍ + ω² = 0

где х — вертикальное перемещение груза от поло­жения статического равновесия; ẍ = ; t — время; с — жесткость пружины; — ускорение свободного падения; ω — угловая частота свободных колебаний ; ω² = =

Общий интеграл дифференциального уравнения второй степени имеет вид:

x = А + В

где A и В — постоянные интегрирования, зависящие от начальных условий.

Если заданы начальная координата груза х₀ и начальная скорость v_o= ẋ при t = 0, то из общего интеграла определим А = х_о ; В = ;

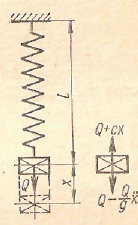
Рис. 84

Полагая Х_о = а· ; = а· решение можно представить в виде х = а· где а – амплитуда колебаний, определяемая по формуле а = =

угловая частота колебания (число колебаний, совершаемое в течение 2π секунд) получается = или = где m = — масса подвешенного груза.

Зная, угловую частоту, можно определить период колебаний T = = 2π = 2π

Техническая частота (число колебаний в секунду, гц) определится формулой f = =

При колебаниях груза, подвешенного на конце пружины, представляющей собой стержень длиной ℓ с жесткостью поперечного сечения на растяжение ЕА и жесткостью с =

собственная частота колебаний опре­делится формулой = =

Учитывая, что m = можно записать и в таком виде = =

Из полученных формул видно, что частота сво­бодных колебаний системы при неизменной массе возрастает с увеличением жесткости и уменьшается с увеличением массы при неизменной жесткости. Отношение частот свободных колебаний грузов, прикрепленных к концам двух разных стержней, обратно пропорци­онально корню квадратному из отношения статических удлинений стержней.

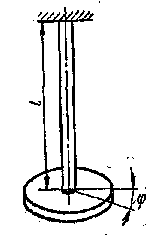
Примером системы с одной степенью свободы может служить так­же колебательная система, состоящая из массивного диска, прикреп­ленного к нижнему концу жестко закрепленного верхним концом вала (рис.85 ). Если к диску в его плоскости приложить и внезапно уда­лить пару сил, то возникнут свободные колебания кручения вала вместе с диском. Обозначим крутильную жесткость вала (крутящий момент, вызывающий Рис.85 закручивание вала на один радиан) через с: с = =

где G — модуль упругости при сдвиге; d — диаметр вала; ℓ — длина вала.

Воспользовавшись принципом Даламбера (инерцией массы стерж­ня пренебрегаем), получим дифференциальное уравнение крутильных колебаний диска, приравняв крутящий момент c·φ, действующий в ва­ле при его закручивании на угол φ , моменту сил инерции массы диска:

+ c·φ =0

где — момент инерции диска относительно оси стержня, перпенди­кулярной к плоскости диска. Для диска постоянной толщины h, изготовленного из материала с удельным весом γ, получим =

Здесь D — диаметр диска; Q — вес диска. Обозначив ω² = дифференциальное уравнение перепишем в виде: + ·φ =0 Общее решение этого уравнения будет φ = А + В

Период колебаний рассматриваемой системы T = = 2π

Для стержня постоянного диаметра d имеем T = 2π а частота колебаний f = =

Вынужденные колебания систем c одной степенью свободы при гармоническом возбуждении

Уравнение вынужденных колебаний системы с одной степенью свободы (рис. 84) получим, если в дифференциальное уравнение ẍ + cx = О кроме сил инерции и сил упругости, действующих на груз Q, учтем влияние периодической вынуждающей силы - Р·соs рt (здесь р - угловая частота вынуждающей силы) ẍ + cx = Р·соs рt

Обозначив: ω² = и q = приведем уравнение к виду ẍ + ω²х = q· соs рt При р малом по сравнению с ω членом ẍ можно пренебречь и считать, что имеет место только статическая деформация, максимальное значение которой = Для определения динамической деформации необходимо решить уравнение ẍ + ω²х = q· соs рt . Решение уравнения будет состоять из суммы: • общего решения однородного уравнения (при q· соs рt = 0) х = А + В •и частного решения уравнения х = C·соs рt

Подставив частное решение в дифференциальное уравнение , найдем С =

Тогда общее решение уравнения будет x = А + В + соs рt

Первые два слагаемых правой части решения , характеризуют свободные колебания, которые обычно быстро затухают; послед­нее характеризует вынужденные установившиеся колебания с угловой частотой р (с периодом Т₁= 2п/р или частотой f = р/2π Гц) и амплитудой С = Амплитуда вынужденных колебаний существенно зависит от соотношения собственной ω и вынужденной р частот ко­лебаний и может быть охарактеризована так называемым коэффици­ентом динамического усиления - β. β = = : = = или β =

где Т₁= ; Т =

Как видно, при малом отношении и С → Когда же частота вынужденных колебаний р→ω, т. е. , р/ω → 1, то С→∞. Когда р = ω, имеет место состояние резонанса. Соответствующая частота вынуждающей силы р = р_кр при этом называется критической. График зависимости ІβІ = f(р/ω), приведенный на рис.86 и представ­ляющий собой так называемую амплитудно-частотную характеристику, позволяет проанализировать поведение колебательной системы в зависи­мости от соотношения частот свободных ω и вынужденных р колебаний.

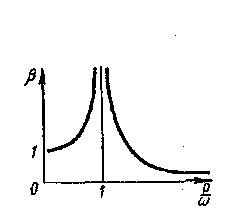
Рис. 86

Пример: Электродвигатель весом Q=400 кг делающий n=1000 оборотов в минуту установлен на консольной балке, состоящей из двух швеллеров длиной 100 см(от опоры до центра масс двигателя). Вертикальная составляющая центробежной возмущающей силы, возникающая от неуравновешенности ротора и подвижной части технологического оборудования равна 25% веса двигателя, т.е. в нашем случае Р = 100 кг. Закон изменения возмущающей силы Р· Подобрать сечение швеллеров, с учетом динамического воздействия колебаний. Решение: При запуске электродвигателя частота вращения ротора будет возрастать от нуля, до 1000 оборотов в минуту. Чтобы резонанс не наступил при запуске или остановке двигателя необходимо, чтобы частота собственных колебаний балок должна быть больше максимального значения частоты вынуждающей силы( не менее чем на 30%), т.е. n_собств=1,3·n = 1300 об. в мин. Или _собств= = = 136 сек^-1 Мы знаем, что = = 136 сек^-1 Откуда = = =0,053 (см) С другой стороны величину статического прогиба балки от веса электродвигателя легко выразить по формуле Мора, с применением правила Верещагина в таком виде = откуда = = = 629 см⁴ Ближайший больший швеллер № 16 имеет осевой момент инерции = 747 см⁴ Тогда для балки из двух швеллеров № 16 = = = = 147 сек^-1 т.е. n_собств= = =1400 об. в мин. Это больше частоты возмущающей силы на 40% Проверим прочность консолей = = = = 216( ) коэффици­ент динамического усиления β = = = 2,04 тогда, с учетом динамического воздействия возмущающей силы = = 2,04· = ±110 ( )

= + =216 +110 = 326 должно быть меньше допускаемого напряжения.