10. Устойчивость плоской формы изгиба

Если одна из главных жесткостей изгиба мала по сравнению с другой, то, изгибая стержень в плоскости наибольшей жесткости, можно, постепенно уве­личивая нагрузку, достигнуть предела, когда плоская форма изгиба перестает быть устойчивой. Ось стержня искривляется в плоскости наименьшей жест­кости, причем отдельные поперечные сечения стержня поворачиваются. Вместо плоского изгиба создается изгиб оси по линии двоякой кривизны, сопровож­дающийся кручением. Критическая нагрузка балки зависит от жесткости на кручение и на изгиб в плоскости действия нагрузки. Устойчивость балки будет зависеть от размеров поперечного сечения и ее свободной длины.

Рассмотрение устойчивости плоской формы изгиба пока остается за пределами программы курса сопротивления материалов для строителей и архитекторов.

Тема 18 Продольно-поперечный изгиб.

Литература. Г.С.Писаренко Справочник по сопротивлению материалов §18.7 Вопросы. 1. Особенности работы конструкций при продольно-поперечном изгибе. 2. Определение напряжений при продольно-поперечном изгибе.

1. Особенности работы конструкций при продольно-поперечном изгибе. Продольно-поперечным изгибом называется сочетание поперечного изгиба со сжатием или растяжением бруса. При расчете на продольно-поперечный изгиб вычисление изгибающих моментов производится с учетом прогибов оси. Т.е. гипотеза малости деформаций не применима. Так же не применим принцип независимости действия сил.

Рассмотрим балку, загруженную двумя видами воздействий. Продольной сжимающей силой (N), приложенной центрально, величина которой заведомо меньше критической величины. И произвольной поперечной нагрузкой, которую на чертеже обозначим одной результирующей силой (Р). Изобразим три состояния. Рис.70

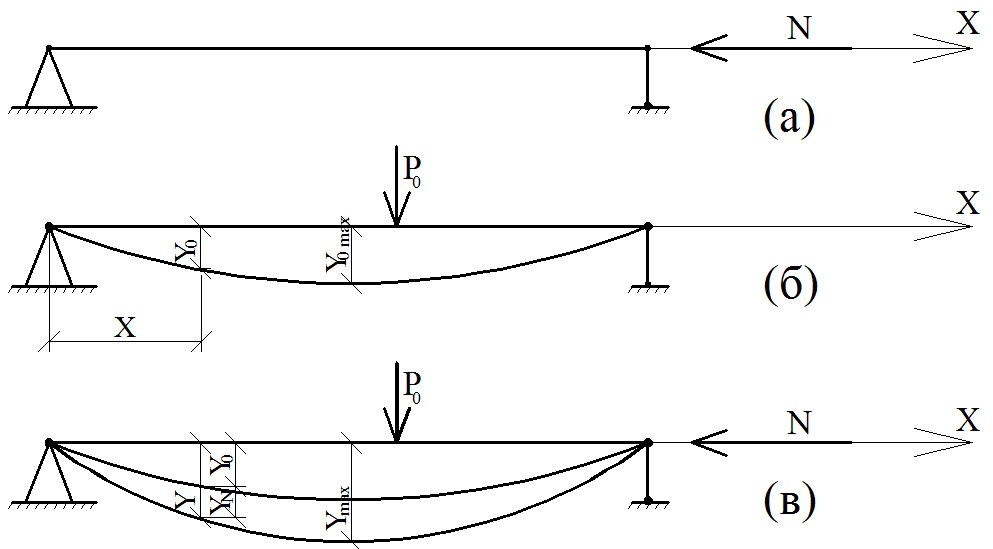
Рис.70

На первом (рис.70 а)приложена только продольная нагрузка. Поскольку величина силы меньше критической величины то поперечных деформаций не произойдет и стержень останется прямолинейным.

Во втором состоянии (рис.70 б) приложена поперечная нагрузка, которая вызывает искривление продольной оси. При этом произвольная точка на расстоянии Х от начала координат переместится. Обозначим прогиб как У₀

Момент изгибающий в этом сечении обозначим как М₀

В третьем состоянии (рис.70 в) одновременно действуют поперечная и продольная нагрузка. Тогда в произвольной точке деформированной оси величина изгибающего момента будет состоять из двух частей М = М₀ + N·У Понятно, что если величина момента при одновременном действии поперечной и продольной нагрузки больше, чем только от поперечной, то и величина прогиба будет отличаться. У = У₀ + У_N Но, при приложении только продольной нагрузки прогиб отсутствует. Т.е. прогиб при одновременном действии сил не равен прогибу от порознь действующих сил. Дифференциальное уравнение изогнутой оси имеет вид: = - = - Знак минус у момента используем в соответствии с правилом знаков, потому, что растянуты нижние волокна. Преобразуем для наглядности его следующим образом: + = - здесь составляющая прогиба от поперечной (балочной) нагрузки = - Тогда - = - или = - здесь дополнительный прогиб, возникающий от продольной нагрузки у стержня, предварительно изогнутого поперечной нагрузкой. Предположим, что форма изогнутой оси дополнительной деформации синусоида. = Δ тогда = - отсюда - = - или - = - раскрыв скобки - + = - и перенеся У влево, а У_о вправо - + = - приводим подобные - ·( - = -

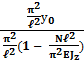
= = = выражение стоящее в знаменателе по форме напоминает формулу Эйлера. Отличие заключается в том, что в формуле Эйлера используется минимальный момент инерции, а в данном случае момент инерции берется относительно той оси, относительно которой искривляется поперечной нагрузкой продольная ось балки. Обозначим, для удобства эту величину как Р_эйл Р_эйл = тогда =

Полученная формула дает приемлемые результаты при N < 0,8 P_кр

Отношение является критерием жесткости.

Если → 0 жесткость велика и продольный изгиб можно не учитывать. Если =0 то у = у₀

Если →1 жесткость мала, балка гибкая. При Р_эйл у = →∞

2. Определение напряжений при продольно-поперечном изгибе.

Напряжения при продольно-поперечном изгибе определяются как алгебраическая сумма напряжений от трех действующих факторов. Продольной силы, изгибающего момента от поперечной нагрузки и изгибающего момента от продольной нагрузки, возникающего из-за искривления продольной оси. Последний достигает экстремального значения в точке, где возникает максимальный прогиб. Максимальный момент от поперечной нагрузки может не совпадать по положению с точкой максимального прогиба. Поэтому положение опасного сечения при продольно-поперечном изгибе определяются неоднозначно. Как правило, условие прочности составляется для нескольких сечений.

В общем виде (без учета знаков) напряжение равно: б = + + = + + Если сечение симметрично относительно оси Z , продольная сила сжимающая, материал балки одинаково сопротивляется растяжению и сжатию и положение точки максимального прогиба совпадает с сечением, где действует максимальный момент, то опасной точкой сечения будет точка 1, где все три компоненты напряжения совпадают по знаку (по виду деформации – сжатие). (Рис.70 в) б = - - - ≤ [б]

При прочих аналогичных условиях, если продольная сила растягивающая опасной будет точка 2. Условие прочности имеет вид б = + + ≤ [б]

По условиям прочности можно решить три задачи: а) проверочный расчет б) определение грузоподъемности в) проектировочный расчет ( подбор сечения для заданной нагрузки).

а) проверочный расчет выполняется сравнением величины, полученной в левой части выражения напряжения после подстановки заданных величин нагрузок и сечения с величиной допускаемого напряжения в правой части.

б) определение грузоподъемности возможно при заданном значении одной из нагрузок. Либо продольной, либо поперечной.

в) проектировочный расчет выполняется методом последовательных приближений.

В первом приближении вычисляется требуемый момент сопротивления из условия прочности на поперечный изгиб для сечения, где действует максимальный изгибающий момент от поперечной нагрузки по уменьшенному значению допускаемого напряжения. б = ≤ 0,6·[б] отсюда находим

Во втором приближении выполняется проверка этого же сечения на одновременное действие продольной и поперечной нагрузки. При необходимости уточняются размеры сечения.

б = - - ≤ [б]

В третьем приближении выполняется проверка прочности сечения, где находится максимальный прогиб. Следует обратить внимание, что величина балочного момента может иметь в этом сечении другую величину, отличную от .

б = - - - ≤ [б]