4. Пределы применимости формулы Эйлера.

Напряжения могут изменяться от нуля до предела пропорциональности. Выразим критическое напряжение б_кр= = здесь = преобразуем выражение напряжения к следующему виду б_кр= в знаменателе которого находится некоторая величина, одновременно характеризующая совокупность геометрических характеристик стержня: длину участка, деформированная ось которого является половиной синусоиды и радиус инерции поперечного сечения. Назовем ее гибкостью и обозначим как λ λ = тогда б_кр= В полученном выражении величины напряжения и гибкости переменны, а стоящие в числителе постоянны. Т.е. мы получили зависимость между гибкостью и напряжением, которая является гиперболической. Построим график этой зависимости рис. 64

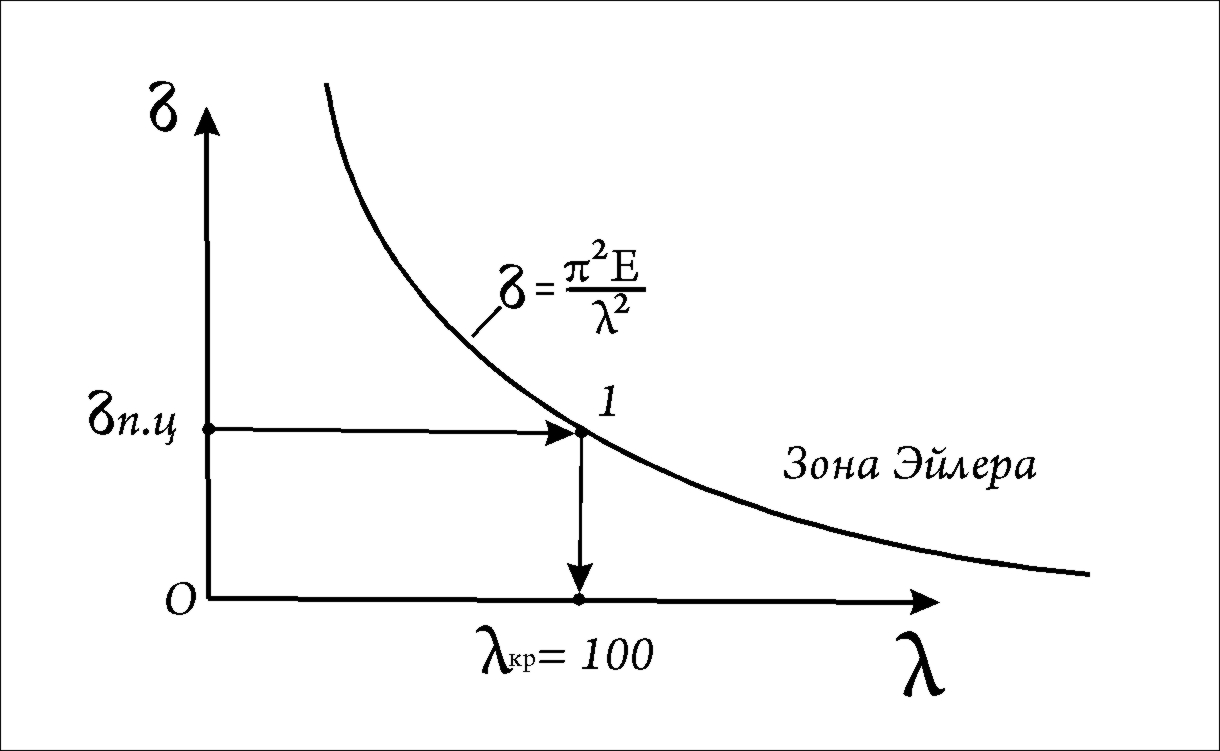
Рис.64

Отложив на оси напряжений значение предела пропорциональности, проведем через эту точку прямую, параллельную оси гибкости до пересечения с гиперболой Эйлера. Получим точку 1. Формула Эйлера справедлива в промежутке от нуля до б_пц по напряжениям . По гибкости эта зона лежит правее λ_кр , значение которой легко вычислить, подставив в выражение б_кр= значение б_пц . Например, для конструкционной стали СТ3 предел пропорциональности б_пц= 2000 кг/см² ; ≈ 10 ; Е = 2·10⁶ кг/см² тогда λ = = = 100

5.Потеря устойчивости при напряжениях превышающих предел пропорциональности. При малом значении гибкости от нуля до, примерно 40 ÷ 60, критическое значение напряжения значительно меньше того, которое определяется по формуле Эйлера и сохраняет постоянную величину равную б_т . В промежутке между λ= 40÷60 и λ=100 для конструкционных сталей зависимость между критическими напряжениями и гибкостью достаточно хорошо (Рис.65) аппроксимируется прямой 1-2 . Продолжим прямую 1-2 до пересечения с осью б. Обозначим значение напряжения в этой точке как «а». Тогда в любой точке на участке 1-2 значение критического напряжения легко определить как б_кр= а - или как λ = а - 𝒃·λ если обозначить = 𝒃 Полученное выражение λ = а - 𝒃·λ принято называть формулой Ясинского.

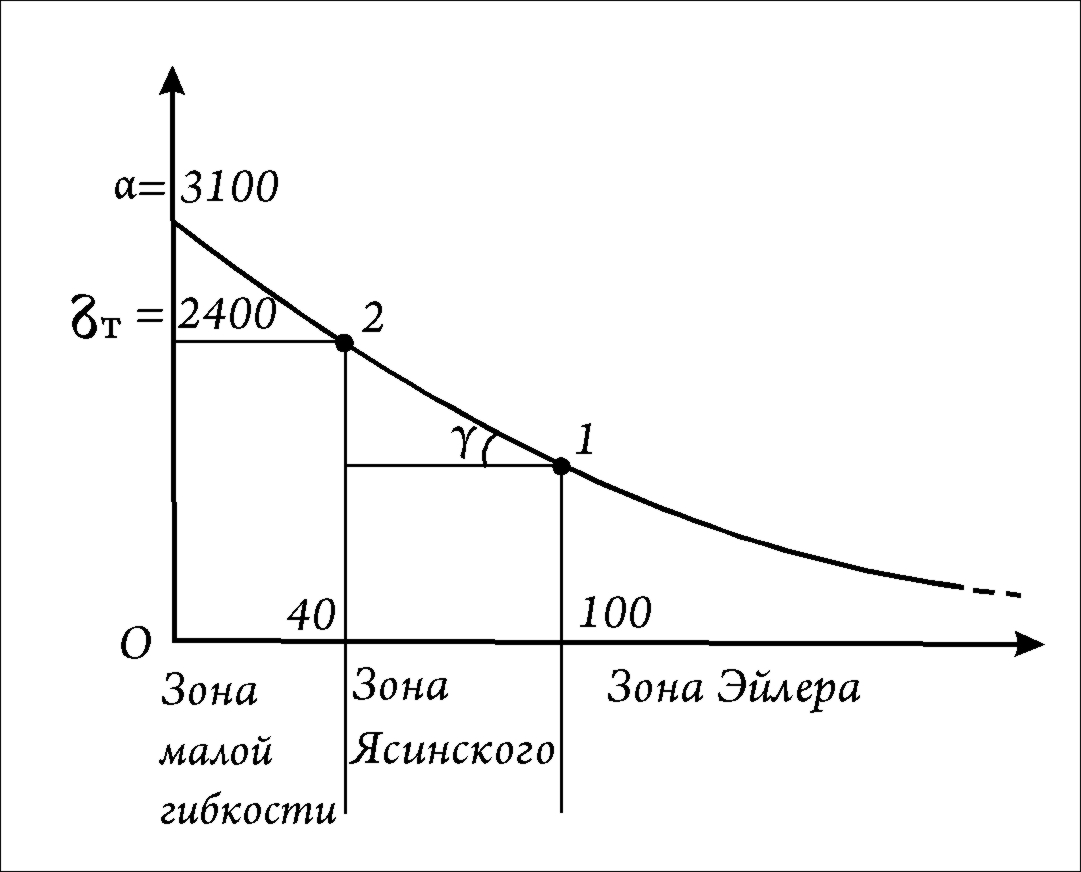
Рис.65

Для чугуна аппроксимация экспериментальных данных для критического напряжения в зоне Ясинского точнее по квадратичной формуле. λ = а - 𝒃·λ + с· где с=0,53

	λкр	а (кг/см2 )	b
ст 3	100	3100	11,4
ст 5	100	4640	32,6
ст 40	90	3210	11,6
кремнистая сталь	100	5890	38,2
дерево(сосна)	110	293	1,94
чугун	80	7760	120

Следует иметь в виду, что поскольку уровень допускаемых напряжений меньше, чем предел текучести, то при малых значениях гибкости расчет на устойчивость не актуален. В этой зоне практикуется расчет на прочность.

6.Практический расчет на устойчивость.

При малых гибкостях продольно сжатые стержни теряют несущую способность от потери прочности. Условие прочности формулируется следующим образом: б_действ ≤ [б] = Для пластичных материалов = Для хрупких материалов = коэффициент запаса n = 1,5 . При больших значениях гибкости они теряют несущую способность от потери устойчивости прежде, чем от потери прочности. Условие устойчивости б_действ ≤ [б]_у = причем всегда больше чем n (почему: на практике всегда либо сила приложена с эксцентриситетом, либо есть начальная кривизна, либо какой-то другой , хоть и малый, дефект). Значения коэффициентов запаса на устойчивость предписываемое СНиПами колеблется в следующих пределах.

	nу
для стали	от 1,8 до 3,0
для чугуна	от 5,0 до 5,5
для дерева	от 2,8 до 3,2

Запишем в виде соотношения = или = · Выражение по сути является коэффициентом уменьшения основного допускаемого напряжения при сжатии, обозначим его как φ Тогда = · φ и условие устойчивости приобретает вид б_действ = ≤ · φ

Значения коэффициента уменьшения основного допускаемого напряжения приведено в таблице для наиболее часто используемых материалов и для допустимых значений гибкости.

	Коэффициент	φ для
Гибкость λ	ст2 , ст3, ст4	ст5	чугун	дерево
0	1,00	1,00	1,00	1,00
10	0,99	0,98	0,97	0,99
20	0,96	0,95	0,91	0,97
30	0,94	0,92	0,81	0,93
40	0,92	0,89	0,69	0,87
50	0,89	0,86	0,57	0,80
60	0,86	0,82	0,44	0,71
70	0,81	0,76	0,34	0,60
80	0,75	0,70	0,26	0,48
90	0,69	0,62	0,20	0,38
100	0,60	0,51	0,16	0,31
110	0,52	0,43		0,25
120	0,45	0,36		0,22
130	0,40	0,33		0,18
140	0,36	0,29		0,16
150	0,32	0,26		0,14
160	0,29	0,24		0,12
170	0,26	0,21		0,11
180	0,23	0,19		0,10
190	0,21	0,17		0,09
200	0,19	0,16		0,08

Расчет на устойчивость может выполняться как проверочный, либо как проектировочный.

7.Проверочный расчет сжатых стержней.

Порядок проверочного расчета на устойчивость при использовании таблицы коэффициентов снижения основного допускаемого напряжения следующий: 1) исходя из известных размеров и формы поперечного сечения, определяем наименьший осевой момент инерции J_мин , площадь А_брутто , вычисляем минимальный радиус инерции и гибкость. i_мин = λ = 2) по таблице находим коэффициент φ и вычисляем допускаемое напряжение на устойчивость = · φ 3) теперь достаточно сравнить величину действующего напряжения с найденной величиной допускаемого б_действ= ≤ · φ Превышение действующим напряжением допускаемого значения недопустимо. Но и разница между ними не должна быть значительной, потому что ведет к перерасходу материала (лучше, если она не превышает 5%).

8.Проектировочный расчет сжатых стержней.

Расчет требуемых размеров поперечного сечения производится методом подбора. В формуле ≤ · φ одновременно неизвестны А_брутто и φ 1) Поскольку значение коэффициента уменьшения основного допускаемого напряжения изменяется в пределах от 0 до 1 зададимся средним значением φ= 0,5 и вычислим требуемое значение А_брутто ≥

2) По принятой величине площади поперечного сечения определяем линейные размеры, и геометрические характеристики и i_мин

3) Затем вычисляем λ = и по таблице находим соответствующую величину φ₁ Вероятнее всего, что полученная величина не совпадёт с принятой φ= 0,5

4)Повторим расчет, задавшись новым значением коэффициента уменьшения основного допускаемого напряжения равным среднему между принятым и полученным φ₂= А_брутто ≥ → и i_мин → λ = и по таблице → φ₃ Подбор производим до тех пор, пока принятое и полученное значение φ не совпадут, или будут отличаться на минимально допустимую, наперед заданную величину.

9. Частные случаи загружений и схем, чаще других встречающиеся на практике.

1)Колонна, загруженная распределенной нагрузкой. Рис.66 Р_кр =(qℓ_кр) = где μ=1,12

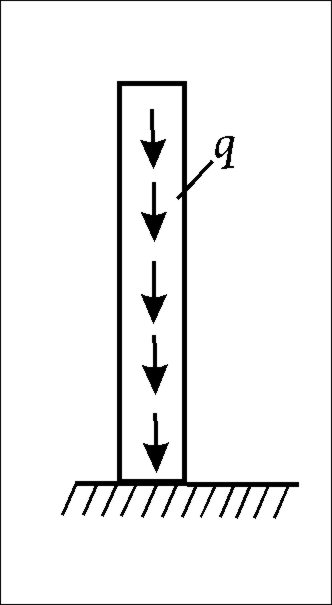Рис.66 2)Две силы. Рис. 67 Р_кр = Р₁+Р₂ = μ = · где α = m=

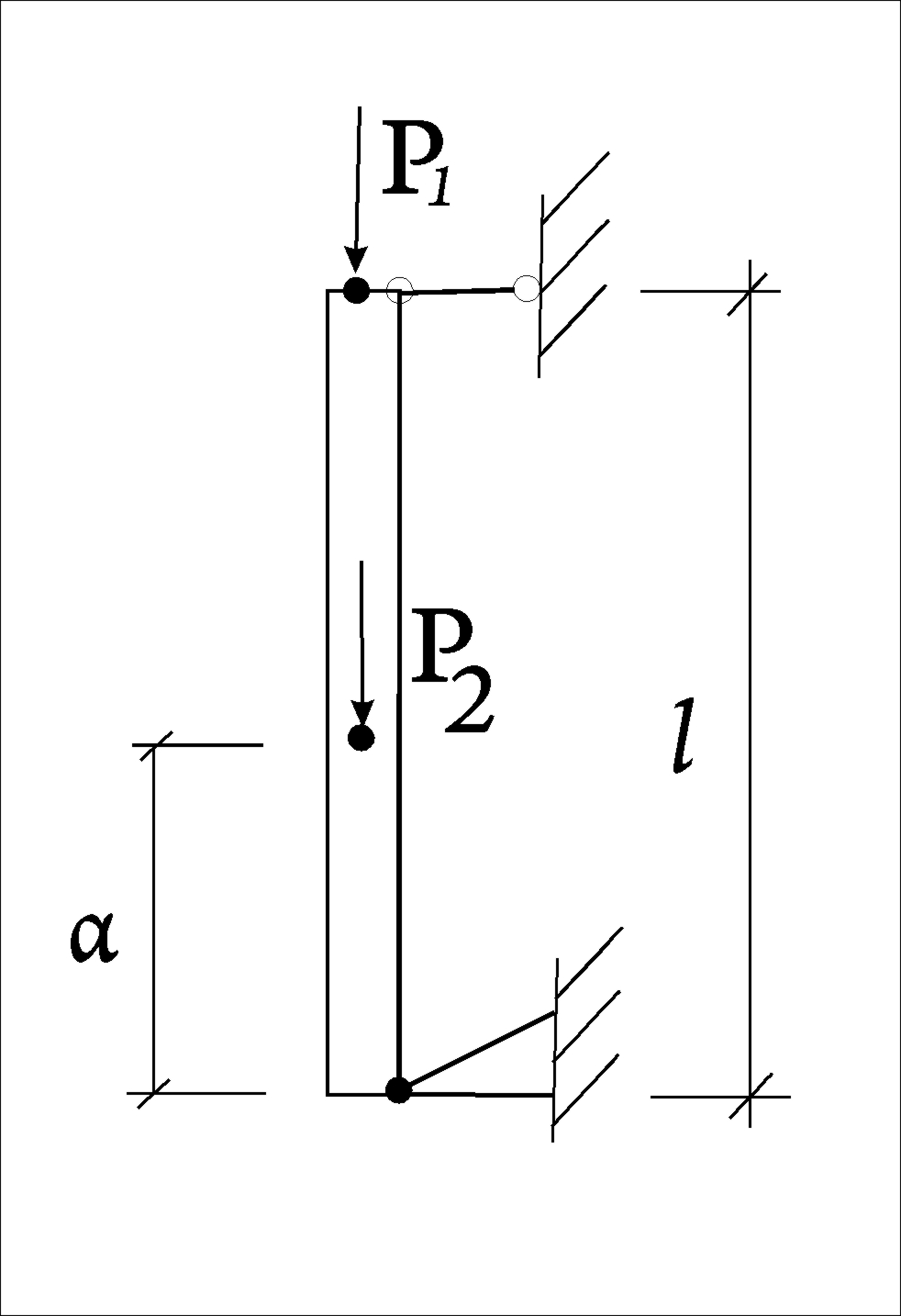
Рис.67

3)Колонна, состоящая из двух частей, разного сечения. Рис.68 Р_кр = μ= n=

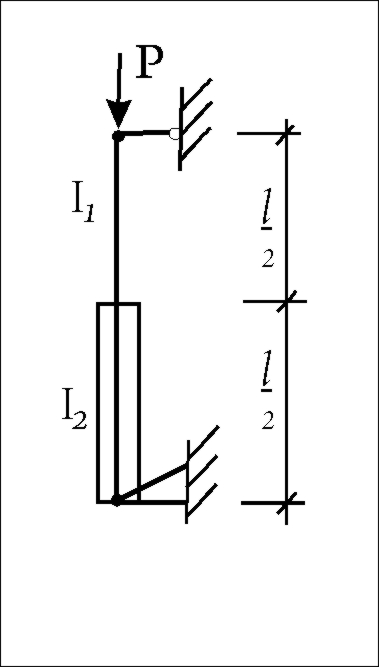
Рис.68

4) Особую проблему представляют расчеты на устойчивость сжатых тонко­стенных стержней незамкнутого сечения. В отличие от монолитных стержней такие стержни теряют устойчивость, не только изгибаясь, но и закручиваясь. Форма потери устойчивости, при которой возникает угол закручивания, называется изгибно-крутильной формой потери устойчивости. При этой форме каждое сечение поворачивается вокруг некоторой мгновенной оси, параллельной оси стержня. Если же сечения получают только поступательное перемещение без закручивания, то эта форма называется изгибной формой потери устойчивости. Таким формам, имеющим место в плоскости главных осей инерции сечения, соответствуют эйлеровские критические силы.

При загружении продольной сжимающей силой стержня имеющего тонкостенное сечение (рис.69) принято определять: критическую силу в плоскости наибольшей жесткости (Р_у), критическую силу в плоскости наименьшей жесткости (Р_z), критическую силу, соответствующую крутильному эффекту (Р_ω), критическую силу в изгибно-крутильной форме по Власову ( Р_В)

Р_у= Р_z= Р_ω= ) Р_В= здесь = Y_c+Y_a = +

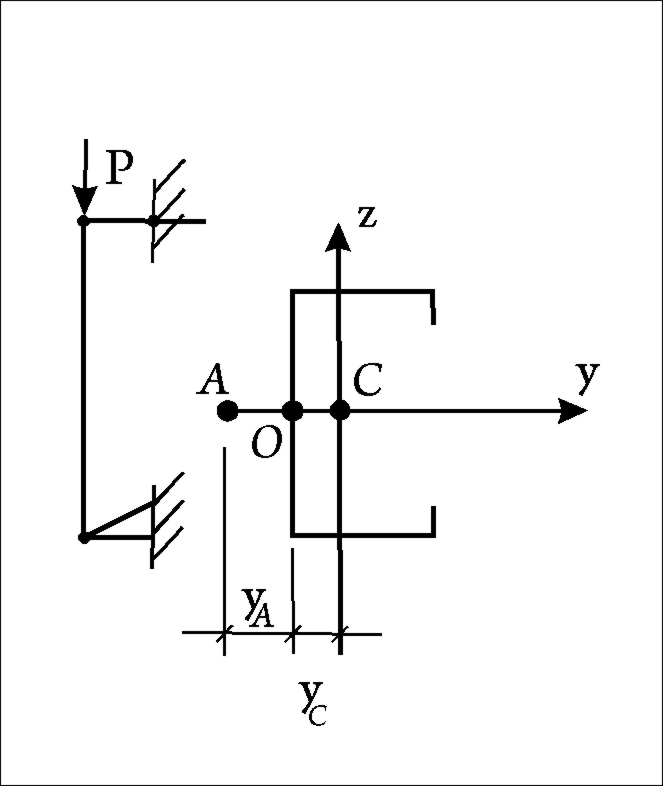
Рис.69