2.Определение критической силы при центральном сжатии прямолинейных стержней.
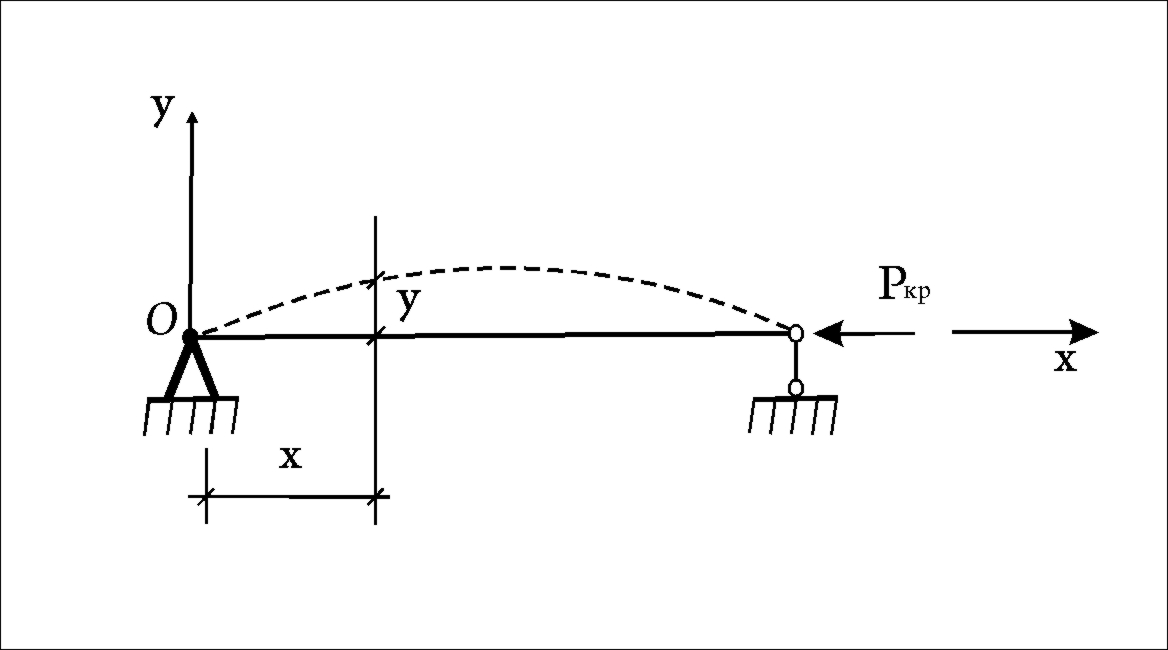
Рис.62
Пусть
прямолинейный стержень (рис.62) центрально
загружен одной сжимающей силой Р
величина которой, плавно возрастая от
нулевого значения достигла критического
значения. При этом величины напряжений,
так же возрастая от нулевых значений,
не достигли при этом предела
пропорциональности, т.е. находятся в
пределах применимости закона Гука.
Изобразим оба вероятностных состояния
деформации стержня - прямолинейную
и изогнутую. В
произвольном сечении на расстоянии Х
от начала координат, находящегося в
крайней левой точке балки, перемещение
оси балки из прямолинейной формы в
криволинейную равно прогибу балки У.
Мы уже знаем приближенное
дифференциальное уравнение изогнутой
оси, которое имеет вид: 
= 
Изгибающий момент в изогнутом состоянии
возникает от приложенной силы М= -
Ркр·у (знак минус появился
потому, что растянуты здесь верхние
волокна). Преобразуем выражение к
виду: 
+ 
= 0 или введя обозначение
= 
+
·y
= 0
Общий интеграл однородного дифференциального уравнения имеет вид:
У =
А·
+ B·
Произвольные
постоянные А и В определим из начальных
условий
1) при х=0 на опоре У = 0 0 = А·
+ B·
т.к. 
=0
то А может быть любым тогда при
= 1 В должно быть равно нулю. Тогда
исключим второе слагаемое из дальнейшего
рассмотрения. У = А·
2) при х=ℓ на
правой опоре У = 0 т.е. 0 = А·
А не может равняться нулю, иначе
уравнение вырождается в бессмысленное,
т.е.
= 0 это возможно при 
= nπ где n=1,2,3 … при n=1 уравнение
оси дает половину синусоиды. При n=2
уравнение оси дает полную синусоиду.
Многочисленные эксперименты
показывают, что значительно чаще
образуется одна полуволна, и что форма
образующейся изогнутой оси носит
вероятностный характер. Поэтому расчет
будем вести при n = 1 т.е.
= π подставим
значение 
возведя выражение в квадрат, для
удобства работы.
или 
отсюда
Ркр
=
выведенную формулу первым получил
Леонардо Эйлер( профессор Санкт
Петербургской Академии наук) и она носит
его имя.
Формула имеет ограничения в применении. Во первых. Она справедлива только для случая, когда деформированная ось имеет форму половины синусоиды. Во вторых. Величины напряжений должны лежать в пределах пропорциональности.