Тема 17 Устойчивость.
Литература: Г.С.Писаренко Сопротивление материалов глава 19
Вопросы: 1. Основные понятия. 2. Определение критической силы при центральном сжатии прямолинейных стержней. 3. Учет условий закрепления концов стержней. 4. Пределы применимости формулы Эйлера. 5. Потеря устойчивости при напряжениях превышающих предел пропорциональности. 6. Практический расчет на устойчивость. 7. Проверочный расчет сжатых стержней. 8. Проектировочный расчет сжатых стержней. 9. Частные случаи загружений и схем, чаще других встречающиеся на практике. 10. Устойчивость плоской формы изгиба.
1. Основные понятия. Устойчивостью называется способность тел сохранять под нагрузкой первоначальное равновесие формы деформации. Рассмотрим несколько примеров.
Рис.59
Пусть к балке изображенной на рис.59 приложена переменная по величине сила Р. При малых значениях силы балка, испытывающая поперечный изгиб деформируется в плоскости хоу . По мере увеличения силы прогиб в направлении оси У растет, но положение оси Z остается неизменным. Но наступит такой момент, при достижении силой значения называемого критическим, когда сечение, в котором приложена сила, повернется вокруг оси Х и сместится вдоль оси Z. Плоский прямой поперечный изгиб превратился в кручение с косым изгибом.
Рис.60
Пусть к валу изображенному на рис.60 приложен в точке В переменный крутящий момент Мкр. При малых значениях момента ось Х остается прямолинейной и стержень работает на кручение. При достижении моментом критической величины ось Х искривится и ( если стержень изготовлен из капрона, резины и т.п.) образуется петля. Кручение превратилось в сложный изгиб с кручением.
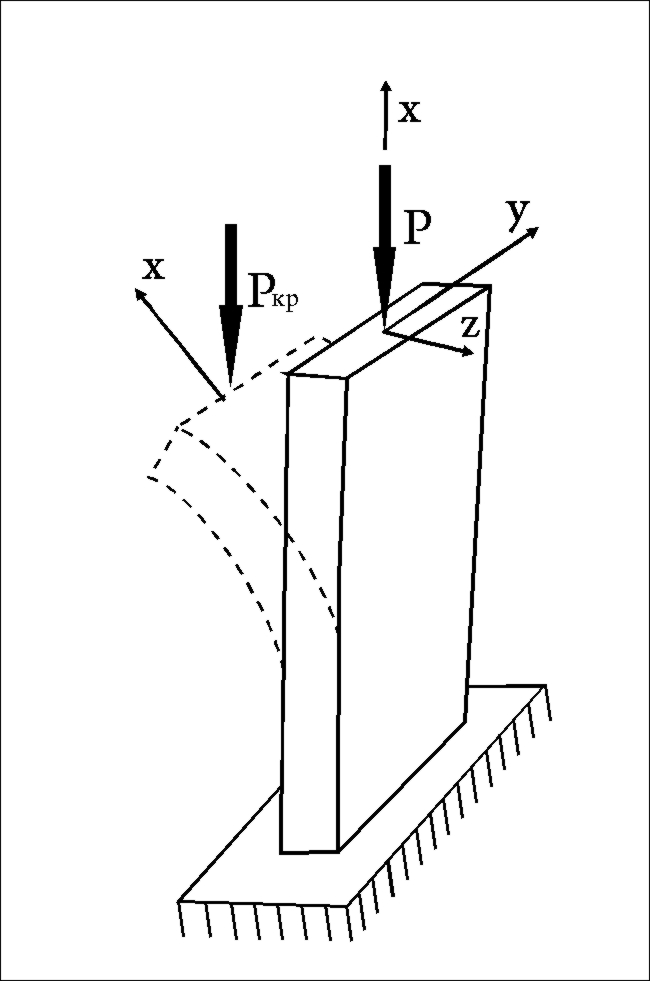
Рис.61
Пусть к прямолинейному стержню изображенному на рис.61 приложена центрально сжимающая сила изменяющаяся от нуля до Р. При малых значениях силы стержень испытывая центральное сжатие будет укорачиваться, сохраняя прямолинейную ось Х. При достижении силой критического значения ось Х искривится. Центральное сжатие превратилось в сжатие с изгибом.
Во всех приведенных примерах при достижении силовым фактором критического значения происходит потеря устойчивости первоначальной формы деформации и переход ее в новую форму деформирования. При величинах нагрузок, меньших критического значения форма деформации сохраняется устойчиво. Принято это состояние называть устойчивым. Если при этом состоянии уменьшить или снять нагрузку, конструкция восстановит свою первоначальную форму и размеры. Момент, когда происходит потеря устойчивости, принято называть критическим или неустойчивым равновесием. В этот момент обе формы равновесия равновероятны. Сразу после наступления неустойчивого равновесия величины напряжений и деформаций значительно возрастают, что приводит к разрушению конструкции. Т.е. критическое значение нагрузки – максимальное из всех, которое может выдержать конструкция, не разрушившись и в пределах допустимых деформаций. Момент неустойчивого равновесия длится очень малое время и всегда приводит к разрушению конструкции, если нет специальных мер, ограничивающих величину деформаций.
Наиболее часто встречающейся в строительстве формой потерей устойчивости является потеря устойчивости при центральном сжатии. Ее мы и рассмотрим.