3 .3 Стесненное кручение тонкостенных стержней открытого профиля

Если на тонкостенный стержень открытого профиля наложены связи, пре­пятствующие свободному перемещению точек контура при действии крутящих моментов, то такой вид кручения носит название стесненного (изгибного) кру­чения. Примером стесненного кручения может служить стержень двутаврового профиля с жестко защемленным концом, если к свободному концу приложена скручивающая пара М_х (рис.57, а).

Защемленное сечение остается плоским, следовательно, препятствует свободной депланации (т. е. упругим перемещениям вдоль оси стержня) смежного с ним сечения. Чем дальше от защемления находится поперечное сечение, тем свободнее его деплана­ция. Значит, депланация соседних сечений различна. Поэтому и расстояния между отдельными точками этих сечений изменяются, т. е. изменяются длины продольных волокон. При этом полки двутавра искривляются (изгибаются). Происходит изгиб частей стержня в отсутствии внешнего изгибающего фактора. Но при изгибе происходит удлинение продольных волокон а следовательно и возникновение в сечении нормальных напряжений, направленных вдоль оси Х . В рассматриваемом случае изгибного кручения двутавра система внутренних продольных усилий, действующих в поперечных сечениях полок, приводится к двум парам, направленным в противоположные стороны (рис. 57 ,б). Совокупность двух таких пар, противоположно направленных, лежащих в параллельных плоскостях, называется бипарой (двойной парой). Величина бипары оценивается бимоментом В_ω, равным произведению мо­мента М каждой пары на расстояние между ними h (плечо бипары). В_ω = М·h (кг·см²). Но, до тех пор, пока неизвестна величина нормальных напряжений, вычислить бимомент таким способом невозможно. C другой стороны В_ω = ·ω·dA

Кроме нормальных напряжений, в сечении возникают касательные напря­жения двух родов: а) касательные напряжения τ_к, соответствующие свободному кручению (рис.57 ,в). Эти напряжения получаются от части общего крутящего мо­мента Мх, которая идет на чистое кручение и обозначается через Мк; Замкнутый поток τ_к показан на рис.57в. б) секториальные касательные напряжения τ_ω, возникающие в связи с появлением нормаль­ных напряжений . Эти напряжения вызываются изгибно-крутящим моментом М_ω, который составляет вторую часть общего крутящего момента М_х. Секториальные касательные напряжения τ_ω принимаются равномерно распределенными по толщине стенки сечения (рис.57, г). Момент двух незамкнутых потоков касательных напряжений τ_ω относительно центра изгиба равен изгибно-крутящему моменту М_ω.

Причем М_х = М_к + М_ω Величины составляющих М_х не могут быть определены из условий равновесия отсеченной части стержня.

При изучении закона распределения напря­жений при кручении тонкостенных стержней ис­ходят из следующих двух дополнительных предположений: 1) деформации сдвига срединной поверхности стержня равны нулю; 2)проекция контура поперечного сечения не деформируется, т. е. при деформации стержня проекция расстояния между двумя точками контура на плоскость поперечного сечения остается постоянной.

Закон изменения секториальных нормальных напряжений по сечению выражается уравнением = —Е·θ΄΄·ω

Из этого выражения видно, что при стес­ненном кручении тонкостенного стержня нормаль­ные напряжения в поперечном сечении распреде­ляются по закону секториальных площадей ω (т.к. и модуль упругости и вторая производная от угла закручивания в сечении не изменяются). Кроме того, если θ΄- постоянная величина (например при свободном кручении), то θ΄΄= 0, а следовательно нормальные напряжения при свободном кручении возникнуть не могут) . Закон изменения секториальных касатель­ных напряжений в сечении выражается уравне­нием

τ_ω=

откуда видно, что секториальные касательные напряжения τ_ω в поперечном сечении стержня изменяются по закону изменения секториального статического момента . Подставим в формулу бимомента закон распределения б_ω В_ω = ·ω·dA = Здесь = J_ω Откуда = - Величина бимомента прямо пропорциональна второй производной от угла закручивания. Подставив выражение в формулу закона распределения б_ω получаем

б_ω= ω

Если взять производную от бимомента = -E = = получим взаимосвязь между бимоментом и изгибно-крутящим моментом.

Итак: при расчете тонкостенных стержней, находящихся в условиях стесненного кручения Нормальные напряжения следует определять по формуле б_ω= ω где В — расчетный бимомент,(кг ·см²) J_ω - секториальный момент инерции ( см⁶); ω — секториальная площадь (координата),( см²). Секториальные касательные напряжения τ_ω = где М_ω — изгибно-крутящий момент(кг· см) — секториальный статический момент отсеченной части сечения, заклю­ченной между начальной точкой контура, для которой S_ω = 0, и той точкой, где τ_ω вычисляется; δ— толщина стенки сечения в точке, где определяется касательное напряжение.(см)

Наибольшие касательные напряжения от чистого кручения τ_к в сечении, состоящем из нескольких прямоугольников, возникают посередине наружного края наиболее широкого прямоугольника профиля _{мах к}=

Для вычисления напряжений по представленным формулам, необходимо предварительно найти значения внутренних усилий , которые из уравнений равновесия найдены быть не могут. Для их вычисления необходимо составить выражение угла закручивания θ = f(х)

Дифференциальное уравнение угла закручивания Напомним, что М_х = М_к + М_ω или М_х = или так - - М_х продифференцировав по х получим ^1v- - дифференциальное уравнение угла закручивания где интенсивность распределенного вдоль оси Х внешнего крутящего момента. Обозначим - = m Тогда М_х = Разделим почленно дифференциальное уравнение на и введя обозначение k²= получим ^1v- k²· решение этого уравнения есть сумма двух, однородного (при m=0 ) , и частного решения (зависящего от правой части).

Рассмотрим решение однородного уравнения ^1v- k²· Общий интеграл имеет вид θ = С₁· + C₂· + C₃·z + C₄ Последовательное дифференцирование дает θ΄= С₁·k + С₂·k· + C₃ вторая производная θ΄΄= k²·(С₁· + С₂· ) третья производная θ΄΄΄= k³·(С₁· + С₂· )

или в таком виде М_к = + C₃ B_ω = - = - М_ω= - = - Складывая М_к+ М_ω = C₃

Для определения произвольных постоянных С₁ , С₂ , С₃ и С₄ применяем метод начальных параметров и после всех преобразований получаем

θ΄ = - B₀ B_ω = - _{0 k0} M_ω= - _{0 k0} здесь , B₀ и _k0 соответственно начальные параметры угла закручивания, бимомента и изгибно-крутящего момента из условий закрепления.

Уравнение угла закручивания для любого участка составляются аналогично тому, как это делалось при составлении уравнения прогибов балки при поперечном изгибе. Так же вместо Z подставляем (Z-а_i), при этом через а_i обозначаем расстояния от левого конца стержня до начала участка. Таким образом имеем окончательно θ=θ₀+ + + [(z-а_i)- ]

Далее путем последовательного дифференцирования могут быть получены общие уравнения для бимомента и изгибно-крутящего момента для любого участка и загружения.

Для облегчения построений всех эпюр следует иметь в виду аналогии зависимостей при поперечном изгибе и стесненном кручении.

Поперечный изгиб	Стесненное кручение
ЕJy''''→q	EJωθ''''→m
ЕJy'''→Q	EJωθ'''→Mω
ЕJy''→M	EJωθ''→Bω
ЕJy'→φ	EJωθ'
у	θ

3.4 Внецентренное растяжение тонкостенного стержня

Рассмотрим стержень двутаврового профиля с жестко защемленным концом, если к свободному концу внецентренно приложена растягивающая сила 4Р.(рис.58 а )

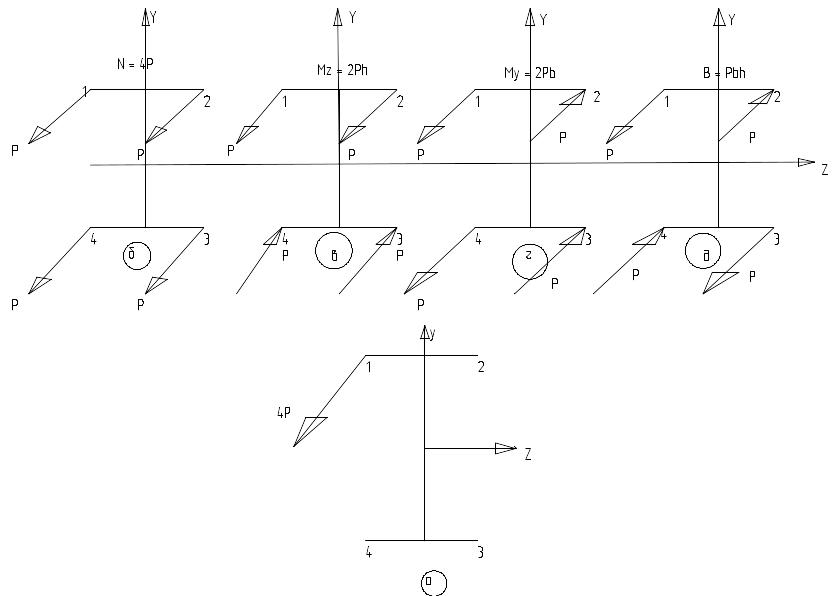
Рис.58

Представим это загружение как сумму четырех, как показано на рисунке. Сумма усилий в точке 1 на схемах б, в, г, д равна 4Р, что соответствует схеме а. Сумма усилий в точках 2 , 3 , и 4 на схемах б, в, г, д равна 0, что так же соответствует схеме а. Усилия, приложенные к схеме б симметричны и их можно свести к одной центрально приложенной силе 4Р. Усилия приложенные к схеме в создают момент относительно оси У ( М_у=2Рh). Усилия приложенные к схеме г создают момент относительно оси Z ( М_z=2Рb). Усилия приложенные к схеме д создают бимомент ( В_ω= Рhb). Здесь hb равно удвоенной площади треугольника 015, т.е. секториальной координате точки 1, точки приложения силы 4Р. Итак, мы разложили внецентренно приложенную силу 4Р на четыре загружения, распределение напряжений в которых нам уже известно. Тогда на свободном конце балки в произвольной точке с координатами y и z нормальное напряжение б = + y + z + ω

Бимомент от системы внецентренно приложенных растягивающих или сжимающих сил следует определять (с учетом знаков) как = . Величина бимомента изменяется по длине балки и достигает в защемлении значения, определяемого по формуле = Напомним, что гиперболические синус и косинус определяются следующим образом =

3.5 Общий случай загружения.

Если к тонкостенному стержню приложена произвольная нагрузка, воздействие которой вызывает появление в сечениях всех уже известных внутренних силовых факторов а именно: N_x , Q_y , Q_z , M_{y ,} M_z и M_x(кр) то, учитывая, что появление крутящего момента приводит к необходимости разложения его на момент чистого кручения, изгибно-крутящий и бимомент ( в случае стесненного кручения), то прежде чем составлять выражение напряжения, необходимо определиться, является кручение стесненным или нет. Кроме того бимомент возникает, как мы видели, от внецентренно приложенной продольной нагрузки. Кроме того, момент чистого кручения, изгибно-крутящий момент и обе составляющие бимомента изменяются в зависимости от характера и величины деформации закручивания стержня и условий опирания.

Определить положенное опасного сечения ( в сколько-нибудь сложном случае) можно только построив эпюры всех внутренних силовых факторов. Причем явно опаснее других одно какое-нибудь сечение бывает на практике, крайне редко. Так же не очевидно положение одной опасной точки в сечении. С учетом всего сказанного выражения напряжений в точке сечения тонкостенного стержня в общем случае загружения имеют вид:

б = + y + z + ω

τ = δ+