3. Расчет тонкостенных стержней открытого профиля.

Расчет тонкостенных стержней открытого профиля значительно сложнее, чем закрытого, и требует предварительного изучения новой темы – секториальных характеристик сечений.

3.1 Секториальные характеристики Секториальная площадь или секториальная координата

На рис.42 изображено поперечное сечение тонкостенного стержня. Пусть выбрана произвольная точка А— полюс. На срединной линии сечения стержня, выбрана произвольная точка М₀ принятая за начало отсчета.

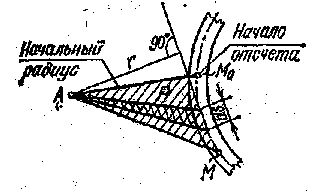
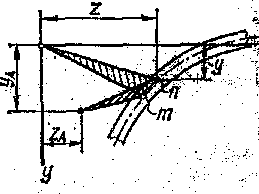
Рис.42 Рис.43 Прямая АМ₀ называется подвижным радиус-вектором(ρ). При вращении радиус-вектора вокруг полюса А его конец перемещается в точку М.

Секториальной координатой точки М называется удвоенная площадь сек­тора АМ₀М, ограниченного участком срединной линии и радиус-векторами, про­веденными из полюса к концам участка. Эта площадь выражается интегралом ω_м=

где ω_м — секториальная площадь, или секториальная координата, имеющая размерность см², r— перпендикуляр, опущенный из полюса А на направление касательной к средней линии на участке dS; S — длина дуги М₀М

Зависимость между секториальными координатами при различных началах отсчета и полюсах.

а) Секториальная координата (ω_n) любой точки (n) при изменении начала от­счета равна секториальной координате при первом положении начала отсчета (ω'_n) минус секториальная координата нового начала отсчета (ω_m), где ω_m подставляется со своим знаком. ω_n= ω'_n - ω_m б) В случае переноса полюса из точки А₀ в точку А с координатами у_А и Z_А (рис. 43) ω_А = ω₀ – у_А· z – z_А· у + С ω_А - где секториальная координата, точки n при полюсе А; ω₀ — секториальнaя координата точки n при полюсе A₀; У_А , Z_А — координата нового полюса А при начале координат в

полюсе A₀; у, z — координаты точки n; С — произвольная постоянная, зависящая от положения начала отсчета. Например, при Z _А = Y_А = О и ω_А = ω₀ и С = 0.

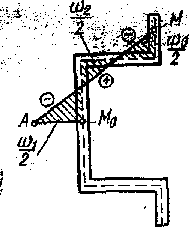
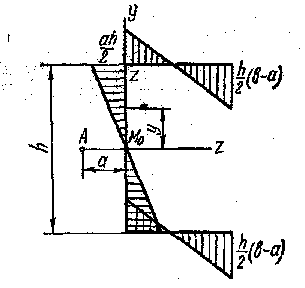
Рис.44 Рис.45

Точка М₀ принимаемая за начало отсчета, называется секториальной ну­левой точкой. Секториальная координата этой точки равна нулю. Радиус АМ₀ называется начальным радиусом. За центр отсчета (полюс А) обычно принимается центр изгиба.

Секториальная координата считается положительной, если для правой от­сеченной части стержня при взгляде со стороны сечения вдоль оси стержня она образуется поворотом радиус-вектора из начального положения по ходу часо­вой стрелки. Если радиус-вектор точки пересекает контур сечения (рис. 44), то ω определяется как алгебраическая сумма площадей разных знаков.

Секториальная координата точки М (рис. 44) ω_M= - ω₁ + ω₂ – ω₃

Наглядное представление об изменении секториальных координат точек кон­тура сечения дает эпюра секториальных координат. На рис.45 показана эпюра секториальных координат для швеллерного сечения при полюсе А и начале отсчета М₀. Эта эпюра построена путем отло­жения в точках контура их секториальных координат, которые вычисляются как: Для стенки швеллера ω_м = ± а·у Для полки швеллера ω_м = ± а· ± z·

Секториальный статический момент.

Секториальным статическим моментом площади сечения называется сумма произведений элементарных площадок на соответствующие секториальные коор­динаты. S_ω= (см⁴)

При постоянной толщине δ профиля стержня на протяжении каждого участка профиля значение S_ω можно определять по формуле S_ω = где — площадь эпюры секториальных координат участка ί .

Эпюра секториальных статических моментов может быть построена при помощи эпюры секториальных площадей.(рис.46)

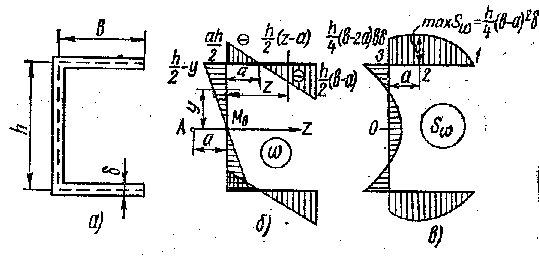
Рис.46

Пример 1.

Построить эпюру секториальных статических моментов дли швеллерного сечения (рис. 46, а) при условии, что толщина стенки и полок одинакова и равна δ. Решение. Эпюра секториальных координат при полюсе А, и начале от­счетов М₀ показана на рис. 46, б. Построение эпюры начинается из наиболее удаленных от начала отсчета точек. Значение секториальных статических моментов равно нулю в крайних точках сечения. Для сечения на расстоянии ( b— z) от края полки площадь отсеченной части эпюры секториальных координат Ω _{b— z}= [ (b - a)+ (z - a)]· (b - z)·δ = (b + z - 2a)·(b-z)·δ при z = b Ω₁=0 ; при z = a Ω_max= (b - a)²·δ ; при z = 0 Ω₃ = (b - 2a)·b·δ Для сечения стенки на расстоянии – у от точки 3 площадь отсеченной части эпюры секториальных координат = Ω₃ – ( - ay) ( - y)· δ = (b - 2a)·δ - ( - )·δ при у = (в точке 3 на стойке) Ω = Ω₃ = (b - 2a)·b·δ ; при у=0 Ω₀ = (b² - 2ab – )·δ

На основании этих данных на рис. 46, в построена эпюра S_ω. Эпюру секториальных статических моментов можно построить при по­мощи эпюры секториальных площадей точно так же, как эпюру изгибающих моментов строят по эпюре поперечных сил с использованием дифференциальных зависимостей.

Секторнально-линейные статические моменты. Секторнально-линейным статическим моментом сечения называется сумма произведений элементарных площадок на линейную и секториальную координаты.

S_ωz= (см⁵) S_ωy= (см⁵) Где и - координаты точек средней линии сечения в системе главных центральных осей.

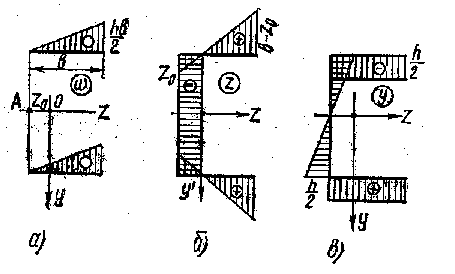
Рис. 47

Величина секториально-линейного статического момента наиболее просто определяется путем перемножения эпюр по правилу Верещагина. Например, для швеллера с полюсом в точке А значения S_ωz и S_ωy определяются следующим образом: Строится эпюра секториальных координат ω с полюсом в точке А на цент­ральной оси Z (рис. 47, а); строятся эпюры линейных координат (z , у) путем отложения расстояний точек срединной линии сечения от центральных осей ОZ (эпюра z —рис. 47, б) и ОУ (эпюра у —рис. 47, b).

Интегралы и вычисляются по правилу Верещагина путем умножения площадей эпюры ω на ординаты эпюр z или у, лежащие против центров тяжести соответствующих площадей.

Центр изгиба

В любом стержне существует такая ось, параллельная оси стержня, что силы, действующие в любой проходящей через нее плоскости, не вызывают кручения. Точку пересечения этой оси с плоскостью сечения называют центром изгиба.

Центр изгиба характерен тем, что при совмещении с ним полюса секториальных площадей секториально-линейные статические моменты сечения обра­щаются в нуль: S_ωz = S_ωy = 0.

Координаты центра изгиба определяются по формулам Y_A = ; Z_A =

где оси Z и У—главные центральные оси инерции сечения;

J _z и J _y —моменты инерции относительно этих осей.

Если сечение имеет ось симметрии, то центр изгиба лежит на этой oси. Если сечение имеет две оси симметрии, то центр изгиба лежит на пересечении осей, т. е. совпадает с центром тяжести.

Центр изгиба любого профиля, состоящего из пучка пластинок, находится в точке пересечения осей этих пластинок.

Координаты центра изгиба для сплошных незамкнутых тонкостенных про­филей, сечения которых имеют ось симметрии и могут быть разложены на эле­менты с осями симметрии, совмещенными с осью симметрии всего сечения, можно определить аналогично нахождению центра параллельных сил. С этой целью моменты инерции отдельных элементов сечения J₁, J₂ ... следует представить в виде взаимно параллельных векторов, проходящих через центры изгиба со­ответствующих элементов сечения. Тогда линия действия равнодействующего вектора J будет проходить через центр изгиба составного профиля.

Секториальные моменты инерции

Секториальным моментом инерции сечения называется сумма произведений элементарных площадок на квадраты их секториальных координат.

J _ω= dA (см⁶)

Главным секториальным моментом инерции называется секториальный момент инерции профиля, взятый относительно его центра изгиба и главной секториальной точки контура.

Главной секториальной называется точка, находящаяся на кратчайшем расстоянии от центра изгиба, для которой секториальная координата равна нулю.

В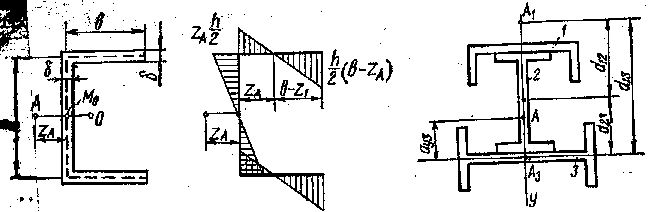 ычисление секториального момента инерции для сечений, имеющих лома­ное очертание, удобнее всего производить по способу Верещагина, построив предварительно эпюру секториальных координат с полюсом в центре изгиба и с начальной точкой в главной секториальной точке сечения. Например, для швеллерного сечения с центром изгиба в точке А и главной секториальной точ­кой М₀ эпюра главных секториальных координат имеет вид, показанный на рис. 48.

Рис. 48. ( Эп.ω ) Рис.49

Секториальный момент инерции определяется путем перемножения площадей эпюры ω на соответствующие им ординаты этой же эпюры. Для рассматриваемого сечения:

J _ω= dA = = [2(b-z_a)³ + 2 +h ]

Секториальный момент инерции составного сечения равен сумме собствен­ных секториальных моментов инерции (относительно своих центров изгиба) плюс сумма произведений осевых моментов инерции отдельных элементов, взятых по­парно, на квадраты расстояний между их центрами изгиба, деленная на осе­вой момент инерции относительно оси симметрии всего составного сечения.Например, для сечения, изображенного на рис. 49, координата центра из­гиба А, отсчитываемая от центра изгиба элемента (3), вычисляется по формуле: а_у3 = Секториальный момент инерции сечения определяется по формуле :

J _ω= J _ω1+ J _ω2+ J _ω3+

где — осевые моменты инерции отдельных элементов относительно общей оси симметрии У, — осевой момент инерции всего сечения относительно оси У; J _ω1 , J _ω2 , J _ω3 — собственные секториальные моменты инерции отдельных элементов относительно своих центров изгиба и своих глав­ных секториальных точек; d₁₂ ,d₁₃ , d₂₃ — расстояния между центрами изгиба соответствующих эле­ментов.

Секториальный момент сопротивления

Секториальный момент сопротивления сечения определяется по формуле: W_ω = (см⁴) где —секториальная координата, соответствующая одной из крайних точек контура сечения.

Пример 2. Определить положение центра изгиба и секториальный момент инерции швеллера (рис. 50, а).

Решение. Ось Z является осью симметрии швеллера. Поэтому центр изгиба лежит на оси Z .

Для определения координаты центра изгиба Z_A следует построить эпюры секториальных координат ω₀ и координат точек срединной линии у (рис. 50, в).

При построении эпюры удобно полюс А₀ взять на середине контура стенки, так как при этом эпюра будет наиболее простой (рис. 50, 6).

Координата центра изгиба Z_A =

Воспользуемся при вычислении способом Верещагина. = - 2δ₁ · · = - Момент инерции J _z = dA также можно найти, пользуясь способом Верещагина J _z = dA = 2( = (h· 6b ) Тогда координата центра изгиба Z_A = -

При одинаковой толщине стенки и полок Z_A = -

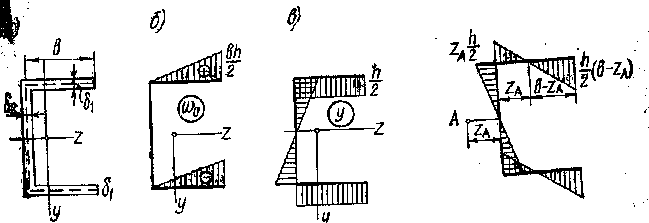Для определения секториального момента инерции сечения необходимо построить эпюру главных секториальных координат с полюсом в центре изгиба А. Эта эпюра построена на рис. 51.

Рис. 50 Рис.51

При вычислении секториального момента инерции его можно представить в следующем виде: J _ω= dA =

и воспользоваться способом Верещагина, перемножая эпюру ω саму на себя, J _ω=2δ[ ) · + = [2(b- )³+2 +h ]

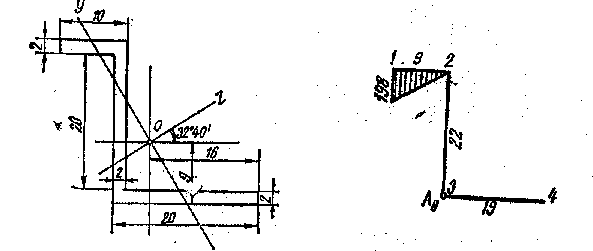
Пример 3. Определить положение центра изгиба, главной нулевой секториальной точки и главный секториальный момент инерции несимметричного сечения .(рис. 52). Положение центра тяжести сечения и главных центральных осей инерции Z и У показано на чертеже. Площадь сечения A= 100 см²; глав­ные центральные моменты инерции J _z = 10910 см⁴, J_y =1575 см⁴.

Решение. Строим эпюру секториальных площадей, принимая полюс в точке А₀ (на пересечении осей стенки и нижней полки) (рис. 53).

Координаты z и у для любой точки сечения можно определить по фор­мулам z = z₁ - y₁ ; y = y₁ z₁

Например, для точки 1

Z = —12cos32°40' —(—14)Sin32°40' = —2,54 см. у = — 14 соs 32⁰ 40' + (—12} sin 32°40' = —18,3 см. Путем аналогичных подсчетов найдем

для точки 2 Z = 5,03; у = — 13,4; для точки 3 Z = —6,85; у = +5,12; для точки 4 Z = + 8,95; у = + 15,4.

По этим данным строим эпюры z и у (рис. 54).

По эпюрам ω и Z или у, пользуясь способом Верещагина, находим секториально-линейные статические моменты сечения.

S_ωz= (13,4 + ) 2 = 29700 cм⁵.

S_ωy = (2,54 - · 1) 2 = 198 . 9 . 0,02 = 35,64 cм⁵. Рис.52 Рис.53 Координаты центра изгиба (точки А) в главных осях находим, принимая во внимание, что полюс отсчета секториальных координат (точка А₀) не совпа­дает с центром тяжести сечения О.

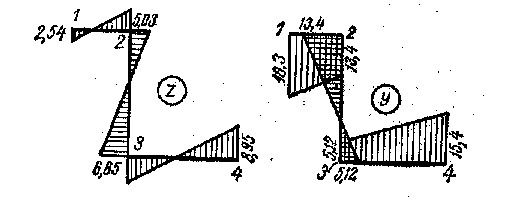Рис. 54.

Z_A = Z₀ + = - 6,58 + = - 4,13 см; y_A = y₀ + = 5,12 – = 5,10 см;

Координаты центра изгиба относительно вертикальной и горизонтальной центральных осей

Z₁ = z - y = - 4,13 ·0,482 + 5,10 ·0,540 = —0,73 см;

у₁ = у ·соs α + z· =—5,10 · 0,842 — 4,13 · 0,540 = = — 6,52 см

Найдя центр изгиба, переходим к определению главной нулевой секториальной точки. Нулевой точкой называется точка, лежащая на срединной линии контура, для которой секториальная координата равна нулю. Главной нулевой секториальной точкой называ­ется нулевая точка М₀, находящаяся на кратчайшем расстоянии от центра из­гиба. Главная нулевая секториальная точка находится из условия, что S_ω = 0.

Обозначив расстояние искомой главной секториальной точки М₀ от оси стенки сечения через t и построив эпюру секториальных площадей при полюсе в центре изгиба А, и начальном радиусе АМ₀ (рис. 54), найдем величину параметра t . S_ω = δ[ + + – ]=0 откуда 1452t – 3850 =0 следовательно t = 2,65 см

Эпюра, построенная при полюсе в центре изгиба А и начальном радиусом АМ₀, где М₀ главная нулевая секториальная точка, определяемая расстоянием t = 2,65 см, представляет собой эпюру главных секториальных координат. Эта эпюра изображена на рис. 55.

Г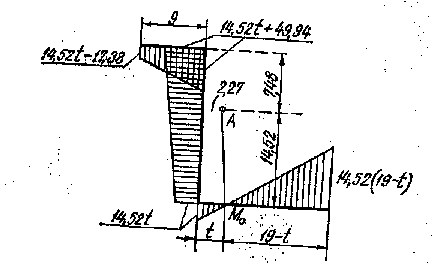 лавный секториальный момент инерции находим по эпюре главных координат, предварительно подставив значение t , применяя способ Верещагина, перемножая площади участков эпюры ω на ординаты в их центрах.

Рис.55 Эпюра ω

J _ω = = = 862 200 см⁶

3.2 Свободное кручение.

Свободное кручение стержней некруглого сечения.

Под свободным, нестесненным кручением разумеется такой вид кручения, при котором элементы скручиваемого стержня не испытывают изгиба. При кручении стержней некруглого сечения (прямоугольных, треугольных, эллиптических и др.) гипотеза плоских сечений непри­менима. Точные расчеты на кручение таких стержней могут быть по­лучены методами теории упругости. Окончательные формулы для опре­деления максимальных касательных напряжений τ_мах, относительного угла закручивания θ΄ и полного угла закручивания стержня длиной ℓ имеют вид: = ; θ΄ = (т.е. ; =

В этих формулах и — некоторые геометрические характеристи­ки, которые условно

Рис.56

называются моментом инерции и моментом сопротивления при кручении и размер­ность которых соответственно см⁴ и см³ . = αh =βh Где h - длинная и b - короткая стороны прямоугольного сечения; α , β и γ коэффициенты зависящие от отношения h⁄b приведены в таблице 2.

Таблица 2

h⁄b	1	1,5	1,75	2	2,5	3	4	6	8	10	∞
α	0,208	0,231	0,239	0,246	0,256	0,267	0,282	0,299	0,307	0,313	0,333
β	0,141	0,196	0,214	0,229	0,249	0,263	0,281	0,299	0,307	0,313	0,333
γ	1	0,859	0,82	0,795	0,766	0,753	0,745	0,743	0,742	0,742	0,743

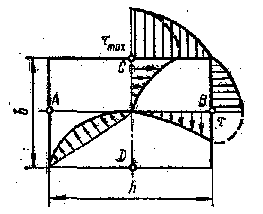
Распределение касательных напря­жений по прямоугольному сечению стер­жня приведено на рис.56 Наиболь­шие напряжения возникают в наруж­ных слоях посредине длинной стороны сечения (точки С и D). Напряжения посредине короткой стороны (в точках А и В) всегда меньше чем τ_мах и могут быть выражены через τ_мах τ = γ· τ_мах

Свободное кручение тонкостенных стержней

При кручении стержня сложного замкнутого сечения, состоящего из прямоугольных элементов, момент инерции сложного составного сечения момент инерции определяется как: = + +··· где п = 1, 2, 3, ... — номера составных простых частей сече­ния.

Так как угол закручивания для всего сечения и для каждой его части один и тот же θ΄ = = = ··· = , то крутящие моменты, воспринимаемые каждой частью сечения, пропорциональны их жесткости и последовательно определяются как:

·

·

·

Соответственно наибольшее касательное напряжение в каждом элементе сечения будет находиться в середине длинной стороны на поверхности элементов

= ( )

Очевидно, что наибольшее касательное напряжение в сечении = · )_мах

При кручении тонкостенных стержней открытого профиля (швел­лера, двутавра, уголка и других более сложных с переменной толщиной) можно воспользоваться теорией рас­чета на кручение стержней прямоуголь­ного сечения. В этом случае профиль раз­бивают на прямоугольные элементы, тол­щина δ которых значительно меньше их длины S. Согласно данным, приведенным в таблице 2 при h⁄b>10 α=β = 1/3.

Тогда для составного профиля =η ·

где η — некоторый поправочный коэффициент, учитывающий схематизацию, связанную с заменой реального профиля прямоугольниками. Ниже приведены значения коэффициента η для типичных профилей.

Сечение η

уголковое 1,00

двутавровое 1,20

тавровое 1,15

швеллерное 1,12

Наибольшее касательное напряжение при свободном кручении в сечении стержней открытого профиля определяются по формуле: = · )_мах

Эпюры касательных напряжений в любом местном сечении состоят из двух противоположно направленных параболических участков. Если заменить на каждом участке совокупность напряжений равнодействующей, и отложить эти равнодействующие во всех местных сечениях то получим поток равнодействующих касательных напряжений. Поскольку все элементы сечения объединены в одно целое, то и поток напряжений является непрерывным.