Тема 13 Балки на упругом основании.

Литература:

1. Справочное пособие по сопротивлению материалов. Рудицын. Глава 8

2. Сопротивление материалов. Смирнов. §§ с 90 по 93 включительно.

Вопросы:

1. Общие понятия о балках на упругом основании

2. Основная гипотеза

3. Упругие балки на упругом основании

   1. Бесконечно длинная балка при действии одной силы Р.

   2. Бесконечно длинная балка при действии нескольких нагрузок.

   3. Расчет коротких упругих балок.

4. Абсолютно жесткие балки на упругом основании.

1. Балкой на упругом основании называется стержень, опирающийся по всей длине на основании, деформации которого восстанавливаются после снятия нагрузки до исходного значения. Такое основание принято называть Винклеровским.

Примером балки на упругом основании может служить: длинный монолитный ленточный фундамент здания, рельс, опирающийся на шпалы (расстояние между которыми мало по сравнению с длиной рельса), монолитная бетонная облицовка каналов и так далее.

Балка на упругом основании имеет бесконечно большое количество точек соприкосновения с грунтом основания. В каждой точке балки со стороны основания действует реактивное усилие. Количество точек бесконечно велико. Т.к. уравнений равновесия для плоской системы всего три, то любая балка на упругом основании является бесконечное число раз статически неопределимой системой.

Уравнения равновесия позволяют определить суммарную реакцию со стороны основания на балку, но не дают возможности определить закон распределения этих реакций по длине балки.

2. Расчет балок на упругом (Винклеровском) основании принято вести в соответствии с гипотезой о том, что: реакция упругого основания в каждой точке пропорциональна (по закону Гука) величине просадки в этой же точке и не зависит от величин просадок соседних точек. r_x = - K ∙ y

Знак минус введен потому, что направление реакции и направление прогиба всегда противоположны. (рис.1) Здесь r_x интенсивность, распределенной по длине балки реакции. (Ед.силы/ед.длины) y - Прогиб балки в рассматриваемой точке. K - Коэффициент пропорциональности, названный в 1801 году академиком Николаем Ивановичем Фуссом - «коэффициентом постели». Коэффициент постели зависит от упругих свойств материала основания и ширины балки в рассматриваемой точке.

K=α₀ ∙b где α₀ коэффициент упругой податливости основания, b – ширина балки.

Ориентировочные значения коэффициента упругой податливости основания для некоторых видов оснований приведено в таблице.

Материал основания	α0 (кг/cм3)
Песок свеженасыпной, глина мокрая, размягченная	0,1 -0,5
Песок слежавшийся, гравий насыпной, глина влажная	0,5 - 5
Песок и гравий плотно слежавшиеся, щебень, глина малой влажности.	5 -10
Грунт песчано- глинистый искусственно уплотненный, глина твердая.	10 - 20
Известняк, песчаник, мерзлота.	20 - 100
Кирпичная кладка	400 - 500
Бутовая кладка	500 - 600
Бетон и железобетон	800 - 1500
Твердая скала	100 - 1500

2. Расчет упругих балок.

Расчетная схема балки на упругом основании загруженная произвольной нагрузкой выглядит следующим образом (рис 1).

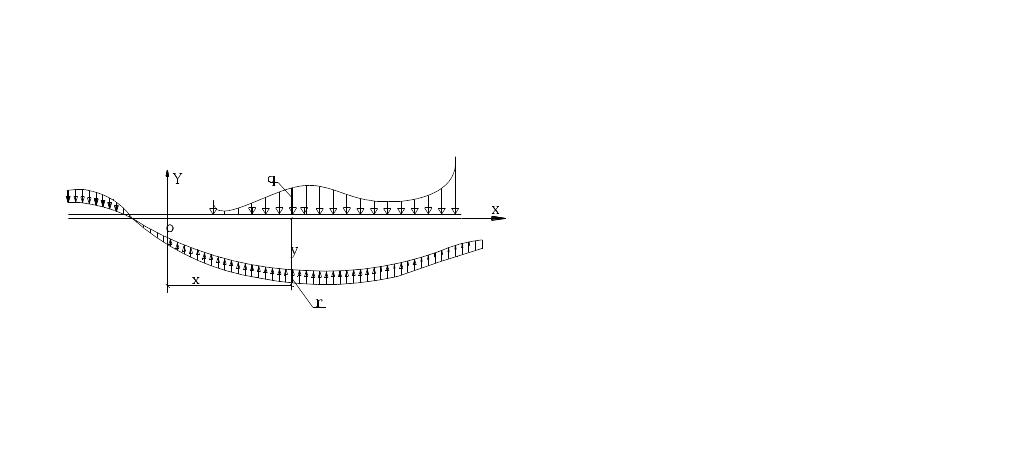
Рис. 1

Под действием произвольной распределенной нагрузки с переменной интенсивностью балка прогибается. Величина и знак прогиба переменны по длине балки. В произвольном сечении на расстоянии Х от начала координат интенсивность суммарной нагрузки на балку (Р_x) может быть определена как сумма интенсивностей активной и реактивной нагрузки.

Р_x = q_x + r_x