Экспоненциальное распределение

Непрерывная случайная функция, распределенная по экспоненциальному закону, имеет функцию распределе­ния F(x) и плотность распределения f(x) вида

(2.3)

(2.4)

Значения математического ожидания и дисперсии для экспоненциального закона распределения равны со­ответственно 1/λ и 1/ λ ².

Э

Рис 2.2. Зависимость, лежащая в основе формирования экспоненциального

распределения

кспоненциальное распределение занимает в теории массового обслуживания особое место. Это связано с тем, что распределение многих величин, таких, например, как интервалы между наступлениями соседних событий, времена обслуживания и др., во многих зада­чах массового обслуживания принимаются имеющими экспоненциальное распределение. Хотя реальные рас­пределения ( в частности распределение времени обслу­живания) часто существенно отличаются от экспоненци­ального, использование по­следнего позволяет намного упростить решение задач. Кроме того, использование экспоненциального распре­деления позволяет получить во многих случаях оценку для более напряженного ре­жима обслуживания.

Для моделирования случайных величин x_i ,имеющих экспоненциальное распределение, можно воспользоваться непосредственным решением уравнения (2.2).

Действительно, с учетом (2.4) получаем:

(2.5)

После интегрирования имеем:

(2.6)

Поскольку случайная величина (1-_i) имеет также равномерное распределение в интервале (0…1), окончательно получаем

x_i = -(1 / ) ln  _i = -  ln  _i . (2.7)

Описание алгоритма формирования значений случайной величины, распределенной по экспоненциальному закону.

1) Вводятся исходные значения: количество генерируемых величин N (не менее 100) и математическое ожидание экспоненциального закона распределения (THETA);

2) Обнуляется переменная К для подсчета количества генерируемых случайных величин;

3) Генератор псевдослучайных чисел формирует число;

4) Вычисляется случайная величина по формуле 2.7;

5) Значение величины выводится на печать;

6) Значение счётчика случайных величин увеличивается на единицу;

7) Процедура формирования случайных величин повторяется до тех пор, пока не будет получено заданное количество.

Нормальное распределение

Большое число стохастических процессов описываются нормальным распределением (законом Гаусса). Этот закон, согласно теореме Ляпунова, справедлив в случаях, когда результат (исход) процесса зависит от большого числа независимых случайных факторов, каждый из которых в отдельности влияет на результат незначительно.

Нормальный закон распределения характеризуется плотностью вероятности

(x-Mx)

1 - ———

(x) = ———— e 2 ² (2.8)

 √2

Распределение Пуассона

Распределение Пуассона нашло очень широкое применение в теории массового обслуживания для моделирования потоков событий, поскольку оно является единственным распределением, позволяющим в большинстве случаев достаточно легко получать результаты.

Потоком событий называется последовательность событий, наступающих одно за другим в случайные моменты времени. Поток событий называется пуассоновским если он удовлетворяет распределению Пуассона, является ординарным и не имеет последействия.

Дискретная случайная величина X называется распределенной по закону Пуассона, если ее возможными значениями являются 0,1,2, ... m ..., а вероятность того, что Х=т, выражается формулой

(2.9)

где а>0 — параметр закона Пуассона. Для пуассоновского потока число событий, попадающих на любой участок времени (t₀ ,t₀+τ), распределения в соответствии с выражением (2.9), причем математическое ожидание числа точек, попадающих на этот участок, равно:

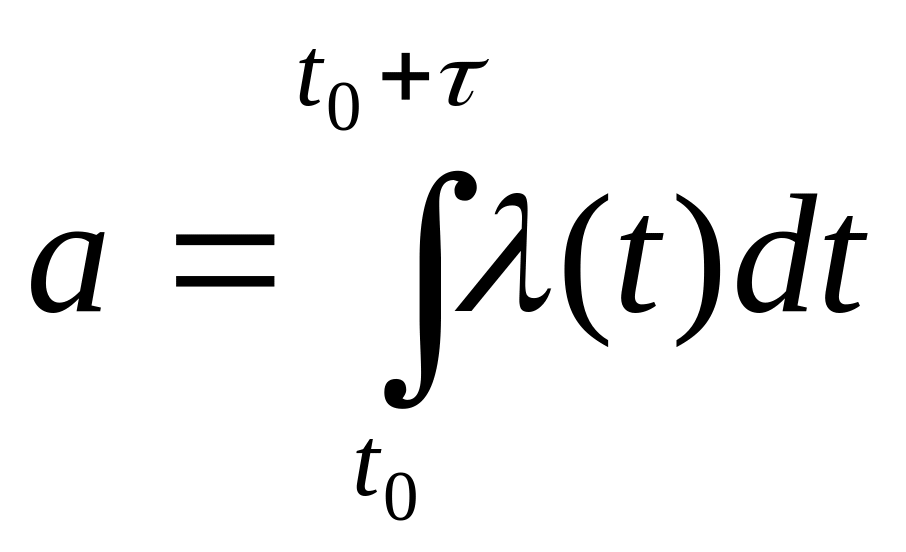, (2.10)

В последнем выражении λ(t) есть плотность потока В частности, если λ(t)=const, то пуассоновский поток называется стационарным пуассоновским или простейшим.

Для простейшего потока вероятность появления k событий за время т определяется законом Пуассона с параметром а= λτ, т. е.

(2.11)

Расстояние Т между двумя соседними событиям в простейшем потоке есть непрерывная случайная величина, распределенная по экспоненциальному закон с функцией распределения

(2.12)

Моделирование пуассоновского потока может произ­водиться двумя способами, соответствующими выраже­ниям (2.9) и (2.12). При первом способе в соответствии с заданными численными значениями вероятностей P₁ , Р₂, ..., Р_п независимых событий A₁ А₂, ..., А_п произво­дится разбиение интервала (0, 1) на п отрезков так,, чтобы длина 1-го отрезка равнялась вероятности Р,-. За­тем, выбирая из равномерного распределения в интер­вале (0, 1) случайные числа ξ_i определяют, на какой из отрезков попадает число ξ_i . Попадание случайного числа на i-й участок фиксируется как факт свершения события А_i.

Порядок выполнения работы

1. Ознакомиться с методами получения случайных величин с заданным законом распределения.

2. Получить значения 100 случайных величин, распределенных по закону Пуассона, с использованием разработанной программы на любом алгоритмическом языке.

3. Построить графики распределения плотностей вероятностей (теоретический, используя стандартные функции Excel и практические, используя свой ранее созданный генератор псевдослучайных чисел, а также стандартный встроенный генератор).

4. Оценить соответствие двух экспериментальных и теоретического распределения случайных величин.

5. Получить также значения 100 случайных величин, распределенных по нормальному закону распределения; построить графики распределения плотности вероятностей; оценить соответствие двух экспериментальных и теоретического распределения случайных величин.

6. Получить также значения 100 случайных величин, распределенных по экспоненциальному закону распределения; построить графики распределения плотности вероятностей; оценить соответствие двух экспериментальных и теоретического распределения случайных величин.

7. Сделать выводы по каждому закону распределения.

Содержание отчета

1. Название и цель лабораторной работы.

2. Задание по варианту.

3. Краткое описание и формула получения случайных величин для каждого закона распределения.

4. Последовательность 100 значений случайных величин (по 10 чисел в одной строке), полученных по всем указанным законам распределения.

5. Графики распределения плотностей вероятностей случайных величин по закону Пуассона (теоретический и два экспериментальных).

6. Графики распределения плотностей вероятностей случайных величин по нормальному закону (теоретический и два экспериментальных).

7. Графики распределения плотностей вероятностей случайных величин по экспоненциальному закону (теоретический и два экспериментальных).

8. Выводы по каждому закону распределения.

Таблица 2.

Номер варианта	Пуассоновское распределение	Экспоненциальное распределение	Нормальное распределение
		ТНЕТА()	Мх	 2
1	1,0	0,32	0,15	2,55
2	1,2	0,43	0,22	2,22
3	5,2	0,47	0,33	2,07
4	1,4	0,51	0,45	1,91
5	1,5	0,62	0,51	2,11
6	4,6	0,65	0,62	1,88
7	1,8	0,72	0,77	2,33
8	2,0	0,79	0,83	1,77
9	5,5	0,98	0,91	2,44
10	3,0	1,02	1,05	0,66
11	4,0	1,15	1,22	0,58
12	5,0	1,20	1,41	0,43
13	6,0	1,31	1,63	0,37
14	7,0	1,43	1,82	0,25
15	8,0	1,50	2,05	0,19
16	2,5	1,61	1,37	1,28
17	1,2	1,72	1,28	0,95
18	3,8	0,25	1,85	0,83
19	7,6	0,29	1,95	2,33
20	1,7	1,25	1,72	2,41
21	3,2	0,88	1,65	1,82
22	8,2	0,62	1,54	2,66
23	5,7	0,33	1,48	2,78
24	6,3	0,38	1,29	1,33
25	1,3	1,99	1,11	1,44
26	2,2	0,22	1,76	1,55
27	3,3	1,98	1,67	2,37
28	4,4	1,09	1,17	1,92
29	5,5	0,91	1,71	0,51
30	6,6	0,39	1,81	2,55