Лабораторная работа №1

Моделирование и оценка качества последовательностей

случайных чисел

Цель работы: изучить алгоритмические принципы построения генераторов псевдослучайных чисел, равномерно распределённых в интервале(0..1), и получить практические знания по оценке качества этих генераторов.

Общие сведения

Любая материальная система в реальных условиях всегда находится под воздействием внешних и внутренних факторов: возмущений и помех. Эти факторы могут быть непрерывными или дискретными, случайными величинами или функциями. При анализе функционирования таких систем возникают различные вероятностные задачи. Аналитическое решение вероятностных задач возможно только в отдельных простейших случаях, гораздо чаще приходится прибегать к моделированию функционирования сложных систем. Существует два метода решения вероятностных задач путем моделирования: детерминированный и статистический. Первый предполагает моделирование известных аналитических соотношений между вероятностными характеристиками входного воздействия и реакции системы. Задача решается путём детерминированного преобразования вероятностной характеристики воздействия в соответствующую характеристику реакции системы. Второй, статистический метод, предполагает моделирование системы, находящейся под влиянием случайных факторов. Задача решается путем статистической обработки результатов исследования модели. Система может быть линейной и нелинейной, стационарной и нестационарной. Метод является универсальным и требует моделирования соответствующих случайных факторов с заданными вероятностными характеристиками. Метод Монте-Карло – это численный метод решения математических задач при помощи моделирования случайных величин. Создателями этого метода считают американских математиков Дж. Неймана и С. Улама, применившими его к решению задач экранирования ядерных излучений. Любопытно, что теоретическая основа метода была известна уже давно. Более того, некоторые задачи статистики рассчитывались иногда с помощью случайных выборок, т.е. фактически методом Монте-Карло. Однако до появления электронных вычислительных машин этот метод не мог найти широкого применения, ибо моделировать случайные числа вручную – очень трудоёмкая работа.

Понятие «случайная величина» в обыденном смысле употребляют тогда, когда хотят подчеркнуть, что неизвестно, каким будет конкретное значение этой величины. Причем иногда за этими словами скрывается просто незнание, какова эта величина. Однако математик употребляет эти слова, вкладывая в них вполне определенное содержание. Действительно, мы не знаем какое значение примет эта величина в данном конкретном случае, но представляем, какие значения она может принимать, и знаем каковы вероятности тех или иных значений. На основании этих данных мы не можем точно предсказать результат одного испытания, но можем весьма надежно предсказать совокупность результатов большого числа испытаний.

На практике используются три основных способа генерации случайных чисел: аппаратный (физический), табличный (файловый) и алгоритмический (программный). При аппаратном способе генерации случайные числа вырабатываются специальной электронной приставкой, служащей в качестве одного из внешних устройств компьютера. Таким образом, реализация этого способа генерации не требует дополнительных вычислительных операций по выработке случайных чисел, а необходима только операция обращения к внешнему устройству (датчику). В качестве физического эффекта, лежащего в основе таких генераторов чисел, чаще всего используются шумы в электронных и полупроводниковых приборах. Однако такой способ получения случайных чисел не позволяет гарантировать качество последовательности непосредственно во время моделирования, а также повторно получать одинаковые последовательности чисел. Табличный способ предполагает наличие файла, в котором хранятся случайные числа, в оперативной памяти или на внешнем носителе. Этот способ получения случайных чисел при моделировании систем рационально использовать при сравнительно небольшом объёме файла чисел, когда для хранения можно использовать оперативную память. Хранение файла на внешнем носителе при частом обращении в процессе статистического моделирования не рационально, так как вызывает существенное увеличение затрат машинного времени при обращении к внешнему носителю. Алгоритмический способ получения последовательностей случайных чисел основан на формировании их с помощью специальных алгоритмов и программ, реализующих эти алгоритмы. Каждое случайное число вычисляется по мере возникновения потребностей при моделировании системы.

Генерирование случайных чисел

Функционирование элементов системы, подверженных случайным воздействиям, задается генераторами слу­чайных чисел, реализуемых программными методами, вырабатывающими псевдослучайные последовательности. Псевдослучайными последовательностями называют впол­не детерминированные числа, обладающие статистиче­скими свойствами случайных чисел, определяемых путем их проверки специальными тестами, а также периодич­ностью, т. е. повторяемостью через определенные проме­жутки времени.

Методы генерирования псевдослучайных чисел. При генери­ровании случайных чисел, распределенных по любым законам, в качестве задающих используют генераторы равномерно распределенных псевдослучайных чисел в интер­вале 0...1. Наибольшее распространение получили сле­дующие методы генерирования: квадратов, произведений, мультипликативный конгруэнтный и смешанный конгру­энтный методы.

Метод квадратов. В квадрат возведено теку­щее случайное число и из результатов средних разрядов выделяется следующее случайное число.

Метод произведений. Два следующих друг за другом случайных числа умножают и из произведе­ния средних разрядов выделяют следующее случайное число.

Мультипликативный конгруэнтный метод. В качестве текущего значения случайного числа выделяют остаток от деления произведения пре­дыдущего случайного числа и постоянного множителя на постоянное число.

Смешанный конгруэнтный метод. Этот метод отличается от предыдущего прибавлением к остат­ку от деления постоянного числа.

Псевдослучайные числа вычисляются с помощью рекуррентного соотношения, т.е. каждое случайное число образуется из предыдущего или нескольких предыдущих, полученных ранее Наилучшие из известных сегодня датчиков псевдослучайных чисел реализованы на основе конгруэнтных методов: линейного, смешанного и аддитивного.

Считают, что наименьшим машинным затратам и удобству дальнейших преобразований удовлетворяет последовательность случайных чисел с равномерным распределением в интервале [0, 1]. С помощью таких случайных чисел можно конструировать как случайные события с любой заданной вероятностью, так и случайные величины, обладающие практически любым законом распределения.

Основные свойства равномерного распределения

Перед тем, как перейти к рассмотрению способов составления таблиц случайных чисел с равномерным распределением, рассмотрим свойства равномерно рас­пределенной случайной величины.

Непрерывная случайная величина Х имеет равномер­ное распределение на интервале [a,b], если на этом интервале плотность распределения случайной величи­ны постоянна, а вне его - равна нулю. Закон равномер­ного распределения аналитически можно задать в виде плотности и функции распределения следующим обра­зом:

Математическое ожидание равномерного распределения находится посередине интервала [a,b]:

.

Дисперсия и среднее квадратичное отклонение соответственно равны:

; .

В силу симметричности распределения, центральный момент третьего порядка, следовательно, и коэффициент асимметрии равны нулю

.

Четвертый центральный момент

.

Коэффициент эксцесса

.

Вероятность попадания случайной величины Х на участок [a, b] интервала [a, b] определяется формулой

Примером случайной величины, имеющей равномерное распределение вероятностей, может служить ошибка при снятии показаний с измерительных приборов, если производится округление отсчета до ближайшего целого деления.

В частном случае равномерного распределения в интервале [0, 1] случайная величина Х имеет функцию плотности

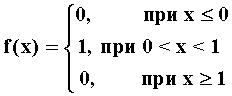
и функцию распределения

Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны

, , .

Графики плотности и изображены на рис. 1.

Рис.1.

Необходимым и достаточным условием равномерного распределения на интервале [0, 1] является следующее:

вероятность попадания случайной величины в любой подинтервал интервала [0, 1] равна длине этого подинтервала.

Из вышеизложенного ясно, что если имеется возмож­ность получать значения случайной величины X, то записанная последовательность этих значений и сос­тавит множество случайных чисел с равномерным рас­пределением.

Процесс получения значений случайной величины называют ее моделированием.

Способы генерирования равномерно распределенных случайных чисел

Рассмотрим возможные способы получения последовательностей случайных чисел с равномерным распределением, которые были использованы для составления таблиц. Примером физического генератора случайных чисел может служить урна с десятью одинаковыми карточками, на которых написаны цифры 0, 1, 2, …, 9. Если эти карточки после тщательного перемешивания в урне извлекать по одной и считывать записанную на ней цифру, возвращая карточку назад перед следующим отбором, то полученные таким образом цифры, образуют последовательность случайных чисел, равномерно рас­пределенных на множестве {0, 1, …, 9}. Записанные в виде таблицы, они представляют собой таблицу случай­ных цифр.Для получения случайных чисел может быть исполь­зован также диск, проградуированный и размеченный однозначными (от 0 до 9) либо двузначными числами (от 0 до 99). Диск приводится в движение элек­тромотором, затем резко останавливается, и оператор записывает число, на которое указывает неподвижная стрелка. Аналогичный способ (естественно в более сложном конструктивном исполнении с применением электроники) использован при составлении одной из таб­лиц случайных чисел, содержащей 1 000 000 цифр.

При расчетах на ЭВМ нерентабельно загружать оперативную память машины таблицей случайных чисел, а хранение таблицы на внешних носителях замедляет счет, так как частое обращение к внешнему запомина­ющему устройству существенно увеличивает машинное время. Кроме того, при моделировании процессов внеш­ние накопители ЭВМ загружены информацией, непосред­ственно относящейся к процессу, а алгоритм решения задачи зачастую требует еще последовательности, сос­тоящей из нескольких миллионов случайных чисел. Составление такой последовательности, запись ее на внешнюю память и частое обращение к ней снижают эффективность решения задачи.

В связи с этим возникла идея создания специального устройства к ЭВМ, генерирующего по особой команде случайные числа. При этом использовались либо собственные шумы электронных ламп, либо излучения радиоактивных веществ. Их преимущество заключается в возможности осуществления непосредственной связи с ЭВМ. Но они имеют и существенные недостат­ки: трудно проверить во время их работы равномерность распределения 0 и 1, а сбой может возникнуть из-за любых неисправностей, Кроме того, расчеты на ЭВМ обычно производятся по нескольку раз. При отладке программы по моделированию исправление ошибок зна­чительно облегчается, если ее “прогонка” производится по тем же случайным числам. Воспроизвести же те же самые случайные числа невозможно.

Чаще всего для выработки случайных чисел привлекаются генераторы, которые созданы как соответ­ствующие программы на ЭВМ. С помощью этих про­грамм по некоторому алгоритму получают последова­тельности чисел. Алгоритм построен так, что знаки 0 и 1 появляются в среднем одинаковое число раз и отсут­ствует зависимость между появлениями этих знаков и сформированными из них многозначными числами. Числа, являющиеся результатами соответствующей вычислительной процедуры в отличие от случайных чисел, получающихся при подбрасывании монеты или вытаскивании карточек из урны, называются псевдослучайными, или квазислучайными. Генераторы, созданные как соответствующие программы для ЭВМ, называются программными генераторами.

Важным достоинством программных методов является простота практической реализации. Кроме того, возможен контроль в процессе решения задачи (т.е. возможен двойной просчет). Основным недостатком всех программных методов является то, что получаемая при их реализации последовательность оказывается периодической. Поэтому очень длинные последовательности уже не будут чисто случайными. Полученные с помощью программных методов последовательности в идеале должны состоять из чисел

·        равномерно распределенных,

·        статистически независимых,

·        воспроизводимых

·        неповторяющихся.

Большинство алгоритмов для получения псевдослучайных чисел имеют вид:

,

где означает совокупность операций, которые надо проделать над числом , чтобы получить .

Например, широко известные способы имитации равномерно распределенных случайных чисел основаны на реализации рекуррентного соотношения

_(1.1)

и определяет как наименьший неотрицательный вычет по модулю m (т.е. остаток от деления на m). Это разностное уравнение описывает динамику инерционной нелинейной дискретной системы, автоколебания в которой стабилизированы механизмом квантования. Причем процесс во многом определяется выбором начальных значений х_0-1,…, х_0-r. В зависимости от того, является ли функция j линейной или нет, различают линейные и нелинейные методы. Наиболее распространенный алгоритм для получения равномерно распределенных псевдослучайных чисел был предложен Д. Лемером. В алгоритме Лемера задаются двумя соответствую­щим образом подобранными целыми числами: множи­телем и модулем . Последовательность случайных чисел вычисляется следующим образом:

1) число известно с предыдущего шага. Вычисля­ется произведение ,

2) число делится на . Получается целое чис­ло и целочисленный остаток , что можно предста­вить в виде:

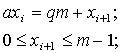
3) так как - число между 0 и , то нужно его еще разделить на , чтобы получить число между 0 и 1:

.

Т.о., соотношение (1.1) записывается в виде

. (1.2)

При этом говорят, что числа и сравнимы по модулю , т.е. они являются равно остаточными при делении на . Формулу (1.2) называют сравнением по модулю, а остаток - наименьшим положительным вычетом по модулю . Этим объясняются оба названия алгоритма - метод мультипликативного сравнения или метод вычетов.

Последовательности случайных чисел, полученные методом мультипликативного сравнения, периодически повторяются. Это связано с тем, что числа могут принимать только значения 0, 1, 2, …, . Итак, самое большее через шагов уже один раз полученное число должно появиться опять, а за ним повторяется и вся последовательность. Таким образом, длина периода при модуле не может превышать .Это означает, что на практике можно обеспечить удовлетворительную величину периода, если выбирать модуль m достаточно большим. Статистические свойства последовательности зависят от выбора и . Выбор не зависит от системы счисления, а только от длины машинного слова. Так для 32 разрядного машинного слова можно выбрать и множитель . Число является простым. В этом случае достигается максимально возможная длина периода , т.е. .

Наиболее часто применяемые в настоящее время генераторы равномерно распределенных случайных величин в общем виде можно представить таким образом:

,

(1.3)

где , , …, , и , а также получаемые числа x₁, x₂, … являются целыми числами. В этом случае можно получить более длинные периоды в последовательности по сравнению с методом вычетов. Числа в получающейся последовательности имеют слабую корреляцию.

Образование равномерно распределенных чисел на интервале [0, 1] можно представить так:

.

(1.4)

Генераторы этого вида называются линейными (конгруэнтными). Рассмотренный выше пример получения случайных последовательностей методом мультипликативного сравнения является частным случаем линейного генератора. Подставляя в (1.3) и положив, что , получим:

.

(1.5)

Генератор вида (1.5) называется мультипликативным. На практике он обладает достаточно хорошими статистическими характеристиками.

Если в (1.3) положить , , а , то получим выражение для смешанного генератора

.

(1.6)

И наконец если в (1.3) положить и , то генератор такого вида называется аддитивными или генератором Фиббоначи:

.

(1.7)

Генератор вида (1.3), где все , называется обобщенным аддитивным генератором или обобщенным генератором Фибоначчи.

Например, рассмотрим смешанный генератор:

1255*135+10555 (mod 1000) = 179980 (mod 1000) = 980

1255*980+10555 (mod 1000) = 1240455 (mod 1000) = 455

Таким образом, по целым числам последовательности {х_i} можно построить последовательность {х_i/m} рациональных чисел из единичного интервала. Например, 0,98; 0,455 и т.д.

Удобными и экономичными являются алгоритмы, требующие выполнения лишь операций сдвига и сложения. Так для десятичных чисел используют следующий алгоритм:

где  – не кратно 2 и 5;

n - число десятичных цифр в машинном слове.

Максимальный период равен . Кроме того, в этом случае

-       во-первых, вычисление остатка от деления сводится к выделению n младших разрядов делимого;

-     во-вторых, преобразование целого числа в рациональную дробь из интервала [0, 1] осуществляется подстановкой слева от него десятичной запятой. Таким образом, из процесса исключаются две операции деления.

Вполне удовлетворительные для практики результаты дают следующие программные способы получения псевдослучайных чисел.
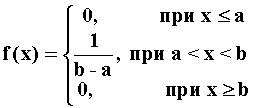
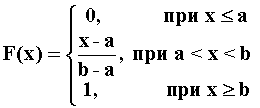