1.4. Математические предложения

Взаимосвязи между объектами и свойствами выражаются с по­мощью предложений. Предложения могут быть сформулированы при помощи слов и записаны при помощи математических символов:

«У квадрата все стороны равны», «5<7» и др.

Каждое математическое предложение характеризуется содер­жанием и логической структурой. По структуре различают элемен­тарные и составные предложения.

Элементарные предложения:

1) 20 — четное число,

2) х>8

3) л=7

Составные предложения:

1) 20 — четное и делится на 5,

2) х ≥8,

3) х7.

Составные предложения образуются из элементарных с по­мощью союзов «и», «или», частицы «не» и др. Эти слова называются логическими связками.

Примеры составных предложений различных по структуре при­ведены на рисунке 8:

Составное предложение	Логическая структура	Элементарное предложение А	Элементарное предложение В
20 — четное и де­лится на 5	А и В	20 четное число	20 делится на 5
х ≥8	А или В	х >8	х=8
х7	Не А	х=7	—

Рис.8

Задание 5

Определите структуру предложений и выявите в них элементар­ные предложения:

- «Параллельные прямые не пересекаются»;

- «Противоположные стороны прямоугольника параллельны и равны»;

- «Число оканчивается нулем или пятеркой».

1.5. Высказывания и высказывательные формы

При формулировке или чтении любого предложения нас инте­ресует, истинно оно или ложно, то есть его значение истинности.

Задание 6

Выберите предложения, к которым можно задать вопрос, истинно оно или ложно:

а) 6 • 6=36; г) х+4>3;

б) 7 • 7=47; д) 0 — число натуральное;

в) х+100=5; е) а||b.

Очевидно, что не ко всем предложениям можно задать вопрос о его истинности. Среди предложений выделяют высказывания и вы­сказывательные формы.

Высказывание — предложение, относительно которого имеет смысл вопрос, истинно оно или ложно.

Высказывательная форма — это предложение, которое содержит одну или несколько переменных и обращается в высказывание при подстановке в него конкретных значений переменных.

Примеры:

6 • 6 = 36 — истинное высказывание;

7 • 7 = 47 - ложное высказывание;

х+100=5 — высказывательная форма; если х= -95, то данная высказывательная форма обращается в истинное высказывание; если х=95, то данная высказывательная форма обращается в ложное высказывание.

Задание 7

Определите, какие из следующих записей являются высказы­ваниями, какие высказывательными формами:

а) 13-5=9; г) х+4;

б) (23+7)—10; д) 5 — число натуральное;

в) х +2=5; е) у — число четное.

Высказывания и высказывательные формы бывают элементар­ными и составными. Составные предложения могут образовываться при помощи логических связок «и», «или», «не» и др.

В элементарных высказываниях истинность устанавливается по содержанию. Например, предложение «число 20 четное» — истинное высказывание, так как нам известно, что 20:2=10, а предложение «5+2=8» — ложное высказывание, так как мы знаем, что 5+2=7.

Для определения истинности составного высказывания надо выявить его структуру и определить значение истинности элемен­тарных предложений, его составляющих.

Рассмотрим такие виды составных высказываний: «А и В», «А или В», «Не А», где А, В - элементарные высказывания. Значение истинности таких предложений можно определить по таблице ис­тинности, которую нетрудно заполнить самостоятельно, выполнив задание 8.

Задание 8

Ребенку задают вопросы:

— Назови число, кратное 3 и 7.

- Назови число, которое делится на 5 или на 6.

— Назови нечетное число.

Придумайте различные варианты детских ответов, установите их зна­чение истинности. Выявите структуру получившихся предложений и заполните таблицу истинности.

Предложение вида «А и В» истинно, когда истинны оба элемен­тарных предложения, и ложно, когда ложно хотя бы одно из элемен­тарных предложений.

Иногда вместо союза «и» используются слова: «а», «но», «одна­ко», «не только ..., но и ...», которые имеют тот же смысл.

Предложение вида «А или В» истинно, когда истинно хотя бы одно из элементарных предложений, и ложно, когда ложны оба элемен­тарных предложения.

Связка «или» в математике не является разделительной, поэтому предложение «А или В» истинно, если истинны оба высказывания.

Предложение вида «Не А» истинно, когда элементарное предложе­ние А ложно, и ложно, когда А — истинно.

Вместо частицы «не» можно использовать слова «неверно, что...».

Зависимость значения истинности составных предложений от их структуры и истинности элементарных предложений, их состав­ляющих, можно представить в виде таблицы, изображенной на ри­сунке 9.

А	в	Аи В	А или В	Не А
И	и	И	И	Л
и	л	л	И	—
л	и	л	и	И
л	л	л	л	—

Р ис. 9

В работе с детьми дошкольного возраста уже используют зада­ния, требующие логических рассуждений. Примеры: 1) Наглядный материал изображен на рисунке 10.

Задание ребенку: «Возьми черный треугольник». Выбрав фигу­ру, ребенок формулирует вслух или подразумевает предложение: «Вот черный треугольник», что другими словами значит: «Данная фигура черного цвета и является треугольником». Выявим логичес­кую структуру этого высказывания и содержание элементарных ма­тематических предложений, входящих в состав этого высказывания.

Структура: «А и В»; элементарные предложения: А — «Данная фигура черного цвета», В — «Данная фигура — треугольник».

Выбор ребенка оценивается воспитателем, исходя из правил ло­гики, что отображено на рисунке 11.

2) Наглядный материал изображен на рисунке 12.

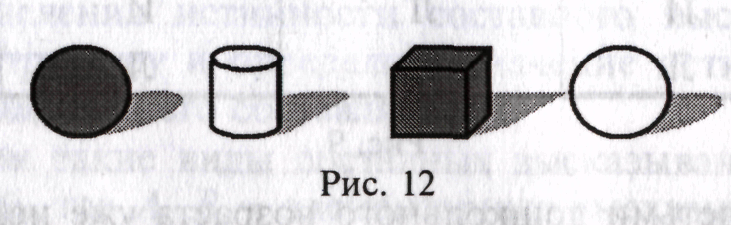
Задание ребенку: «Возьми фигуру, похожую на яблоко по цвету или по форме». Свой выбор ребенок сопровождает словами (или их подразумевает): «Вот фигура, похожая на яблоко по цвету или по форме». Выявим логическую структуру этого высказывания и содер­жание элементарных математических предложений, входящих в состав этого высказывания.

Структура: «А или В»; элементарные предложения: А — «Фигура, имеет цвет как у яблока», В — «Фигура имеет форму как у яблока».

На рисунке 13 отражена зависимость оценки действия ребенка от его выбора, где также выполняются правила логики.

3) Наглядный материал изображен на рисунке 14.

Задание ребенку: «Выбери лишнюю фигуру, объясни, почему ты так думаешь». Ребенок выполняет задание и объясняет свой выбор: «Вот эта (называет) фигура — лишняя. Все фигуры — многоугольни­ки, а она — не многоугольник». По сути дела, ребенок формулирует высказывание структуры «Не А», где элементарное предложение:

Выбор ребенка	Значение истинности элементарного предложения А	Оценка действия
О	Л	«правильно»
Л	И	«неправильно»

Рис. 15

А — «фигура является многоугольником», составное предложение: «Не А» — «фигура не является многоугольником».

Взаимосвязь оценки воспитателя и выбора ребенка можно уви­деть на рисунке 15.

Если предложение А — элементарное высказывание, то для по­строения отрицания следует либо предварить его словами «неверно, что...», либо поставить частицу «не» перед сказуемым (если А содер­жит частицу «не», то отбросить ее).