Тема 1 элементы логики

1.1. Объем и содержание понятия

Всякий математический объект обладает определенными свой­ствами. Например, квадрат имеет четыре стороны, четыре прямых угла и др. Различают свойства существенные и несущественные.

Существенное свойство - свойство, без которого объект не мо­жет существовать.

Несущественное свойство - свойство, отсутствие которого не влияет на существование объекта.

Для квадрата, изображенного на рисунке 1, существенные свой­ства: AB=BC=CD=DA, AB||DC, AD||BC; несущественные свойства: АВ, DC — горизонтальны, AD, ВС — вертикальны.

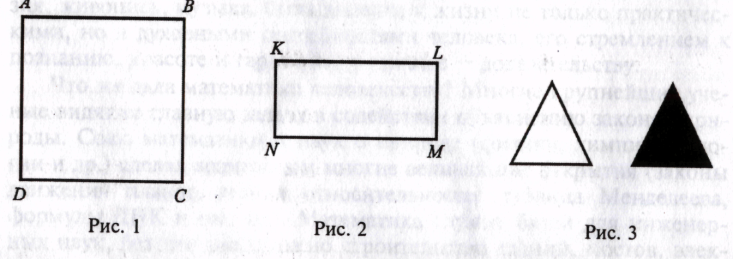Е сли квадрат повернуть, сохранятся только существенные свой­ства, именно они и составляют понятие об объекте.

Задание 1

Назовите существенные свойства фигуры, изображенной на рисун­ке 2.

Рассмотрим пример диалога с дошкольником, используя на­глядный материал (рис. 3):

— Опиши левую фигуру. (Белый треугольник.)

— Опиши правую фигуру. (Черный треугольник.)

— Чем фигуры похожи? (Формой.)

— Чем фигуры отличаются? (Цветом.)

— Что есть у треугольника? (3 стороны, 3 угла.)

Таким образом, дети выясняют существенные и несуществен­ные свойства понятия «треугольник». Существенные свойства: «иметь три стороны», «иметь три угла»; несущественное свойство т цвет.

Содержание понятия — совокупность всех существенных свойств объекта.

Когда говорят о математическом объекте, имеют в виду всю со­вокупность объектов, обозначаемых одним термином.

Объем понятия — совокупность всех объектов, обозначаемая одним термином.

Например, содержание понятия «квадрат» — это совокупность всех существенных свойств, которыми обладают квадраты, а в объ­ем этого понятия входят все квадраты, которые только можно пред­ставить.

Итак, любое понятие характеризуется:

— термином (название);

— объемом;

— содержанием.

1.2. Отношение рода и вида между понятиями

Математические понятия могут находиться в разных отноше­ниях.

Понятия находятся в отношении рода и вида, если объем одного понятия включает объем другого понятия, но не совпадает с ним.

Примеры:

1) Квадрат и прямоугольник находятся в отношении рода и вида, где прямоугольник — родовое понятие, а квадрат — видовое поня­тие, так как все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.

2) Отрезок и прямая не находятся в отношении рода и вида, так как отрезок — это часть прямой, а не ее разновидность. Они нахо­дятся в отношении части и целого.

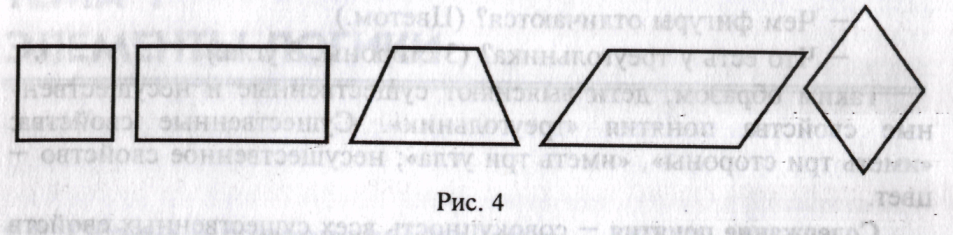
Уже в дошкольном возрасте дети рано начинают понимать ро­довидовые отношения, не называя их явно. Например, выполняя задание: «Назови одним словом» (рис. 4), они подразумевают, что понятия «квадрат», «прямоугольник», «трапеция», «ромб», «параллелограмм» являются видовыми по отношению к понятию «четырехугольник».

Если объемы понятий совпадают, то эти понятия тождественны.

Например, понятия «равносторонний треугольник» и «равно­угольный треугольник» тождественны. В школе на уроках русского языка дети изучают понятие «синонимы» — слова, различные по звучанию, но тождественные по смыслу.

Некоторые особенности родовидовых отношений между понятиями

1) Понятия рода и вида относительны. Одно и то же понятие мо­жет быть родовым по отношению к одному понятию и видовым по отношению к другому. Например: понятие «прямоугольник» — ро­довое к понятию «квадрат», но видовое к понятию «четырехуголь­ник».

2) Для данного понятия часто можно указать несколько родовых понятий. Например, для понятия «квадрат» родовыми являются по­нятия «прямоугольник», «ромб», «четырехугольник», «многоуголь­ник», «геометрическая фигура».

3) Видовое понятие обладает всеми свойствами родового понятия. Например: квадрат обладает всеми свойствами прямоугольника.

4) Если два понятия находятся в отношении рода и вида, то между их объемами и содержаниями существует взаимосвязь: если объем больше, то содержание меньше, и наоборот. Например, объем понятия «прямоугольник» больше, чем объем понятия «квадрат», так как все объекты второго понятия являются и объектами первого понятия. Содержание понятия «прямоугольник» меньше, чем содер­жание понятия «квадрат», так как квадрат обладает всеми свойства­ми прямоугольника и еще другими свойствами, присущими только ему.

Задание 2

Назовите, какие из перечисленных понятий находятся в отношении рода и вида: круг, ломаная, треугольник, отрезок, многоугольник, радиус, окружность.