
- •Кафедра “Электропривод и автоматизация промышленных установок”
- •02 Февраля 2012г., протокол №6. Белорусско-российский университет
- •1 Цель работы.
- •2 Основные теоретические сведения
- •2.1 Основные уравнения трансформатора
- •3 Задание на выполнение лабораторной работы.
- •3.1 Записать паспортные данные трансформатора в отчет.
- •3.2 Записать паспортные данные измерительных приборов в таблицу 1.
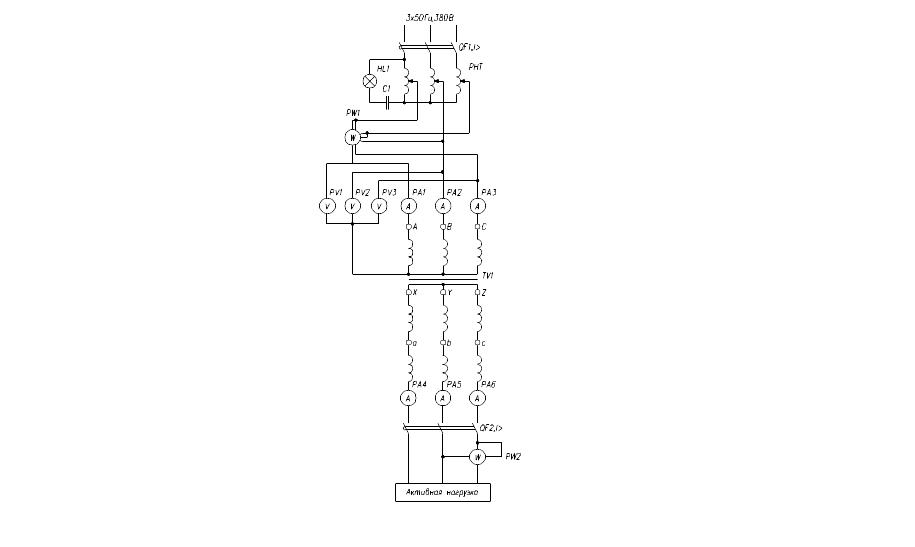
- •3.3 Ознакомиться со схемой и порядком включения стенда.
- •3.4 Определить коэффициент трансформации.
- •3.8 Сделать обработку полученных данных. Провести анализ результатов лабораторной работы и составить подробный отчет.
- •4 Порядок работы с лабораторной установкой.
- •4.1 Определение коэффициента трансформации
- •4.2 Опыт холостого хода трансформатора.
- •4.3 Опыт короткого замыкания.
- •4.4 Исследование трансформатора под нагрузкой
Министерство образования Республики Беларусь
Министерство образования и науки Российской Федерации
Федеративное агентство по образованию
Государственное учреждение высшего профессионального образования
«Белорусско-Российский университет»
Электротехнический факультет
Кафедра “Электропривод и автоматизация промышленных установок”

Методические указания к лабораторной работе
по курсу “Электрические машины”
Для студентов специальности 1-53 01 05
“Автоматизированные электроприводы”
Лабораторная работа № 6
“Исследование трехфазного трансформатора ”
Могилев 2012
УДК 621.313 Составитель: Лапицкий В.А.
Кольцов С.В.
Методические указания к лабораторной работе №6 “Исследование трехфазного трансформатора” по дисциплине «Электрические машины». Для студентов специальности 1-53 01 05 “Автоматизированные электроприводы”
Методические указания рассмотрены и одобрены на заседании кафедры “Электропривод и АПУ”
02 Февраля 2012г., протокол №6. Белорусско-российский университет
Р
PV4

1 Цель работы.
Ознакомиться с устройством трансформатора.
Усвоить практические приемы лабораторного исследования трехфазного трансформатора методом холостого хода, короткого замыкания и под нагрузкой.
2 Основные теоретические сведения
Трансформатором называется статический электромагнитный аппарат, предназначенный для преобразования одной - первичной - системы переменного тока в другую - вторичную - той же частоты, имеющую в общем случае другие характеристики, в частности, другое напряжение и другой ток.
Работа трансформатора основывается на принципе электромагнитного взаимодействия двух или, в общем случае, любого числа контуров, неподвижных относительно друг друга. Если к первичной обмотке подвести напряжение U1, от сети переменного тока, то в обмотке возникает ток I1, который создает синусоидально изменяющийся магнитный поток Ф, замыкающийся по сердечнику.
Поток Ф индуктирует Э.Д.С. как в первичной, так и во вторичной обмотке. При подключении ко вторичной обмотке трансформатора нагрузки R в этой обмотке возникает ток I2, и на ее зажимах устанавливается некоторое напряжение U2. Результирующий магнитный поток сердечника Фс создается током обеих обмоток.
2.1 Основные уравнения трансформатора
Пусть u1 - мгновенное значение напряжения, подводимого к первичной обмотке; i1 и i2 - мгновенные значения токов в первичной и вторичной обмотках.
Тогда, если первичная обмотка имеет W1 витков, а вторичная W2, то в обмотках создается намагничивающаяся сила соответственно i1 W1 и i2 W2.
i1 · 1 + i2 · 2 = i0 · 1; (1)
i1 · 1 = -i2 · 2 + i0 · 1; (2)
где i0·1 - намагничивающая сила, создающая в сердечнике поток, мгновенное значение которого Фt.
Это основной поток, он распределяется практически равномерно по сечению сердечника трансформатора и сцепляется со всеми витками как первичной, так и вторичной обмоток.
Основной поток создает э.д.с. в первичной и вторичной обмотках:
e1=-W1·=-; (3)
e2=-W2·=-; (4)
где 1 и 2 - потокосцепления, соответствующие только основному потоку Фt.
Кроме основного потока, в трансформаторе присутствуют потоки рассеяния Фб1 и Фб2, которые создают э.д.с. рассеяния:
eб1=-Lб1·; (5)
eб2=-Lб2·; (6)
По второму закону Кирхгофа запишем уравнение э.д.с. в первичной обмотке:
u1+e1+eб1=i1·r1; (7)
где r1 - активное сопротивление первичной обмотки.
u1=-[e1+eб1+(-i1·r1)]; (8)
Для вторичной обмотки:
u2=e2+eб2+(-i2·r2); (9)
Подставив в уравнения (8), (9) значения э.д.с. и учитывая, что:
1 =L1 · i1+M12 · i2; (10)
2=L2 · i2+M21 · i1; (11)
M12=M21=M; (12)
Получим:
U1=L1·+M·+i1·R1; (13)
0 =L2·+M·+i2·r2+u2; (14)
где L1 и L2 - полные индуктивности первичной и вторичной обмоток;
М - взаимоиндуктивность обмоток.
Если напряжения, э.д.с. и токи представляют собой синусоидальные функции времени, то действующие значения этих функций можно изобразить в комплексной форме U, E и I. Тогда, проводя необходимые преобразования, можно записать уравнения (13) , (14) в виде:
U1=jwL1·I1+jwM I2+I1·r1=E1+I1·Z1; (15)
0=jwL2·I2+jwM·I1+I2·r2+U2=E2-I2·Z2−U2; (16)
Математический анализ процессов, протекающих в трансформаторе, значительно упрощается, если параметры одной из обмоток (обычно вторичной) привести к числу витков другой обмотки (первичной). Для этого пересчитывают вторичную обмотку, имеющую число витков W2, на эквивалентную ей приведенную обмотку, имеющую такое же число витков W1, как и первичная обмотка. Тогда уравнения напряжения и ЭДС примут вид:
U1=-E+I1·Z1; (17)
E-I·Z=U; (18)
или
E=E1=I·Z+U; (19)
Коэффициентом трансформации называется отношение э.д.с., наводимых в первичной и вторичной обмотках трансформатора основным магнитным потоком Ф.
K= =
 =
; (20)
=
; (20)
Зная величину коэффициента трансформации, можно определить основные параметры вторичной цепи трансформатора:
U2= ; (21)
I2=I1·K; (22)
За последние десятилетия значительно возросли единичные мощности и рабочие напряжения трансформаторов при уменьшении конструкционных материалов, повысился их к.п.д., достигнув у наиболее мощных трансформаторов 99,7%.
В результате этого резко уменьшились вес и габариты трансформаторов.
