Задание 7 Формирование сплайн–интерполяторов расчетных и экспериментальных данных. Интерполирование границы устойчивости сау с периодической нелинейностью «в большом»

7.1. Вставьте в РДМ текстовый блок:

«Задание 7

Текущая дата. Сплайн – интерполяция данных.

7.1. Интерполяция в точках границы устойчивости»

• Используя точки границы, найденные в п. 6.3 задания 6, постройте интерполяционную кривую границы устойчивости ic(q) на основе разд. 8.1. Пособия с использованием кубического сплайна cspline(…).

• Скопируйте рисунок из п.6.3 задания 6. Нанесите на нем интерполяционную кривую ic(q). С помощью 2-кратного применения панельки Zoom покажите степень совпадения исходной и интерполяционной границ.

• Вычислите затухания в 3 любых точках границы (в начале, в середине и в конце, не являющихся точками интерполяции) по интерполяционной зависимости ic(q), аналогично рис. 8.1, В Пособия.

7.2. Вставьте в рабочий документ текстовый блок «7.2. Исследование точности сплайн – интерполяции кубическими сплайнами: lspline(…),рspline(…) и сspline(…). Вариант №___»

• Для пробной функции (см. ваш вариант в табл. 15.9.1 разд. 15.9) постройте график f(х) в промежутке х и c шагом , указанных в графах 4 и 5 таблицы. Для интерполяционного диапазона х из табл. 15.9.1 (графа 3) составьте векторы vха и vуa интерполяционных значений переменной х,и f(х) в точках начала и конца диапазона и в таких, которые приближенно соответствуют максимумам и минимумам f(х) (Для измерения точек используйте панельку Trace; см. также рис. 8.2 и 8.3 Пособия). Напишите выражение для интерполяционного вектора vs вторых производных в интерполяционных точках для трех видов сплайнов: vsL, vsp и vsc.

• Для интерполяционных точек из п.а) сформируйте 3 интерполяционных сплайна iL(х), ip(х), ic(х) (см. рис. 8.2, Б), и по методике рис. 8.3 Пособия на рисунке с f(х) постройте их графики, а также график vха(vуa).

• Выделите участки с наибольшими отклонениями сплайнов от пробной функции f(х) в пределах заданного в табл. 15.9.1 диапазона интерполяции х (должно быть не менее 2), измерьте эти отклонения и составьте по результатам таблицу, аналогичную табл. 8.2 из Пособия. Вычислите относительную погрешность интерполяции (х) = макс.откл./ f(х) .

• Если погрешность (х)  10…20 %, то на таких участках х вставьте дополнительное число точек интерполяции, чтобы погрешность не превышала допустимого уровня.

Удостоверьтесь по графикам вашего рисунка, что близость интерполяционной функции к исходной реализуется только в пределах интерполяционного диапазона.

Задание 8 Минимизация линейной и квадратичной целевых функций шести и пяти аргументов при типовых ограничениях

1. Вставьте в РДМ текстовый блок:

«Задание 8

Текущая дата. Вычисление максимума (минимума) целевой функции

8.1. Вычисление оптимума линейной целевой функции. Вариант №___»

8.2. Ознакомьтесь с разд. 11.1 и 11.2 разд. 11 Пособия «Вычисление максимума (минимума) функции».

8.3. Меняя состав операционного (виды ограничений) блока и тип оптимизации, найдите решения задач линейного программирования в следующей постановке.

Необходимо определить 6-компонентный вектор х, оптимизирующий линейную функцию

у13(х) = f1х1+f2х2+f3х3 +f4х4 +f5х5 +f6х6, (8.1)

при комбинации следующих ограничений:

a11 х1+a12 х2+a13 х3+a14 х4+a15 х5+a16 х6  b1,

a21х1+a22 х2+a23 х3+a24 х4+a25 х5+a26 х6  b2 ,

a31х1+a32 х2+a33 х3+a34 х4+a35 х5+a36 х6 b3,

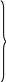
a41х1+a42 х2+a43 х3+a44 х4+a45 х5+a46 х6 b4, (8.2)

a51х1+a52 х2+a53 х3+a54 х4+a55 х5+a56 х6 b5,

a61х1+a62 х2+a63 х3+a64 х4+a65 х5+a66 х6 b6,

c11 х1+c12 х2+c13 х3+c14 х4+c15 х5+c16 х6 = d1,

c21 х1+c22 х2+c23 х3+c24 х4+c25 х5+c26 х6 = d2, 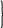(8.3)

c31 х1+c32 х2+c33 х3+c34 х4+c35 х5+c36 х6 = d3

и заданной области поиска:

на х не налагается дополнительных ограничений, (8.4)

все компоненты х больше нуля, (8.5)

х1 g1 , х2 g2 , х3  g3 , х4 g4 , х5  g5 , х6  g6. (8.6)

Численные значения коэффициентов  в вашем варианте исходных данных к заданию 8 – разд. 15.9.2, табл. 15.9.1 .

8.3.1. Сформируйте в РД исходные данные (8.1)…(8.6) в векторно-матричном виде (см. рис. 11.2 Пособия, этапы 1…5).

8.3.2. Ниже векторно-матричного представления:

• Сформируйте все ограничения, которые будут участвовать в процессе оптимизации цельфункции у13(о1) – этапы 6 и 7 рис. 11.2, А.

• сформируйте максимизатор, аналогичный показанному на рис. 11.2, Б Пособия, с выводом вектора о1 и цельфункции у13(о1) – рис. 11.2, В и Г;

• скопируйте ограничения и максимизатор и вставьте их ниже вектора о1 и цельфункции у13(о1) и

сфор­мируйте из него второй минимизатор, с заменой maximize(…) на minimaize(…), о1 на о2 и с выводом вектора о2 и функции у13(о2).

8.3.3. Вставьте в ваш Уорд-файл «Фамилия-MCad.doc» пункт «8.1. Текущая дата. Вычисление максимума (минимума) линейной целевой функции решателем Linear».

В этом пункте сформируйте таблицу, аналогичную табл.8.1 с тем же названием, графы 6…9 которой следует заполнить результатами расчетов х_опт и у13(х_опт) из первого и второго оптимизаторов из п. 8.3.2.

8.3.4. Найдите оптимальные значения х и у(х) для задач с сочетанием ограничений и согласно табл. 8.1 («+» - ограничение есть, «-» – ограничение отсутствует), путем перемещения в оптимизатор мышкой или удаления из него блоков ограничений типа (11.6) из Пособия. При отсутствии решения в соответствующие ячейки таблицы вставьте фразу «Нет решения».

Таблица 8.1

Оптимизация линейной цельфункции у13(х) при сочетании различных ограничений

№ задачи	Ограничения-неравенства ах  b**)	Ограничения-равенства сх = d	Область поиска		Минимзация у13(х)		Максимизация у13(х)
			х  0	х  g
					х мин	у13(х) мин	х мах	у(х) мах
	+*)	–*)	–	–
	+	–	–	+
	+	–	+	+
	+	–	+	–
	+	+	–	–
	+	+	–	+
	+	+	+	+
	+	+	+	–
	–	–	+	–
	–	+	–	–
	–	+	–	+
	–	+	+	+
	–	+	+	–
	–	–	+	+
	–	–	–	+

Примечание к табл. 8.1

*) «+» - ограничение есть, «–» – ограничение отсутствует.

**) Ограничения-неравенства представлены в матрично-векторном виде.

8.4. Вставьте в РДМ текстовый блок «8.2. Текущая дата. Вычисление максимума (минимума) квадратичной целевой функции. Вариант №___».

8.5. Ознакомьтесь с разд. 11.1 и 11.3 разд. 11 Пособия «Вычисление максимума (минимума) функции».

8.6. Меняя состав операционного блока (виды ограничений) и тип оптимизации, найдите решения задач квадратичного программирования в следующей постановке.

Необходимо определить 5-компонентный набор переменных х0,…,х4, оптимизирующий функцию

у17(х0,…,х4) = m00х0²+m11х1² +m22х2²+m33х3² +m44х4² + m01х0х1 + m02х0х2+ m03х0х3+ m04х0х4 + +m12х1х2 + +m13х1х3 + + m14х1х4 + m23х2х3 + m24х2х4+ m34х3х4 +а0х0+ а1х1+ а2х2 + а3х3 + а4х4, (8.7)

(вариант значений коэффициентов выражений (8.8) … (8.12) - см. табл. 15.10.2 - 15.10.5 в разд. 15.10.2 при комбинации следующих ограничений:

линейных неравенств:

c00х0 +c01х1+c02х2 +c03х3 +c04х4  b0 ,

c10х0 +c11х1+c12х2 +c13х3 +c14х4  b1 , (8.8)

c20х0 +c21х1+c22х2 +c23х3 +c24х4  b2 ;

линейных равенств:

cе00х0 +cе01х1+cе02х2 +cе03х3 +cе04х4 = bе0 ,

(8.9)

cе10х0 +cе11х1+cе12х2 +cе13х3 +cе14х4 = bе1 ;

область изменения переменных х:

1. на х не налагается ограничений, (8.10)

2. все переменные х больше нуля, (8.11)

3. х0 u0, х1 u1, х2  u2 , х3  u3 , х4  u4 . (8.12)

нелинейные неравенства cn(x0,…,x4)  0:

C_n00x0ⁿ¹+ C_n01x1ⁿ² + C_n02x2^1.6 + C_n04х4² – b_n0  0, (8.13)

C_n10x0^2.7 + C_n12x2ⁿ³ – 3,2x4² –b_n1  0;

нелинейные равенства cneq(x0,…,x4) = 0:

Ce_n00x0² + Ce_n01x1² + 0,5x2² – Ce_n 13x3²  be_n0= 0, (8.14)

Ce_n10x0^1.3 + Ce_n11x1² – 1.4x2ⁿ⁴ + Ce_n13x1x2x3+ Ce_n14х2х3х4 ⁿ⁵  be_n1 = 0.

8.6.1. Представьте в РДМ исходные данные (8.7)…(8.12) в векторно-матричном виде (см. рис. 11.3 Пособия, формулы (11.8)…(11.15)), в частности, целевую функцию - в виде (11.11), используя поясняющие формулы (11.17)…(11.21) при формировании матрицы h для цельфункции, а нелинейные ограничения (8.11) и (8.12) перепишите в РДМ с использованием компонент введенного оптимизационного вектора х.

8.6.2. Ниже векторно-матричного представления:

• сформируйте максимизатор, аналогичный показанному на рис. 11.3 Пособия (но без ограничений – неравенств и равенств), с выводом вектора о3 и цельфункции у17(о3);

• скопируйте все векторные, векторно-матричные и нелинейные ограничения, соответствующие ограничениям (8.8)…(8.12) и вставьте их ниже максимизаторной функции;

• сформируйте аналогичный максимизатору минимизатор (путем копирования максимизатора) с заменой о3 на о4 и с выводом вектора о4 и функции у17(о4).

8.6.3. Вставьте в ваш Уорд-файл «Фамилия-MCad-D.doc» пункт «Текущая дата. Вычисление максимума (минимума) квадратичной целевой функции».

В этом пункте сформируйте таблицу, аналогичную табл. 8.2, с тем же названием, графы 6…9 которой заполните результатами расчетов х_опт и у17(х_опт) первого и второго оптимизаторов из п. 8.3.2..

8.6.4. Найдите оптимальные значения х и у17(х) для задач с сочетанием ограничений согласно табл. 8.2 («+» – ограничение есть, «–» – ограничение отсутствует), путем втаскивания в операционный блок мышкой или удаления из него блоков испытуемых ограничений. При отсутствии решения в соответствующие ячейки таблицы вставьте фразу «Нет решения».

Таблица 8.2