Текущая дата. Решение дифференциальных уравнений.

5.1. Решение дифуравнения n-го порядка замкнутой сау при единичном скачке задающего воздействия решателем odesolve(…). Вариант №___»

• Ознакомьтесь с правилами применения функции odesolve и разд. 7.1.1. «Построение переходного процесса в САУ».

• Постройте эталонный переходный процесс на единичный скачок задающего воздействия g(t) в САУ с дифуравнением замкнутой системы

Q(p) x(t) = R(p) g(t), p = d / dt. (5.1)

Вид уравнения и значения параметров – в данных к заданию 5 для вашего варианта: разд. 15.8 табл. 15.8.1.

• Вычислите измененные начальные условия по формулам (7.12), руководствуясь примером построения переходного процесса в разд. 7.1.1.2., и постройте переходный процесс по этапам, представленным на рис. 7.3 Пособия или рис. 5.1.

, p = d / dt. (5.2)

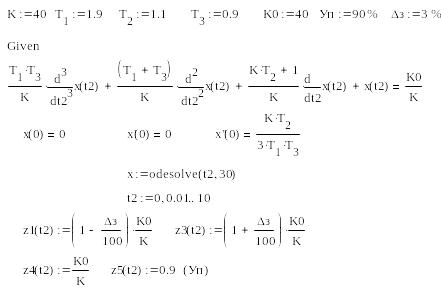
Рис. 5.1. Ввод данных в РДМ для построения эталонного переходного процесса и

вспомогательных измерительных линий (з = 3%, Уп = 90%) для САУ с уравнением (5.2)

• Постройте вспомогательные линии на графике переходного процесса и измерьте показатели качества переходного процесса (см. рис. 5.1 и 5.2) посредством измерителя Trace (в режиме сканирования по точкам графика), сведя их в таблицу, аналогичную табл. 5.1, построенную в созданном разделе Word-файла.

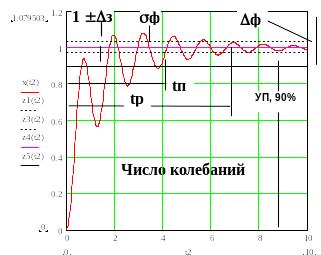
Рис. 5.2. Переходный процесс в САУ с уравнением (5.2) и показатели его качества: время подъема – tп до уровня Уп, время регулирования – tp (вхождение процесса в зону заданной статической погрешности з), фактическое перерегулирование ф, число колебаний на отрезке tp, фактическая статическая погрешность ф = 1 – х(t2= ).

• Скопируйте график переходного процесса, расположив его выше таблицы. Озаглавьте таблицу и график, аналогично соответствующим объектам из этого задания.

Таблица 5.1

Показатели качества переходного процесса в сау с уравнением (5.2)

Заданные		Измеренные
з, %	Уп,%	tп, с	tp, с	ф, %	np	ф
3	90	3,9	6,44	7,95	5,5	0

5.2. Вставьте в РДМ текстовый блок « 5.2. Текущая дата. Решение дифуравнения n-го порядка замкнутой САУ при единичном скачке задающего воздействия функцией rkfixed».

Постройте переходный процесс в САУ с дифуравнением замкнутой системы (5.1), взятым из п. 5.1 задания, руководствуясь этапами разд. 7.2.1 и рис. 7.4. Пособия.

5.3. Вставьте в рабочий документ текстовый блок « 5.3. Текущая дата. Решение дифуравнения/системы дифуравнений 1-го порядка (в зависимости от вашего варианта). Кривая (название), вариант №___».

• Решите дифуравнение или систему дифуравнений решателем rkfixed(…) при начальных условиях: и данных вашего варианта из табл. 15.8.2 разд. 15.8, используя разд. 7.2.1 и 7.2.2 Пособия.

• Постройте график решения в координатах, руководствуясь графой 7 табл. 15.8.2 и соответствующим рисунком (при его наличии), снабдите график поясняющей надписью.

• Скопируйте решение и график, установите параметры классической кривой (в конце каждого раздела табл. 15.8.2, за исключением двух последних), проконтролируйте изменение графика.

5.4. Вставьте в рабочий документ текстовый блок « 5.4. Текущая дата. Решение линейной системы дифуравнений 1-го порядка надежности САУ. Вариант №___».

Решите систему дифуравнений (описывает надежность работы ремонтируемой резервированной САУ) решателем rkfixed(…) при начальных и нормировочном условиях и данных вашего варианта из табл. 15.8.3, используя разд. 7.2.4 Пособия и рис. 5.3 настоящего задания.

• Постройте график решения в координатах, руководствуясь рис. 5.3, снабдите график аналогичными поясняющими надписями.

Обратите внимание на способ ввода нормировочного условия – рис. 5.3 и 5.4.

• Постройте таблицу вычисленных нормированных вероятностей, руководствуясь командами рис. 5.4.

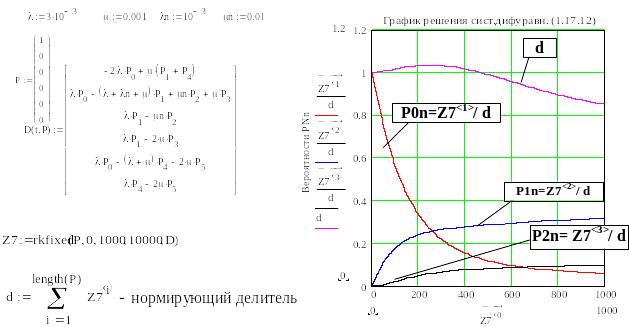
(5.3)

Рис. 5.3. Решение системы шести дифуравнений. На рисунке – графики первых трех нормированных вероятностей: P0n, P1n и P2n (в РД Mathcad рисунок должен располагаться ниже присвоения d).

Нормировочное условие в случае системы (5.3):

Р₀(t) + Р₁(t) + Р₂(t) + Р₃(t) + Р₄(t) + Р₅(t) = 1, (5.4)

поэтому нормированное значение вероятности, например, Р₀ – Р0n, равно

Р0n(t) = P₀(t) / ( Р₀(t) + Р₁(t) + Р₂(t) + Р₃(t) + Р₄(t) + Р₅(t) ) = Z7^<1>/d. (5.5)

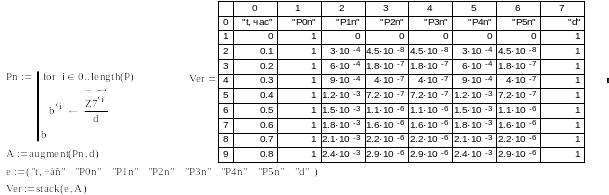
Рис. 5.4. Вывод таблицы нормированных вероятностей решения системы (5.3)

Задание 6

Решение линейных дифференциальных уравнений и систем методом прямого и обратного преобразования Лапласа. Исследование систем автоматического управления с периодической нелинейностью на границе устойчивости «в большом»

1. Создайте новый рабочий документ в Mathcad для 6-го…8-го заданий, сохранив его в вашей папке под именем «Р6−8МкдФамилия(ваша)».

2. Вставьте в РДМ текстовый блок:

«Задание 6