4.1. Текущая дата. Решение системы линейных уравнений посредством функции lsolve(m,V). Вариант №___»

4.3. Решите систему линейных (7) уравнений посредством функции Mathcad lsolve(M,v), вызвав её из меню f(x):

a11х1 +a12х2+a13х3 +a14х4 +a15х5 = b1,

a21х1 +a22х2+a23х3 +a24х4 +a25х5 = b2,

a31х1 +a32х2+a33х3 +a34х4 +a35х5 = b3, (4.1)

a41х1 +a42х2+a43х3 +a44х4 +a45х5 = b4,

a51х1 +a52х2+a53х3 +a54х4 +a55х5 = b5,

Выполните в рабочем документе действия, согласно примеру разд. 6.1 Пособия. Вариант ваших коэффициентов и правых частей уравнения (4.1) – в Данных к заданию 4 разд. 15.6, табл. 15.6.1.

4.4. Вставьте в рабочий документ п. «4.2. Индивидуальное решение системы нелинейных уравнений. Вариант №___». Решите систему нелинейных уравнений (4.2) вашего варианта (см. Исходные данные – разд. 15.7, табл. 15.7.1) посредством решателя Mathcad Given … Find:

f1(x, y)= 0,

f2(x, y)= 0.

Используйте пример рис. 4.1 или 4.2 Задания 4.

Внимание! Решатель Given … Find является локальным оператором: он вычисляет корни системы, соответствующие начальному приближению, и не производит какого-либо поиска дополнительных корней. Чтобы вычислить заданное число корней, нужно для каждого корня найти его приближенное значение посредством упрощенного решения системы с использованием графических средств Mathcad.

Различают два варианта при графическом упрощенном решении системы: когда переменные в уравнении системы можно отделить друг от друга и когда нельзя.

1. Для первого варианта в каждом уравнении одну из неизвестных выражают через другую, строят две кривые на графике, точки пересечения которых и дают приближенные значения корней, которые затем уточняют посредством решателя Given-Find – см. рис. 4.1. Приближенные значения измеряют посредством панельки Trace (щелчок ПКМ на графике-Контекстное меню-Trace).

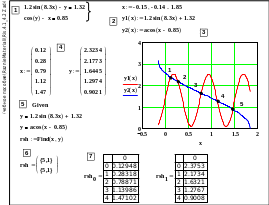
(4.3)

Рис. 4.1. Решение системы уравнений (4.3) с отделяющимися неизвестными (показаны 5 корней системы). 1–исходная система; 2–система с разделенными переменными для построения графика 3; 4–векторы приближенных значений координат корней, определенных через измеритель «X-Y Trace»; 5–решатель системы (4.3); 6–выходная таблица решателя в виде гнездовой матрицы; 7– вывод элементов гнездовой матрицы–координат х и у корней

2. Для второго варианта одну переменную выражают через другую, используя локальный решатель root(…), строят кривые, находят точки пересечения и далее действуют аналогично первому случаю – см. рис. 4.2. Как видно из этапов 4…7, решатель находит корни, отличающиеся от начальных приближений (векторы

(4.4)

Рис. 4.2. Решение системы уравнений (4.4) с неотделяющимися переменными (показаны 4 корня) системы. Этап 8 – Индивидуальное вычисление корней в точках 1…4 решателем 5: хн, ун – начальные координаты корня, хк, ук – координаты корня, вычисленные решателем

х и у в этапе 4) и лежащие вне исследуемого диапазона (0,01…1,5). Поэтому корни в точках 1…4 графика вычислялись индивидуально на этапе 8: хн, ун – начальные координаты корня (определенные посредством панельки Trace ), хк, ук – координаты корня, вычисленные решателем из этапа 5.

4.5. Вставьте в рабочий документ п. «4.4. Полное сеансовое решение системы 2 нелинейных уравнений методом сканирования по начальным данным с контролем вычисляемых корней по контурной карте системы, Вар.№ (ваш вариант)».

1. Ознакомьтесь с Решением системы нелинейных уравнений Методом сканирование по начальным данным с решателем given-find по разд. 6.3.1 Пособия.

2. Постройте контурную карту заданной системы уравнений согласно Этапам формирования контурной карты разд. 6.3.1.3 и рис. 6.9; нанесите границы области поиска корней и номера всех точек взаимопересечения разноименных контуров, как кандидатов на корни. Если количество определяемых корней больше 30, то их число можно уменьшить в пределах области поиска до 30 с обязательным изменением границ области.

3. Сформируйте решатель системы уравнений, аналогичный рис. 6.7, А, и произведите одно успешное сканирование области поиска корней по неизвестной х для у, равной середине её диапазона.

4. Сформируйте управляющие объекты Суперрешателя системы уравнений согласно разд. 6.3.1.1 Ввод объектов решающей структуры, рис. 6.8 и табл. 6.1. В процессе отладки объектов используйте найденные в пробном сеансе в п.3 корни, отсеяв вручную внешние корни в таблицах kxr и kyr после вставки в них корней сеанса.

5. Проведите поиск всех корней системы уравнений в заданной области согласно методике разд. 6.3.1.2, заполняя и обновляя соответствующие таблицы Суперрешателя, включая и протокол ПРСУ (табл. 6.1), управляя процессом сканирования посредством контроля количества найденных корней (не отображая их на Контурной карте). Сканирование следует прекратить, когда сеансы перестанут давать новые корни.

6. Создайте формирователь координат корней для контурной карты по результатам сеансов из п. 5 согласно Этапам построения группы корней на контурной карте и рис. 6.10, А, обеспечив выведение всех сеансовых корней на контурную карту, аналогично рис. 6.10, Г.

7. Проанализируйте полученную картину в п. 6, и если есть возможность вычислить новые корни сканированием, произведите сеансы сканирования. Полученными новыми корнями обновите таблицы и протокол Суперрешателя, Контурную карту.

8. Если на Карте остались не вычисленные корни, то следует приступить к индивидуальному вычислению каждого корня с заполнением табл. 6.2 и протокола ПРСУ (фильтры и остальные управляющие объекты Суперрешателя использовать не нужно). Индивидуальной проверке должны быть подвергнуты все неотсканированные корни.

9. Если в п. 8 были найдены новые корни, то их следует вывести на Контурную карту в формате, отличном от ранее выведенных корней (по форме и цвету знака корня), используя п. 4 Этапов построения группы корней… и рис. 6.10, В.

4.6. Вставьте в рабочий документ п. «4.5. Зависимость решения системы нелинейных уравнений от параметра». Исследуйте зависимость решения системы нелинейных (4.5) уравнений от параметров “а” и “b”:

________________________ f3(x,y,а)________________________________ = 0,

(4.5)

________________________ f4(x,y,b)________________________________ = 0.

Используйте пример рис. 6.5 Пособия

• В качестве системы (4.5) возьмите систему (4.2) и введите в нее параметры, как показано в (4.5) в любое место каждого уравнения.

• Задайте каждому параметру по 2 значения и проконтролируйте по графику, чтобы система была совместна при всех сочетаниях значений.

• Введите в РДМ объекты, аналогичные рис. 6.5, и запустите вычисления.

• Постройте итоговую таблицу расчета, аналогичную рис. 6.6 Пособия, используя программный комплекс ИТР2 и этапы построения, представленные на рис. 6.6.

Задание 5

Решение обыкновенных дифференциальных уравнений и систем (задача Коши). Переходные процессы в САУ и показатели качества. Решение систем дифференциальных уравнений надежности систем автоматического управления

. Вставьте в РДМ раздел и пункт:

«Задание 5