«Задание 2

2.1. Текущая дата. Вычисления по формуле с комплексными числами. Исследование устойчивости сау. Вариант №___»

По передаточной функции разомкнутой системы (данные возьмите для вашего варианта из табл. 15.1.2 разд. 15.1)

(2.1)

исследуйте устойчивость САУ, согласно разд. 2.6.2 Пособия, меняя величину К.

• Постройте показательную точку (–1, i0) и два годографа: один – устойчивый, причем запас устойчивости по амплитуде  (см. рис. 2.8, В) у него должен быть не более 4 % (для определения запаса используйте измеритель «X-Y Trace» в режиме сканирования по точкам графика: при выделенном графике –Формат-Граф-Трейс; измеренное значение х должно находиться в промежутке –1…–0,96); другой – неустойчивый, по вашему усмотрению (см. исходные формулы (2.9) и построения на рис. 2.8. Пособия).

• По измеренному х (измерения производите на увеличенном участке графика, аналогичном рис. 2.1) вычислите запас устойчивости  по формуле (2.2) и вставьте наименование единицы измерения – %.

( 2.2)

Рис. 2.1. Определение исходных данных х и х для вычисления запасов

устойчивости по амплитуде  и фазе  для САУ с

• Н 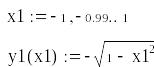а вашем графике постройте также нижнюю полуокружность единичного радиуса y1(x1), используя формулы (2.3) – см. рис. 2.1.

(2.3)

• По точке пересечения полуокружности с устойчивым годографом W(w,К) посредством X-Y-Trace измерьте x (см. рис. 2.1) и вычислите запас устойчивости по фазе  посредством формулы (2.4) вставьте наименование единицы измерения – град.

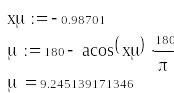
(2.4)

, град

3. Вставьте новый пункт «2.2. Текущая дата. Решение уравнений. 2.2.1. Полиномиальное уравнение. Вариант №___». Решите уравнение (2.5), используя оператор polyroots(v), согласно разд. 5.1.1 Пособия.

а6х⁶ + а5х⁵ + а4х⁴ + а3х³ + а2х² + а1х + а0 = 0. (2.5)

Данные, согласно вашему варианту, – в разд. 15.4 Пособия (табл. 15.4.1).

4. Вставьте новый пункт «2.2.2. Текущая дата. Исследование уравнения. Вариант №___». Проведите исследование уравнения (2.6) (т.е. определите зависимость корней уравнения от векторных параметров р1 и р2 при квазирядном способе сочетания их значений) на основе методики разд. 5.1.3, рис. 5.4 с формированием полной таблицы ИТИ.

Р4а4х⁴ + Р3а3х³ + Р2а2х² + Р1а1х + Р0а0 = 0 (2.6)

Данные к уравнению, согласно вашему варианту, – в разд.15.4 Пособия (табл. 15.4.2 и 15.4.3), причем, коэффициенты выражаются через параметры р1и р2 с использованием численных значений Р4…Р0 и табл. 15.4.2. Озаглавьте полученную таблицу.

5. Вставьте новый пункт «2.2.3. Текущая дата. Определение погрешности вычисления корней полиноми­аль­ного уравнения»

Используя методику программного построения таблицы погрешностей вектора корней из рис.5.6 разд. 5.1.4, вычислите погрешности и невязки для вектора корней из п.2.3. Озаглавьте полученную таблицу.

2.6. Вставьте новый пункт «2.2.4. Текущая дата. Уточнение вектора вещественных корней вычислителем дихутчкор(у,,шфио)». Вычислите уточненные значения корней из п. 2.3, используя методику рис. 5.7 разд. 5.1.5. Озаглавьте полученную таблицу.

Если уравнение (2.5) не имеет вещественных корней, то п. 2.6. выполнять не надо.