Адсорбция на границе «жидкость – газ». Уравнение Ленгмюра

Изотерма адсорбции Ленгмюра для раздела "жидкость – газ" и "жидкость – жидкость" имеет вид, приведенный на рисунке 71.

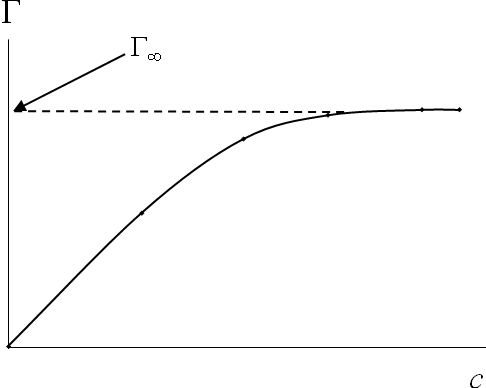
Рис. 71. Изотерма адсорбции Ленгмюра

Наибольшее и постоянное значение адсорбции Г, при котором достигается насыщение адсорбционного слоя и адсорбция уже не зависит концентрации, называют предельной адсорбцией Г_. При больших концентрациях поверхностный слой насыщен молекулами растворенного вещества.

Для приближенных расчетов производную d/dc в уравнении Гиббса для адсорбции (310) можно заменить на

.

(312)

Для объяснения зависимости адсорбции как на легкоподвижных границах, так и на границах с твердыми фазами И. Ленгмюр в 1915 г. предложил теорию мономолекулярной адсорбции. Уравнение мономолекулярной адсорбции для границы газ – жидкость имеет вид:

,

(313)

где Г_ – предельная адсорбция в мономолекулярном слое (Г  Г_ при с  ); K – константа адсорбционного равновесия.

Величина константы равновесия адсорбции тем больше, чем сильнее выражено сродство данного адсорбируемого вещества к данному адсорбенту или чем больше работа адсорбции вещества на межфазной границе. Помимо природы адсорбента и адсорбата на величину K влияет температура. С повышением температуры усиливается процесс десорбции, так как возрастает кинетическая энергия молекул адсорбата и константа K уменьшается. Уравнение Ленгмюра (313) выражает зависимость адсорбции от равновесной концентрации вещества в объеме раствора при постоянной температуре и носят название уравнений изотермы адсорбции Ленгмюра. Помимо константы K в уравнение Ленгмюра входит постоянная Г_, которая представляет собой предельное значение адсорбции. Величина Г_ зависит от размеров молекул адсорбата. Очевидно, что чем крупнее молекула адсорбата, тем больше площадь, приходящаяся на молекулу в адсорбционном слое, и тем меньше величина Г_. Ее выражают числом молей адсорбата на единицу площади (моль/м²).

На изотерме адсорбции (рис. 71) можно выделить три участка: начальный, промежуточный и горизонтальный, идущий параллельно оси абсцисс.

Анализ уравнения Ленгмюра показывает, что в зависимости от концентрации адсорбата оно может принимать различный вид. При малых концентрациях, когда Kc << 1, этой величиной в знаменателе можно пренебречь и уравнение принимает вид

.

(314)

При больших концентрациях, когда Kc >> 1, можно пренебречь единицей в знаменателе уравнения Ленгмюра (313), тогда Г = Г_.

Для графического определения величин K и Г_ используют линейную форму уравнения Ленгмюра (315). Для линеаризации уравнения (313) найдем обратные величины от левой и правой части этого уравнения:

.

Разделим слагаемые в числителе правой части на знаменатель и проведем сокращения:

.

(315)

Уравнение (315) имеет линейный вид у = ах+b, где

, , , .

График в координатах представляет собой прямую (рис. 72). Ордината точки, получаемой при экстраполяции прямой до вертикальной прямой при с = 0, равна 1/Г_.

Константа адсорбционного равновесия K рассчитывается по графику (рис. 72): методом экстраполяции при х = 0 определяем коэффициент b в уравнении прямой y=ax+b. Используя координаты y₁ и x₁ точки 1, лежащей на прямой, рассчитываем коэффициент а по формуле (316):

.

(316)

Рис. 72. Графическое определение констант уравнения адсорбции Ленгмюра

Степенью заполнения поверхности адсорбатом называют величину

.

(317)

Степень заполнения показывает, какая доля поверхности занята молекулами адсорбата.