Примеры решения задач
1. Определить методом подстановки порядок и константу скорости реакции A … по зависимости концентрации реагента от времени, прошедшего с момента начала реакции. Температура 298 К.
№ |
t, c |
cA, М |
|
№ |
t, c |
cA, М |
1 |
0 |
0,180 |
|
6 |
500 |
0,0346 |
2 |
100 |
0,128 |
|
7 |
600 |
0,0249 |
3 |
200 |
0,0929 |
|
8 |
700 |
0,0177 |
4 |
300 |
0,0681 |
|
9 |
800 |
0,0129 |
5 |
400 |
0,0474 |
|
10 |
900 |
0,0092 |
Решение:
Рассчитаем константу скорости изучаемой реакции в предположении, что это реакция 0-го, 1-го и 2-го порядка по уравнениям (259), (264) и (268). Анализ рассчитанных значений констант показывает, что постоянные значения константы получаются при выборе уравнения (264) для реакции 1 порядка. Из графика видно, что ее значения случайно колеблются около некоторого среднего значения. Следовательно, исследуемая реакция имеет 1-й порядок по веществу А. Среднее значение константы скорости равно 0,00331 с–1.
№ |
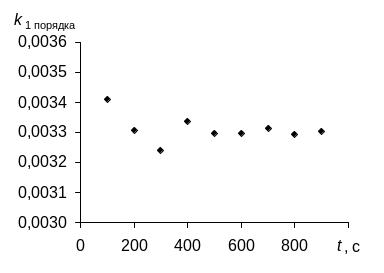
t, c |
cA, М |
Константа для реакции |
||
0 порядка |
1 порядка |
2 порядка |
|||
1 |
0 |
0,180 |
– |
– |
– |
2 |
100 |
0,128 |
0,000520 |
0,00341 |
0,0226 |
3 |
200 |
0,0929 |
0,000436 |
0,00331 |
0,0260 |
4 |
300 |
0,0681 |
0,000373 |
0,00324 |
0,0304 |
5 |
400 |
0,0474 |
0,000332 |
0,00334 |
0,0389 |
6 |
500 |
0,0346 |
0,000291 |
0,00330 |
0,0467 |
7 |
600 |
0,0249 |
0,000259 |
0,00330 |
0,0577 |
8 |
700 |
0,0177 |
0,000232 |
0,00331 |
0,0728 |
9 |
800 |
0,0129 |
0,000209 |
0,00330 |
0,0900 |
10 |
900 |
0,0092 |
0,000190 |
0,00330 |
0,1146 |
Среднее значение константы, с–1 |
|
0,00331 |
|
||
2. Определить графическим методом порядок и константу скорости реакции A … по зависимости концентрации реагента от времени, прошедшего с момента начала реакции. Температура 298 К.
№ |
t, c |
cA, М |
|
№ |
t, c |
cA, М |
1 |
0 |
0,180 |
|
6 |
500 |
0,0273 |
2 |
100 |
0,0907 |
|
7 |
600 |
0,0241 |
3 |
200 |
0,0590 |
|
8 |
700 |
0,0206 |
4 |
300 |
0,0408 |
|
9 |
800 |
0,0193 |
5 |
400 |
0,0328 |
|
10 |
900 |
0,0162 |
Решение:
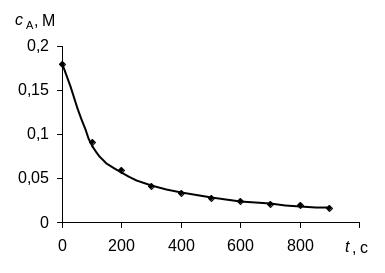
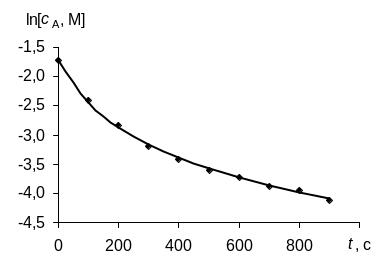
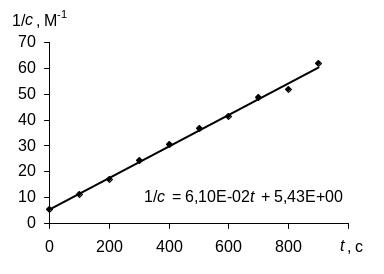
Для определения порядка реакции этим методом рассчитаем по экспериментальным данным значения ln с, 1/с и построим графики зависимостей "с – t", "ln с – t", "1/с – t", в которых линеаризуются кинетические уравнения (258), (262) и (267) реакций 0-го, 1-го и 2-го порядков соответственно.
№ |
t, c |
cA, М |
ln [с, М] |
1/с, М–1 |
1 |
0 |
0,180 |
–1,715 |
5,56 |
2 |
100 |
0,0907 |
–2,400 |
11,0 |
3 |
200 |
0,0590 |
–2,830 |
16,9 |
4 |
300 |
0,0408 |
–3,199 |
24,5 |
5 |
400 |
0,0328 |
–3,417 |
30,5 |
6 |
500 |
0,0273 |
–3,601 |
36,6 |
7 |
600 |
0,0241 |
–3,726 |
41,5 |
8 |
700 |
0,0206 |
–3,882 |
48,5 |
9 |
800 |
0,0193 |
–3,948 |
51,8 |
10 |
900 |
0,0162 |
–4,123 |
61,7 |
Зависимость для изучаемой реакции является прямолинейной, если использовать уравнение (267), выведенное для кинетики 2-го порядка. Следовательно, изучаемая реакция является реакцией второго порядка по реагенту А.
|
|
|
|
|
|
|
|
Константа скорости реакции в соответствии с уравнением (267) равна коэффициенту наклона 6,1010–2 л/(мольс) в уравнении прямой, которое найдено методом наименьших квадратов.
3. Определить порядок и константу скорости реакции A … по времени полупревращения, используя экспериментальные данные, полученные при 298 К
с0А, М |
t1/2, с |
0,0317 |
26,9 |
0,0528 |
44,8 |
0,0916 |
81,5 |
0,134 |
115 |
0,294 |
264 |
0,403 |
335 |
Решение:
Анализ экспериментальной зависимости времени полупревращения от начальной концентрации реагента А (таблица) позволяет из уравнений (260), (265) и (269)
, , ,
сразу отбросить второе (так как в соответствии с этим уравнением время полупревращения должно быть постоянным, а, судя по таблице, оно не постоянно) и третье уравнение (так как в соответствии с этим уравнением время полупревращения должно уменьшаться с увеличением начальной концентрации реагента, а оно увеличивается).
Остается первое уравнение, выведенное для кинетики 0-го порядка, однако необходимо проверить, действительно ли время полупревращения реагента А, найденное в эксперименте, прямо пропорционально начальной концентрации реагента. Для этого построим график зависимости в координатах "t1/2 – c0". Если в этих координатах зависимость будет иметь вид прямой, проходящей через начало координат, как и график уравнения (260), то это будет являться подтверждением того, что исследуемая реакция является реакцией 0-го порядка.
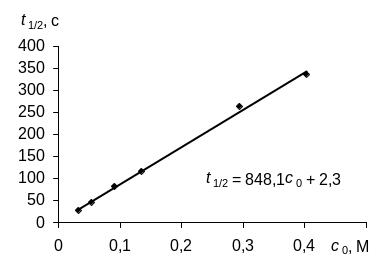
Прямолинейность графика и малая величина отрезка, отсекаемого на оси ординат при t1/2 = 0 (2,3), подтверждают вывод о том, что исследуемая реакция имеет 0-ой порядок по реагенту А.
Константу скорости реакции находят из уравнения (260), которое, если выделить коэффициент перед начальной концентрацией, примет вид:
.
Расчет коэффициентов прямой (t1/2 = 848,1с0 + 2,3), выполненный по методу наименьших квадратов, приводит к ненулевому значению ординаты при с0 = 0 (t1/2 = 2,3). Этим отличием от нуля, которое возникает из-за ошибок, допущенных в эксперименте в определении времени и концентраций, в нашем случае можно пренебречь, так как ошибка в определении этого коэффициента прямой больше самого значения коэффициента (подробности расчета здесь не приводим).
Таким образом
и значение константы скорости равно
.
4. Монохлоруксусная кислота при температуре 298 К гидролизуется (вода в большом избытке)
CH2ClCOOH + H2O CH2OHCOOH + HCl
Были проведены четыре эксперимента, в которых измерялась концентрация монохлоруксусной кислоты от времени (начальная концентрация кислоты была различна)
t, мин |
0 |
200 |
600 |
780 |
c1, М |
0,129 |
0,119 |
0,101 |
0,0925 |
c2, М |
0,0867 |
0,0787 |
0,0669 |
0,0616 |
c3, М |
0,0508 |
0,0466 |
0,0396 |
0,0363 |
c4, М |
0,0259 |
0,0237 |
0,0200 |
0,0186 |
Методом Вант-Гоффа определить порядок реакции и рассчитать кажущуюся константу скорости реакции.
Решение:
Так как вода взята в большом избытке, то можно применить метод Вант-Гоффа. Скорость реакции равна (А – монохлоруксусная кислота)
По первым двум колонкам таблицы рассчитаем значения средних скоростей реакции (уравнение (252)) и соответствующие им средние значения концентраций (уравнение (253)), а также их натуральные логарифмы (в точных расчетах используют средние значения концентраций по времени; в ориентировочных эту величину можно заменить средней по концентрации).
cсред |
сред |
ln cсред |
ln сред |
0,124 |
0,0000500 |
–2,087 |
–9,903 |
0,0827 |
0,0000400 |
–2,493 |
–10,127 |
0,0487 |
0,0000210 |
–3,022 |
–10,771 |
0,0248 |
0,0000110 |
–3,697 |
–11,418 |
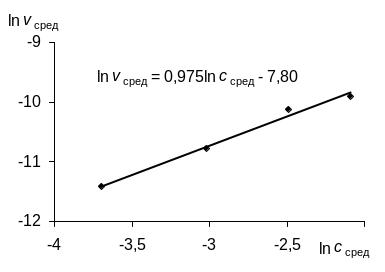
Для нахождения порядка и константы скорости реакции по коэффициентам уравнения (273) строим график в координатах "ln – ln cA".
Угловой коэффициент уравнения рассчитанный по графику (рисунок) близок к 1; из этого следует, что порядок реакции по монохлоруксусной кислоте близок к 1, а кажущаяся константа скорости в уравнении (272) равна
