Задачи для самостоятельного решения

1. Для реакции I₂ (;( 2I приводятся константы равновесия при нескольких температурах:

Т, К	950	1050	1150	1250
Kр103	1,134	7,316	33,83	127,1

Постройте график зависимости lnK_р от 1/Т и определите реакции.

(Ответ: 150,0 кДж)

2. Для реакции C₆H₆(г) + 3H₂ (;( C₆H₁₂ (г) зависимость константы равновесия от температуры выражается уравнением

Выведите уравнение зависимости в этой реакции от температуры и рассчитайте .

(Ответ: –204,3 кДж)

3. Для реакции SO₂ + ¹/₂O₂ (;( SO₃ константа равновесия K_р при 900 К равна 0,04310^–2, а при 950 К – 1,06210^–2. Определите K_р при 930 К. Примите, что тепловой эффект в температурном диапазоне 900 – 950 К постоянен.

(Ответ: K_p = 3,110^–3)

4. Для реакции цис-C₅H₁₀(г) + 2H₂ (;( C₃H₈(г) + C₂H₆(г) протекающей в газовой фазе, при температуре 750 К известна константа равновесия K_р = 3,343 атм^–1. Рассчитайте выход продуктов, если давление равно 5 атм, исходное количество циклопентана равно 1,2 моль, а водорода – 2,4 моль.

(Ответ: 73,6%)

Модуль 2 химическое равновесие. Фазовые равновесия

1.3. Термодинамика фазовых равновесий

Раздел "Термодинамика фазовых равновесий" имеет непосредственное отношение к прогнозированию состояния индивидуальных лекарственных веществ и их смесей. Теория фазовых равновесий позволяет выявлять случаи физико-химической несовместимости фармацевтических препаратов. Термодинамические методы используются для теоретического описания и практических расчетов таких широко распространенных процессов разделения и очистки многокомпонентных смесей, как простая перегонка и ректификация, перегонка с водяным паром и экстракция. Закономерности, изучаемые в данном разделе, позволяют обоснованно выбирать оптимальные условия проведения перечисленных процессов, при которых достигается наилучшее качество фармацевтических препаратов.

1.3.1. Фазовые равновесия в однокомпонентных системах. Правило фаз Гиббса. Уравнения Клапейрона, Клапейрона – Клаузиуса Основные уравнения

Термодинамическая система – это тело или группа тел, находящихся во взаимодействии и условно обособленных от окружающей среды.

Система называется гомогенной, если она состоит из одной фазы. Система называется гетерогенной, если она состоит из двух или более фаз.

Фазой называется совокупность однородных частей системы (т.е. одинаковых по физическим, химическим и термодинамическим свойствам), отделенная от других частей системы физической (реально существующей) поверхностью раздела. Индивидуальное вещество в твердом агрегатном состоянии всегда образует самостоятельную фазу.

Жидкие и твердые фазы называются конденсированными.

Если вещество содержится одновременно в разных фазах, то происходит его переход из одной фазы в другую, такой переход называется фазовым. Состояние, при котором скорости противоположных фазовых переходов равны, называется фазовым равновесием.

Компонентами (составляющими веществами) называются все химические вещества, которые могут быть выделены из системы и существовать вне ее.

Число степеней свободы – это число интенсивных термодинамических параметров, которые можно произвольно менять в некоторых пределах, чтобы не изменилось число и природа фаз в системе.

Расчет числа C в равновесной системе в зависимости от числа компонентов K, числа фаз Ф и от числа термодинамических параметров n, которые отличаются от химических потенциалов, (в подсчете участвуют параметры р и Т) производят с помощью правила фаз Гиббса (1876):

С = K – Ф + n.

(135)

Если из внешних параметров на систему оказывают влияние p и T, то n = 2 и правило фаз принимает вид

С = K – Ф + 2

(136)

Если из внешних параметров на систему оказывает влияние только температура, а давление постоянно (или наоборот), то правило фаз принимает вид

С = K – Ф + 1

(137)

Для однокомпонентных систем, примером которых является система, образованная водой, как компонентом,

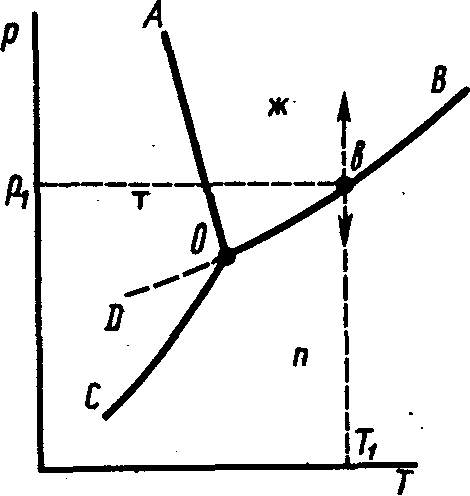
Рис. 40. Диаграмма состояния воды

правило фаз (135) принимает вид

С = 1 – Ф + 2 = 3 – Ф,

(138)

Если минимальное число степеней свободы (С_min) равно нулю (система инвариантна), то, согласно (138), Ф = 3. В равновесной однокомпонентной системе могут сосуществовать максимально три фазы (т, ж, г). Максимальным числом степеней свободы (С_max) система обладает при Ф_min, которое не может быть меньше единицы. Следовательно, С_max= 1 – 1 + 2 = 2. Этими степенями свободы являются давление и температура.

На диаграмме состояния воды имеются три поля: льда (т), жидкости (ж) и пара (п). В пределах каждого поля можно произвольно менять температуру и давление без изменения числа фаз, так как при Ф = 1 число степеней свободы

С = 1 – 1 + 2 = 2.

Кривые АО, ВО и СО характеризуют те значения р и Т, при которых в системе имеются в равновесии две фазы. Каждая из кривых показывает зависимость температуры фазового перехода от внешнего давления.

Система, заданная точкой на любой кривой, моновариантна, то есть имеет одну степень свободы (С = 3 – 2 = 1). Следовательно, произвольно можно изменять или давление, или температуру. Второй параметр изменяется в зависимости от первого. Например, при выбранной температуре T₁ (рис. 40) равновесие ж (;( п может существовать только при давлении р₁ (точка b). Если при Т₁ произвольно изменить давление, то система из двухфазной перейдет в однофазную.

Точка О на диаграмме соответствует системе, в которой существуют три фазы (т, ж, п). В этом случае С = 1 – 3 + 2 = 0 (система инвариантна). В таком состоянии система может находиться при t = 0,0076 °С и давлении 610 Па. Точку О называют тройной точкой воды. Даже небольшое изменение одного из параметров нарушает равновесие и приводит к исчезновению одной или двух фаз.

Уравнение Клапейрона (1834) связывает между собой давление, при котором происходит фазовый переход, и температуру фазового перехода. Для процесса испарения воды в дифференциальной форме оно имеет вид

(139)

или

.

(140)

Позже оно было модифицировано Р.Клаузиусом (1836) для равновесий, в которых одна из фаз является паром: "жидкость" – "пар" и "твердая фаза" – "пар". В этом частном случае оно называется уравнением Клапейрона – Клаузиуса и в дифференциальной форме имеет вид

(141)

или

.

(142)

После перехода к интегральной форме уравнения Клапейрона – Клаузиуса оно позволяет рассчитывать значение давления, при котором устанавливается фазовое равновесие, в зависимости от температуры

,	(143)
,	(144)